A small block is shot into each of the four tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in
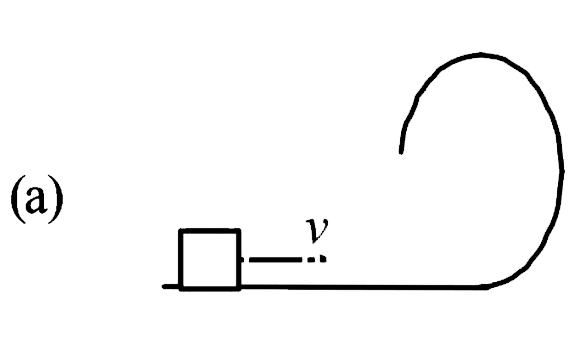
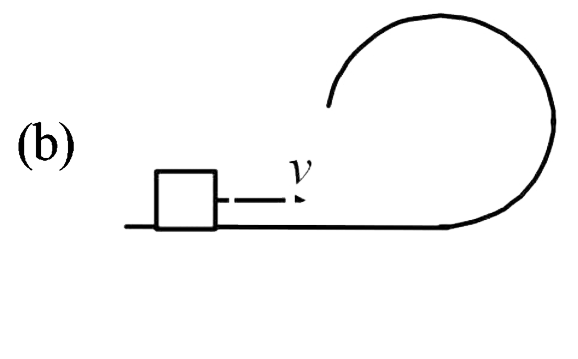
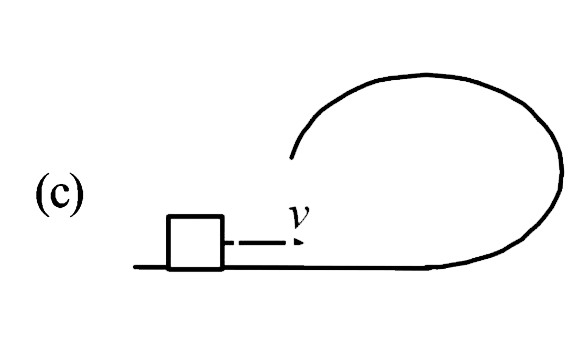
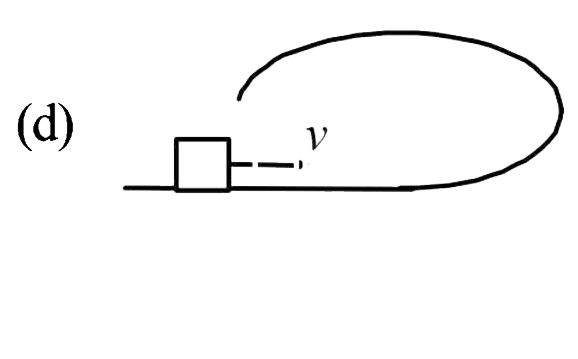
The correct Answer is:A
To solve the problem, we need to analyze the normal reaction force acting on a small block at the highest point of four different tracks. The normal reaction force R at the highest point can be expressed using the following equation:
R=mv2r−mg
Where:
- m is the mass of the block,
- v is the speed of the block at the highest point,
- r is the radius of curvature of the track at that point,
- g is the acceleration due to gravity.
1. Identify the Variables:
- We know that the speed v is the same for all tracks and that the height reached by the block is the same for all tracks.
2. Understand the Equation:
- The normal reaction R is dependent on the radius of curvature r. For R to be maximum, the term mv2r must be maximized, which means r must be minimized.
3. Analyze the Tracks:
- We need to determine which track has the smallest radius of curvature at the highest point. The smaller the radius, the larger the centripetal force component mv2r will be, thus increasing R.
4. Evaluate Each Track:
- Without the specific diagrams, we can generally state that if we have different shapes for the tracks, we should look for the one that has the sharpest curve at the topmost point.
- Typically, a circular or semi-circular path has a constant radius, while other shapes may have varying radii.
5. Determine the Track with Minimum Radius:
- After analyzing the shapes of the tracks, we find that Track A has the smallest radius of curvature at the highest point compared to the other tracks.
6. Conclusion:
- Since Track A has the minimum radius of curvature, the normal reaction force R will be maximum at the highest point of Track A.
Final Answer:
The normal reaction is maximum in Track A.
- m is the mass of the block,
- v is the speed of the block at the highest point,
- r is the radius of curvature of the track at that point,
- g is the acceleration due to gravity.
- We know that the speed v is the same for all tracks and that the height reached by the block is the same for all tracks.
- The normal reaction R is dependent on the radius of curvature r. For R to be maximum, the term mv2r must be maximized, which means r must be minimized.
- We need to determine which track has the smallest radius of curvature at the highest point. The smaller the radius, the larger the centripetal force component mv2r will be, thus increasing R.
- Without the specific diagrams, we can generally state that if we have different shapes for the tracks, we should look for the one that has the sharpest curve at the topmost point.
- Typically, a circular or semi-circular path has a constant radius, while other shapes may have varying radii.
- After analyzing the shapes of the tracks, we find that Track A has the smallest radius of curvature at the highest point compared to the other tracks.
- Since Track A has the minimum radius of curvature, the normal reaction force R will be maximum at the highest point of Track A.
The normal reaction is maximum in Track A.
Topper's Solved these Questions
- HEAT AND THERMODYNAMICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - HEAT AND THERMODYNAMICSEXERCISE - JEE Main And Advanced
219 Videos
- MECHANICAL PROPERTIES OF MATTER AND FLUIDSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MECHANICAL PROPERTIES OF MATTER AND FLUIDSEXERCISE - Subjective Problems
1 Videos
Similar Questions
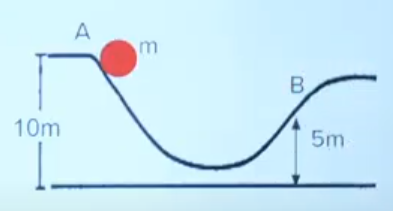
A body of mass 10kg is at height of 10m at point A as shown on a smooth track. Find speed at B.
View SolutionIn problem 17 if the mass m is allowed to fall from a height 2R, find the reaction of the track on the sliding mass the lowest point, at the highest point, at the mid-point. Take R:r=5:2
View Solution
Knowledge Check
A small block is projected into each of the four tracks as shown below. Each of the tracks rises to the same height. The speed with which the block enters the track is the same in all cases. At the highest point of the track, the normal reaction is maximum in
A B
B C
C D
D
A flexible track is fixed in two alternative arrangements, as shown in the figure. A toy car is released at rest and slides down the track air resistance can be ignored. The length of the track used is the same in each case and the height through which it falls from the bench to the floor is the same.


codes:APQRS1423BPQRS2312CPQRS3112DPQRS4132A flexible smooth track is fixed in two alternate arrangments, as shown in figure -1 and 2. the length of the track used is the same in each case, and the height through which it falls from the bench to the floor is the same. A toy car is released at rest and slides down the track. air resistance can be ignored.
 AThe speed at the bottom as well as time taken in both the traks are the same.BThe speed at the bottom as well as time taken in both the tracks are differentCThe speed at the bottom is different but the time taken in both the tracks are the same.DThe speed at the bottom is same but the time taken in both the tracks are different.
AThe speed at the bottom as well as time taken in both the traks are the same.BThe speed at the bottom as well as time taken in both the tracks are differentCThe speed at the bottom is different but the time taken in both the tracks are the same.DThe speed at the bottom is same but the time taken in both the tracks are different.
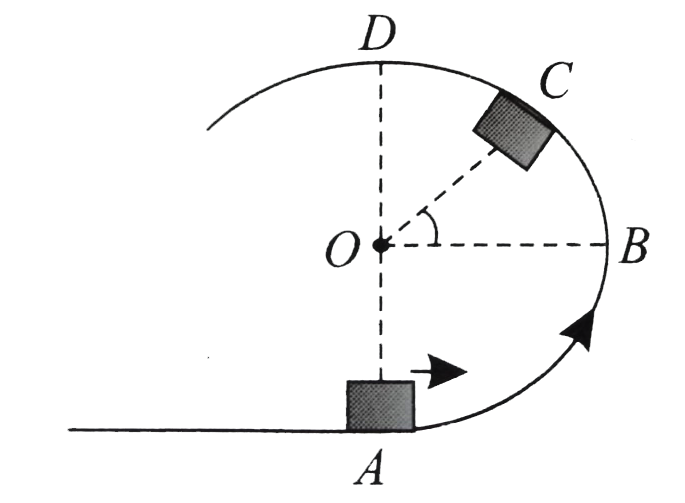
A small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
Q. Find where the maximum contact force occurs betwee the block and the track .
View SolutionFigure shows a smooth track, a part of which is a circle of radus R. As block of mass m is pushed against a sprng of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radus of the track is horizontal.
View SolutionA small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
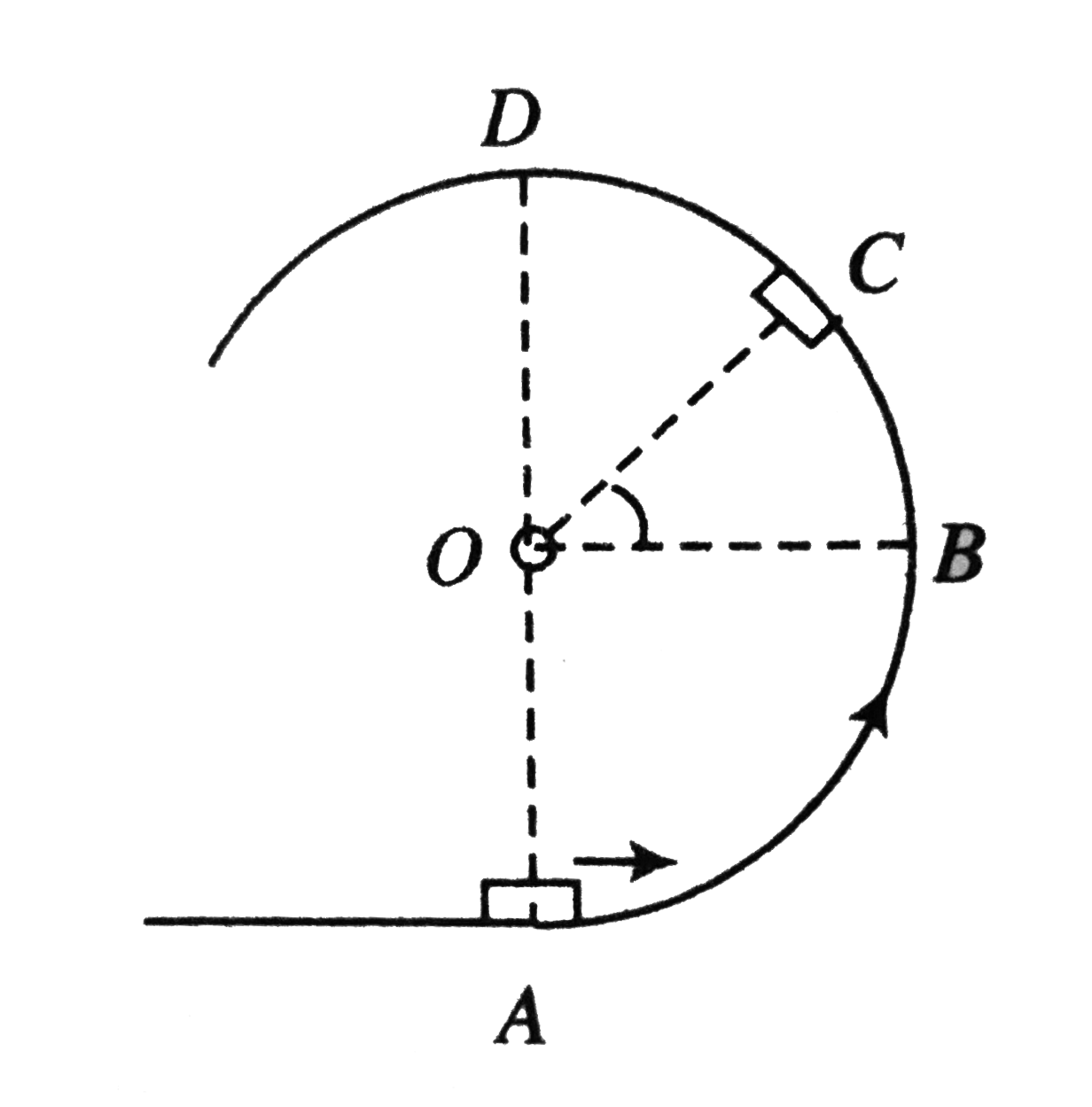
Find where the maximum contact force occurs between the block and the track.
View Solution
A small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
Q. Find where the maximum contact force occurs betwee the block and the track .
View Solution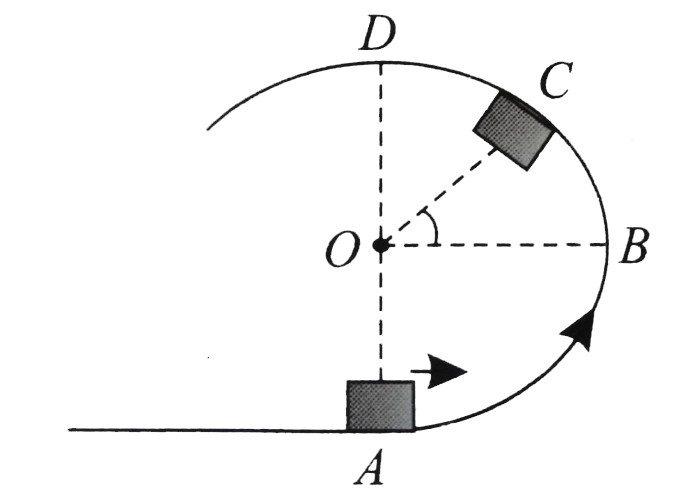
A small block of mass m is pushed on a smooth track from position A with a velocity 2√5 times the minimum velocity required to reach point D. The block will leave the contact with track at the point where normal force between them becomes zero.
Q. At what angle θ with horizontal does the block gets separated from the track?
View Solution
