A particle which is constant to move along the , is subjected to a force in the same direction which varies with the distance of the particle from the origin as . Hero and are positive constant . For , the fanctional from of the patential every U(x) of the particle is

The correct Answer is:D
To find the functional form of the potential energy U(x) of the particle subjected to the force F(x)=−Kx+ax3, we will follow these steps:
Step 1: Understand the relationship between force and potential energy
The relationship between force and potential energy is given by:
F(x)=−dUdx
This means that the force acting on the particle is equal to the negative derivative of the potential energy with respect to position.
Step 2: Write down the expression for force
Given the force:
F(x)=−Kx+ax3
Step 3: Set up the equation for potential energy
From the relationship between force and potential energy, we have:
−dUdx=−Kx+ax3
This can be rearranged to:
dUdx=Kx−ax3
Step 4: Integrate to find potential energy
To find U(x), we need to integrate the expression for dUdx:
U(x)=∫(Kx−ax3)dx
Step 5: Perform the integration
Calculating the integral:
U(x)=∫Kxdx−∫ax3dx
U(x)=K2x2−a4x4+C
where C is the constant of integration.
Step 6: Determine the constant of integration
To find the constant C, we can set the potential energy to zero at the origin (i.e., U(0)=0):
U(0)=K2(0)2−a4(0)4+C=0
This implies C=0.
Step 7: Write the final expression for potential energy
Thus, the functional form of the potential energy U(x) is:
U(x)=K2x2−a4x4
The relationship between force and potential energy is given by:
F(x)=−dUdx
This means that the force acting on the particle is equal to the negative derivative of the potential energy with respect to position.
Given the force:
F(x)=−Kx+ax3
From the relationship between force and potential energy, we have:
−dUdx=−Kx+ax3
This can be rearranged to:
dUdx=Kx−ax3
To find U(x), we need to integrate the expression for dUdx:
U(x)=∫(Kx−ax3)dx
Calculating the integral:
U(x)=∫Kxdx−∫ax3dx
U(x)=K2x2−a4x4+C
where C is the constant of integration.
To find the constant C, we can set the potential energy to zero at the origin (i.e., U(0)=0):
U(0)=K2(0)2−a4(0)4+C=0
This implies C=0.
Thus, the functional form of the potential energy U(x) is:
U(x)=K2x2−a4x4
Topper's Solved these Questions
Similar Questions
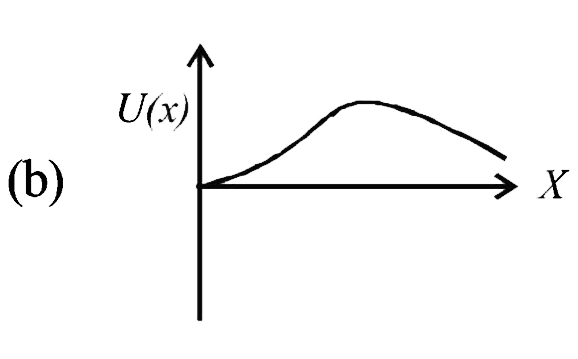
A particle, which is constrained to move along x-axis, is subjected to a force in the some direction which varies with thedistance x of the particle from the origin an F(x)=−kx+ax3. Here, k and a are positive constants. For x(≥0, the functional form of the potential energy (u) U of the U (x) the porticle is.
(a) , (b)
, (b) 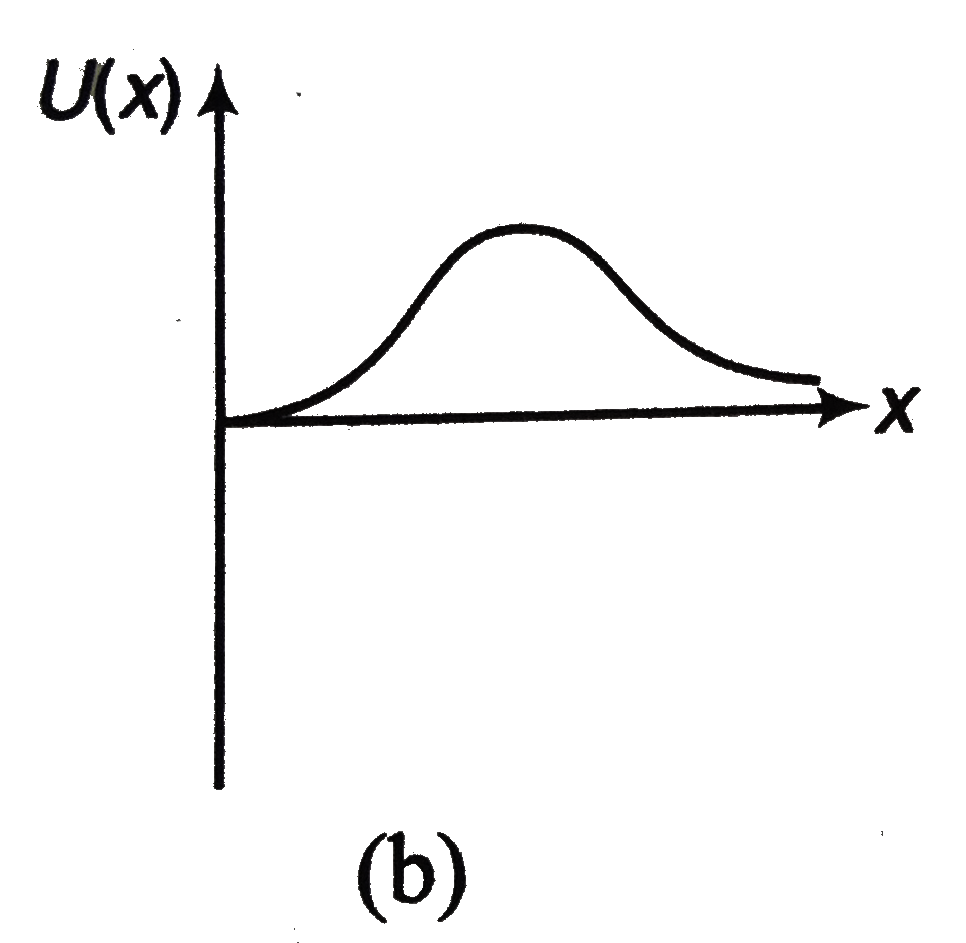 , (c)
, (c) 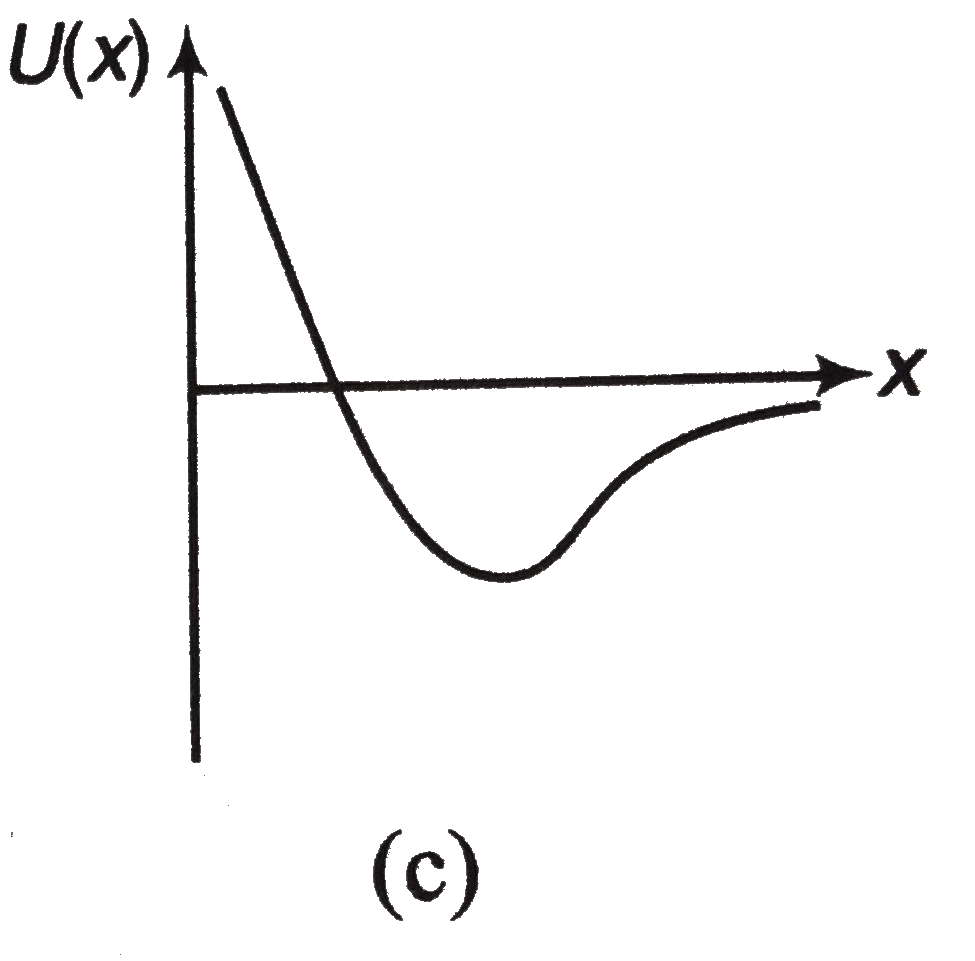 , (d)
, (d) 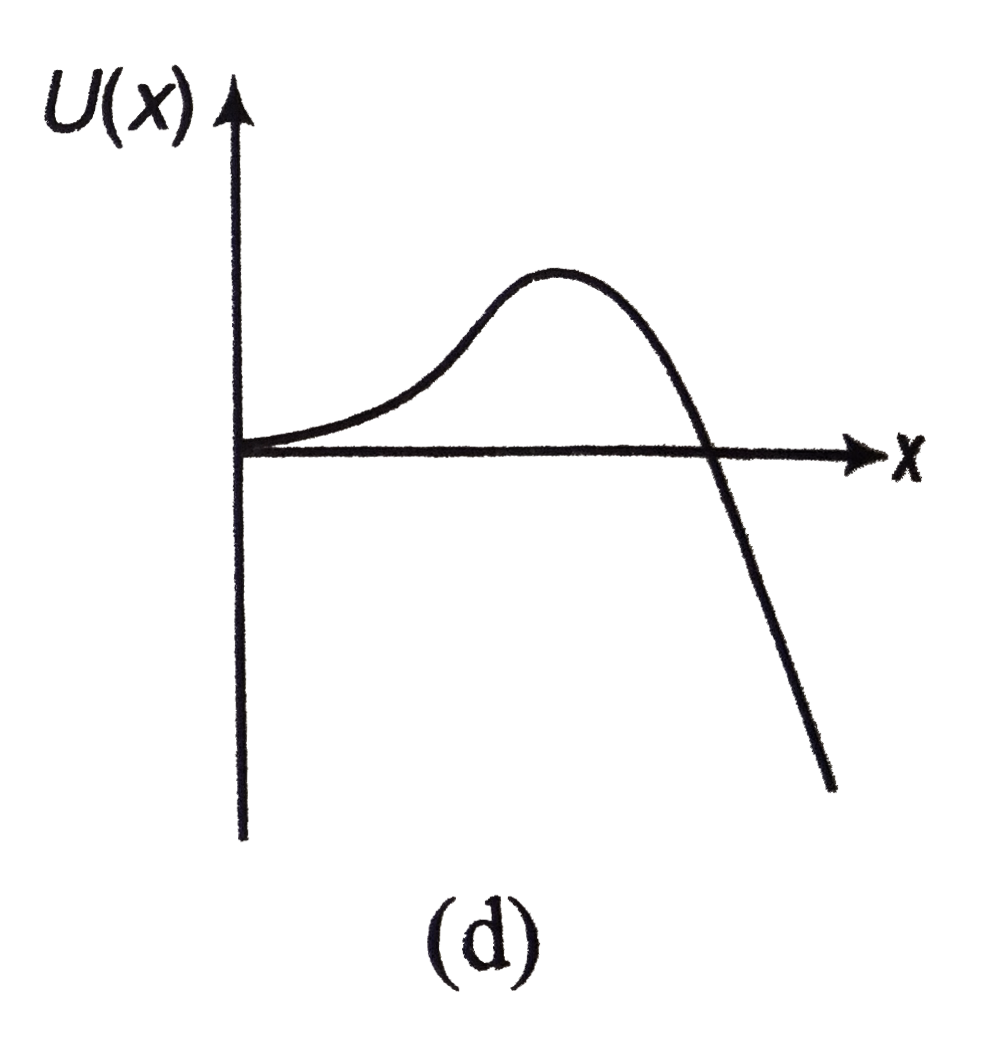 .
.
View SolutionThe kinetic energy of a particle moving along x-axis varies with the distance x of the particle from origin as K=A+x3Bx1/4+C .Write the dimensional formula for A2B
View Solution
Knowledge Check
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
A B
B C
C D
D
A particle, which is constrained to move along the x-axis, is subjected to a force from the origin as F(x)=−kx+ax3. Here k and a are origin as F(x)=−kx+ax3. Here k and a are positive constants. For x=0, the functional form of the potential energy U(x) of particle is.
A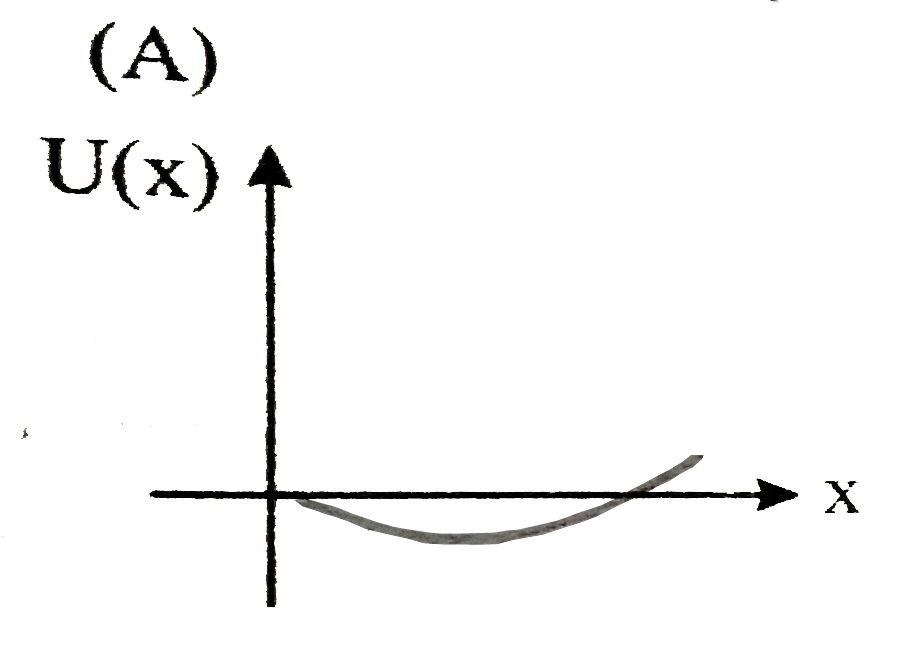 B
B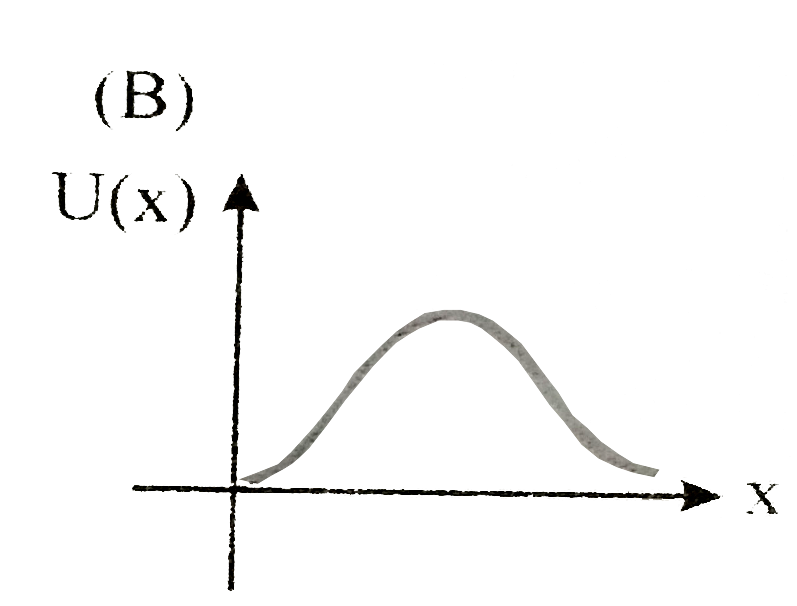 C
C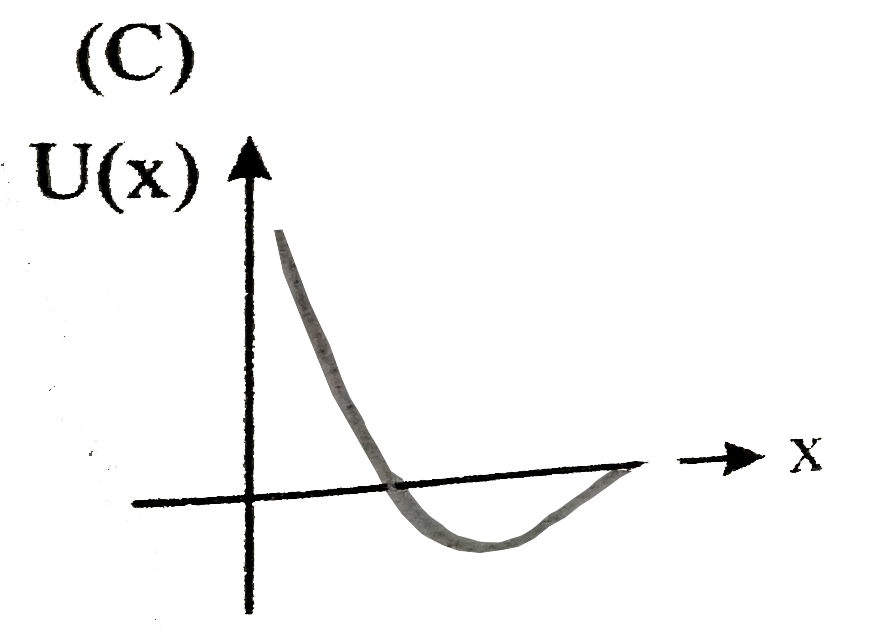 D
D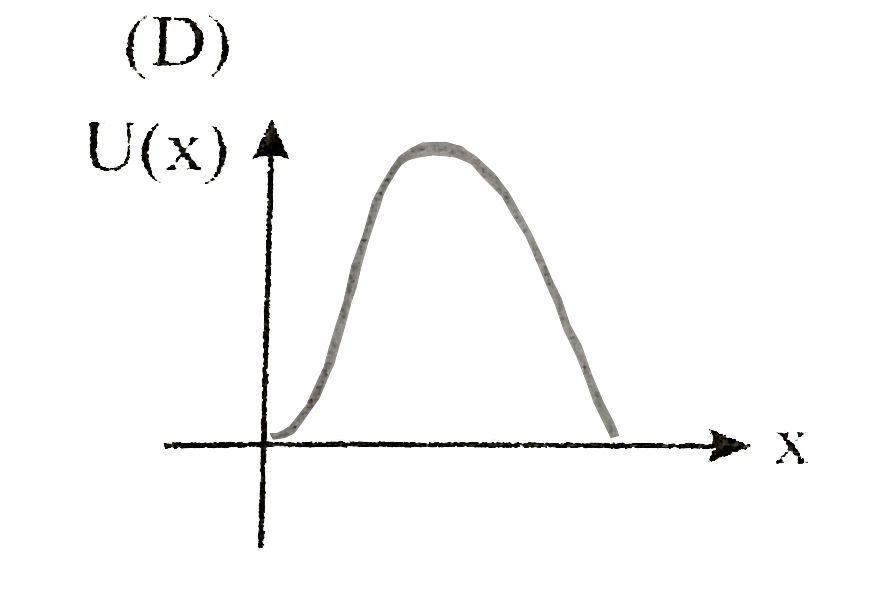
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
A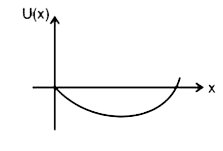 B
B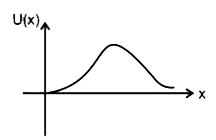 C
C D
D
A particle moving along the x- axis is subjected to a force given by F=F0(ex/a−1) where F0 and are constants Determine an expression for the work done by this force as the particle moves from the origin to the point x=r
View SolutionA particle constrained to move along the x-axis in a
potential V=kx2 is subjected to an external time dependent
force →f(t) here k is a constant, x the distance from the origin,
and t the time. At some time T, when the particle
has zero velocity at x = 0, the external force is removed.
Choose the incorrect options –
(1) Particle executes SHM
(2) Particle moves along +x direction
(3) Particle moves along – x direction
(4) Particle remains at rest
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionA particle is projected with velocity V0along axis x . The deceleration on the particle is proportional to the square of the distance from the origin i.e., a=ωx2.distance at which the particle stops is
View SolutionA particle free to move along x-axis is acted upon by a force F=−ax+bx2whrteaandbarepositiveconstants.For ximplies0, the correct variation of potential energy function U(x) is best represented by.
View Solution
