Initial angular velocity of a circualr disc of mass M is ω1. The tow sphere of mass ma re attached gently to diametrically opposite points ont eh edge of the disc. What is the final angular velocity on the disc?
(M+mM)ω1
(M+mM)ω1
(MM+4m)ω1
(MM+2m)ω1
The correct Answer is:C
(c ) When two small sphere of mass m are attached gently,
the external torque, about the axis of rotatation, is zero
and therefore the angular momentum about the axis fo
rotation is constant.
∴I1ω1=I2ω2⇒ω2=11I2ω1
Here I_1 = (1)/(2)MR^2 and I_2 = (1)/(2)MR^2 + 2mR^2<br>:. omega_2 = ((1)/(2)MR^2)/((1)/(2)MR^2 + 2mR^2 xx omega_1 = (M)/(M+4m) omega_1
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ROTATIONAL MOTIONEXERCISE - MCQs with one correct answer
1 Videos
- MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MOTIONEXERCISE - JEE Main And Advanced
63 Videos
- SIMPLE HARMONIC MOTIONBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - JEE Main And Advanced
69 Videos
Similar Questions
Angular velocity of a ring is ω. If we put two masses each of mass m at the diametrically opposite points then the resultant angular velocity (m=mass of ring)
View SolutionAngular velocity of a ring is ω. If we put two masses each of mass m at the diametrically opposite points then the resultant angular velocity (m=mass of ring)
View Solution
Knowledge Check
Initial angular velocity of a circular disc of mass M is ω1. Then two small spheres of mass m are attached gently to two diametrically opposite points on the edge of the disc. What is the final angular velocity of the disc -
A(M+mM)ω1B(M+mm)ω1C(MM+4m)ω1D(MM+2m)ω1A circular disc of mass M and radius R is rotating with angular velocity ω . If two small spheres each of mass m are gently attached to two diametrically opposite points on the edge of the disc, then the new angular velocity of the disc will be
A(M+4mM)ωB(MM+4m)ωC(M+mM)ωD(MM+2m)ωA thin circular ring of mass m and radius R is rotating about its axis perpendicular to the plane of the ring with a constant angular velocity ω. Two point particleseach of mass M are attached gently to the opposite end of a diameter of the ring. The ring now rotates, with an angular velocityω2. Then the ratiomM is
A1B2C12D√2
A horizontal disc of radius R and mas 20 M is pivoted to rotate freely about a vertical axis through its centre. A small insect A of mass M and another small insect B of mass mM4 are initially at diametrically opposite points on the periphery of the disc. The whole system is imparted an angular speed ω0 Insect A walks along the diameter with constant velocity v relative to the disc unit it reaches B which remains at rest on the disc. A then eats B and returns to its starting point along the original path with same speed v relative to the disc.
(a) Find the angular speed of the disc when A reaches the centre after eating B.
(b) Plot approximately, the variation of angular speed of the disc with time for the entire journey of the insect A.
View SolutionA disc of mass M and radius R is rotating about its axis with initial angular velocity of ω0 as shown. Now two small masses of m each one kept on the circumference diametrically opposite to eachother. Find new angular velocity
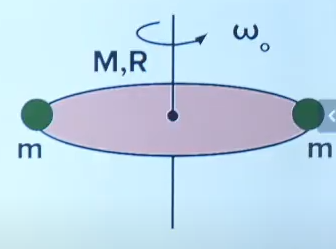
View SolutionThe angular velocity of circular disc of radius 2cm is 20 rad s−1. Calculate the linear velocity of the disc.
View SolutionA uniform dis of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Find
(A) the angular velocity of the disc.
(B) the impulse on the particle due to disc
( C) the impulse on the disc due to hinge.
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim.
The angular velocity of the disc after the particle sticks to it is
View Solution
