The magnitude of electric field →E in the annular region of a charged cylindrical capacitor.
(a) is same throughout
(b) is higher near the outer cylinder than near the inner cylinder
(c) varies as 1/r, where r is the distance from axis
(d) varies as 1/r2 where r is the distance from the axis.
The correct Answer is:C
Let λ be the charge per unit length. Let us consider a Gaussian surface (dotted cylinder).
Applying Gauss's law
ϕ=∮→E.→ds=λlε0
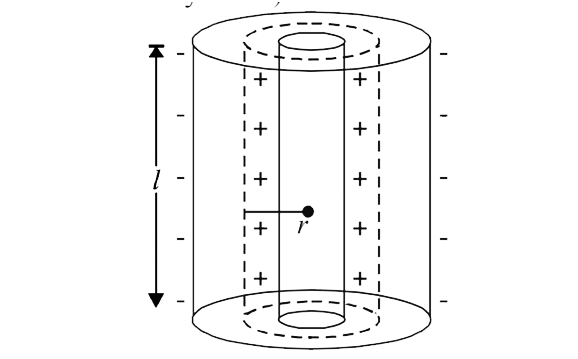
For the flat portions of Gaussian surface, the angle between electric field and surface is 90∘. Hence flux through flat portions is zero.
The angle between →E and →ds is 0∘ (for curved surface)
⇒E∫ds=λlε0⇒E×2πrl=λlε0
⇒E=λ2πε0r⇒E∝1r
Topper's Solved these Questions
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Subjective Problems
2 Videos
- ELECTROSTATICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROSTATICSEXERCISE - Comprehension Based Questions
2 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTEXERCISE - JEE Main And Advanced
107 Videos
- MODERN PHYSICSBOOK - SUNIL BATRA (41 YEARS IITJEE PHYSICS)CHAPTER - MODERN PHYSICSEXERCISE - MCQ (One Correct Answer
1 Videos
Similar Questions
The magnitude of electric field intensity and electric potential due to a point charge at a point is 72 N/C and 36V, respectively. Calculate magnitude of the charge and distance of the point from point charge.
View SolutionDerive an expression for the electric field intensity at a point outside an infinitely long charged cylindrical conductor.
View Solution
Knowledge Check
The magnitude of electric field →E in the annular region of a charged cylindrical capacitor.
Ais same throughoutBis higher near the outer cylinder than near the inner cylinderCvaries as 1/r where r is distance from the axisDvaries as 1/r2 where r is distance from the axisHow does the electric field (E) between the plates of a charged cylindrical capacitor vary with the distance r from the axis of the cylinder ?
AE∝1r2BE∝1rCE∝r2DE∝rA uniform electric field →E exists between the plates of a charged condenser. A charged particle enters the space between the plates and perpendiculars to →E. The path of the particle between the plates is a
AStraight lineBhyperbolaCparabolaDcircle
Show that the force on each plate of a parallel plate capacitor has a magnitude equal to 12QE, where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor 12.
View SolutionShow that the force on each plate of a parallel plate capacitor has a magnitude equal to (½)QE, where Q is the charge on the capacitor, and E is the magnitude of electric field between the plates. Explain the origin of the factor ½.
View SolutionThe magnitude of electric field intensity due to a point charge is 10 N/C at a distance 1 m from it. Calculate the magnitude of charge.
View SolutionA cube of side 20 cm is kept in a region as shown in the figure. An electric field →E exists in the region such that the potential at a point is given by V=10x+5, where V is in volt and x is in m.
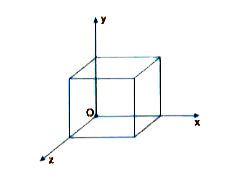
Find the
(i) electric field →E, and
(ii) total electric flux through the cube.
View SolutionThe potential field of an electric field →E=(yˆi+yˆi) is
View Solution
