A metal rod moves at a constant velocity in a direction perpendicular to its length. A constant, uniform magnetic field exists in space in a direction perpendicular to the rod as well as its velocity. Select the correct statements(s) from the following
The entire rod is at the same electric potential.
There is an electric field in the rod.
The electric potential is highest at the centre of the rod and decreases towards its ends.
The electric potential is lowest at the centre of the rod, and increases towards its ends.
The correct Answer is:B
To analyze the situation described in the question, we need to apply the principles of electromagnetic induction, specifically Faraday's law and the Lorentz force.
1. Understanding the Setup:
- We have a metal rod (let's call it rod AB) that is moving with a constant velocity v in a direction perpendicular to its length.
- There is a uniform magnetic field B that is also perpendicular to both the rod and its direction of motion.
2. Applying the Lorentz Force:
- As the rod moves through the magnetic field, the charges (electrons) within the rod experience a force due to the magnetic field. This force is given by the Lorentz force equation:
F=q(→v×→B)
- Here, q is the charge of the electrons, →v is the velocity of the rod, and →B is the magnetic field.
3. Direction of the Force:
- The direction of the force can be determined using the right-hand rule. If you point your thumb in the direction of the velocity of the rod and your fingers in the direction of the magnetic field, your palm will face the direction of the force acting on positive charges (which is opposite to the direction of the force acting on negative charges like electrons).
- This results in a separation of charges within the rod, creating an electric field.
4. Induced Electromotive Force (EMF):
- The separation of charges leads to a potential difference (voltage) across the ends of the rod. This induced voltage (or EMF) can be calculated using the formula:
EMF=B⋅L⋅v
- Where L is the length of the rod.
5. Conclusion:
- The moving rod in a magnetic field induces an electromotive force due to the motion of the charges within it. The rod will have a higher potential at one end and a lower potential at the other end, leading to a potential difference across the rod.
- We have a metal rod (let's call it rod AB) that is moving with a constant velocity v in a direction perpendicular to its length.
- There is a uniform magnetic field B that is also perpendicular to both the rod and its direction of motion.
- As the rod moves through the magnetic field, the charges (electrons) within the rod experience a force due to the magnetic field. This force is given by the Lorentz force equation:
F=q(→v×→B)
- Here, q is the charge of the electrons, →v is the velocity of the rod, and →B is the magnetic field.
- The direction of the force can be determined using the right-hand rule. If you point your thumb in the direction of the velocity of the rod and your fingers in the direction of the magnetic field, your palm will face the direction of the force acting on positive charges (which is opposite to the direction of the force acting on negative charges like electrons).
- This results in a separation of charges within the rod, creating an electric field.
- The separation of charges leads to a potential difference (voltage) across the ends of the rod. This induced voltage (or EMF) can be calculated using the formula:
EMF=B⋅L⋅v
- Where L is the length of the rod.
- The moving rod in a magnetic field induces an electromotive force due to the motion of the charges within it. The rod will have a higher potential at one end and a lower potential at the other end, leading to a potential difference across the rod.
Topper's Solved these Questions
Similar Questions
A metallic metre sitck moves with a velocity of 2 ms ^(-1) in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf indcued between the ends of the stick.
View SolutionA conducting rod of unit length moves with a velocity of 5m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.4T. Find the emf induced between the ends of the stick.
View Solution
Knowledge Check
A n electrically charged particle enters into a uniform magnetic induction field in a direction perpendicular to the field with a velocity v then it travels
Aina straight line without accelerationBwith force in the direction of the fieldCin a circular path with a radius directly proportional toDin a circular path with a radius directly proportional to its velocityA proton and an electron are projected into a region of uniform magnetic field in a direction perpendicular to the field. If they have the same initial velocities then
AThey move in circular paths of same radiiBThey experience equal forceCThe trajectory of the electron is more curvedDTheir velocity remain equal to each other through out the motionA conducting loop rotates with constant angular velocity about its fixed diameter in a uniform magnetic field, whose direction is perpendicular to that fixed diameter.
A(a) The emf will be maximum at the moment when flux is zeroB(b) The emf will be 0 at the moment when flux ismaximumC( c) The emf will be maximum at the moment when plane of the loop is parallel to the magnetic fieldD(d) The phase difference between the flux and the emf π/2
A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular ot the diameter joining free ends, (b) the velocity is parallel to this diameter.
View SolutionA conducting rod of length L is carrying a constant current I. There exists a magnetic field B perpendicular to the rod. Due to the magnetic force the rod moved through a distance x in a direction perpendicular to the field (B) as well as its own length. The rod acquires a kinetic energy. A student says that a magnetic force ILB acted on the rod and it performed a work W=ILBx on the rod. But we know that magnetic force is always perpendicu- lar to the velocity of the charge and it cannot perform work on a moving charge. Which agency has actually spent energy to impart kinetic energy to the rod?
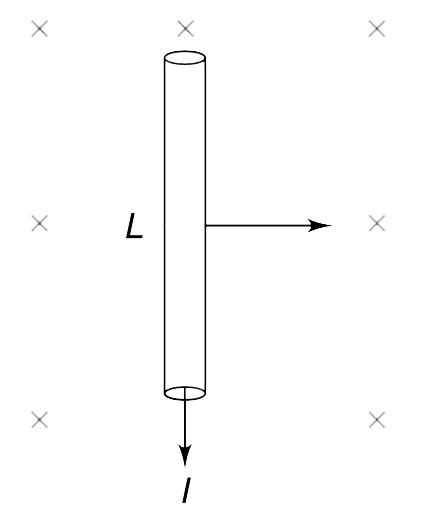
View SolutionA conducitng rod AB of length l=1m moving at a velcity v=4m/s making an angle 30∘ with its length. A uniform magnetic field B=2T exists in a direction perpendicular to the plane of motion. Then :

View SolutionA neutral metal bare moves at a constant velocity v to the right through a region of uniform magnetic field directed out the page, as shown. Therefore,

View SolutionAssertion When a charged particle moves perpendicular to a uniform magnetic field then its momentum remains constant.
Reason Magnetic force acts perpendicular to the velocity of the particle.
View Solution
