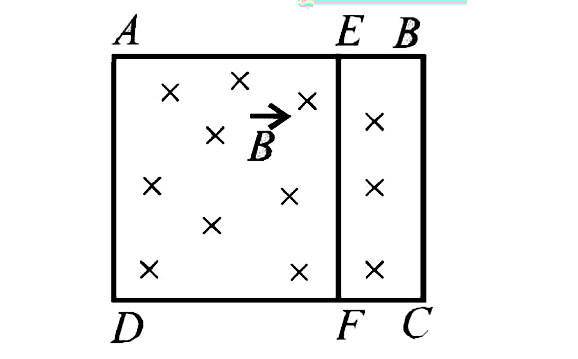
A rectangular frame ABCD, made of a uniform metal wire, has a straight connection between E and F made of the samae wire, as shown in fig. AEFD is a square of side 1m, and EB=FC=0.5m. The entire circuit is placed in steadily increasing, uniform magnetic field directed into the plane of the paper and normal to it. The rate of change of the magnetic field is 1T/s. The resistance per unit length of the wire is 1ω/m. Find the magnitude and directions of the currents in the segments AE, BE and EF.
The correct Answer is:A, B
The equivalent circuit is drawn in the adjecent figure

As the magnetic field increase in the downward direction, an induced emf will be produced in the AEFD as well as in the circuit EBCF such that the current flowing in the loop creates magnetic lines of force in the upward direction (to the plane of paper)
Thus, the current should flow in the anticlockwise direction in both the loops.
Induced emf in loop AEFD
e=−dϕdt=−ddtBA=−AdBdt=−1×1=−vo<
Induced emf in loop EBCF
e=−dϕdt=−ddtBA'=−A'dBdt=−0.5×1=−0.5vo<<br>Letthecurrentflow∈g∈thebranchEADFbe(i_1)andthecurrentflow∈g∈thebranchFCBEbe(i_2).Apply∈gjunctionlawatF,we≥tcurrent∈branchFE→be(i_(1)-i_(2))<br>Apply∈gKirchhoff'slaw∈l∞pEADFE<br>-1xx(I_1)-1xx(I_1)+1-1xx(I_1)-1(i_(1)-i_(2))=0
⇒4(i1)−(i2)=1...(i)
Appying Kirchhoff's law in loop EBCDFE
+0.5(i1)−0.5+1(i2)−1(i1−i2)=0
−(i1)+3(i2)=0.5 ...(ii) Solving (i) and (ii)
11(i1)=3.5
⇒(i1)=3.5/11=722A
Also 11(i2)=3
⇒(i2)=3/11A=622A
∴Current∈segmentAE=(i1)=722A
current∈segmentBE=(i2)=622A
Current in segment EF=(i1−i2)=122A.
Topper's Solved these Questions
Similar Questions
A closed loop with the geometry shown in Fig. 3.9 is placed in a uniform magnetic field direction into the plane of the paper. If the magnetic field decreases with time, determine the direction of the induced emf in this loop.

View SolutionThe figure-4.240 shows ·a square wire mesh made of conducting wires. Here, each small square has side a. The structure is kept in uniform magnetic field B perpendicular to the plane of paper:
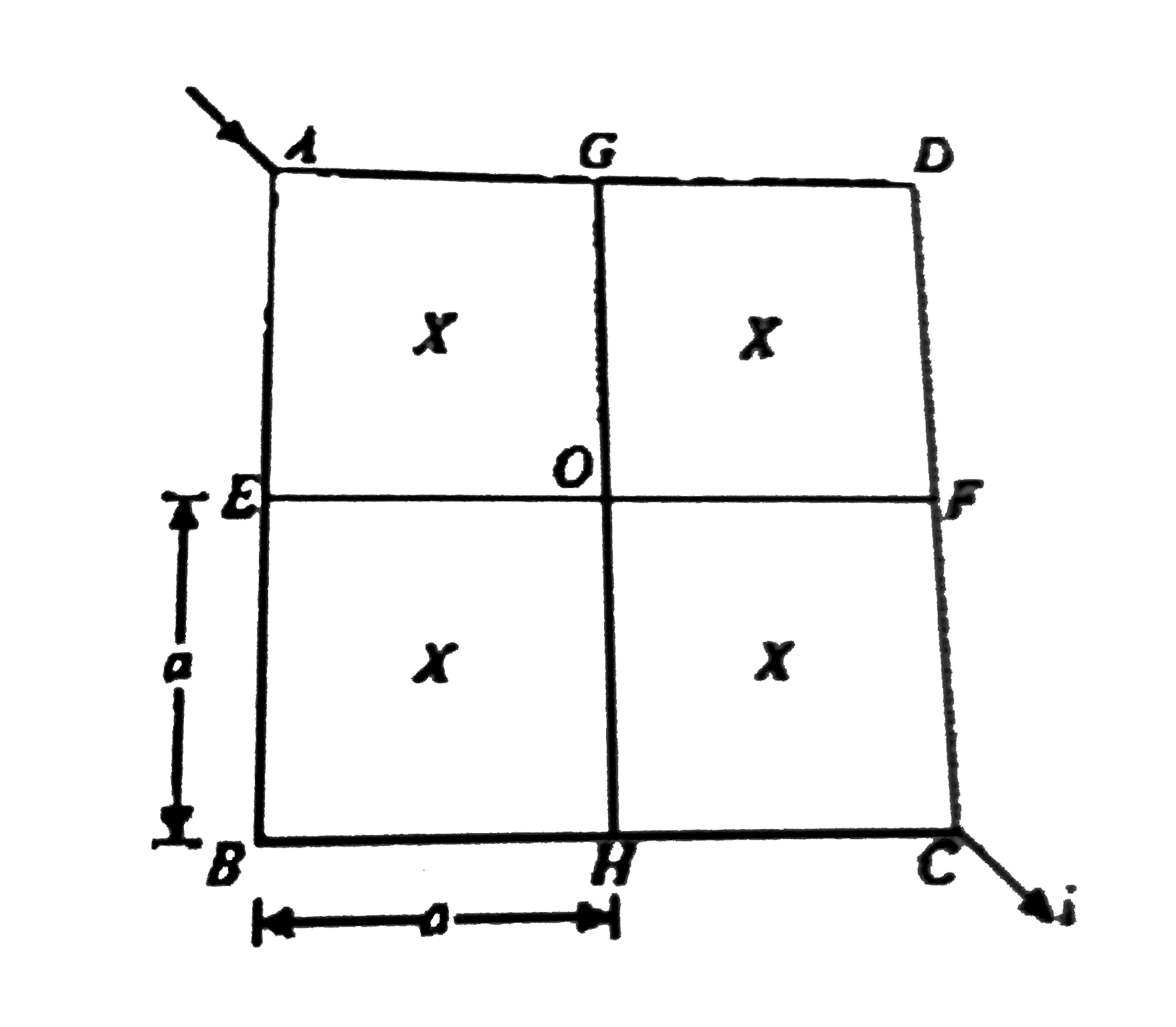
View Solution
Knowledge Check
The counductor AD moves to the right in a uniform magnetic field directed into the plane of the paper.
 A(a) The free electron in AD will move toward AB(b) D will acquire a positive potential with respect to AC(c ) A current will flow from A→D in AD in closed loopD(d) The current in AD flows from lower to higher potential
A(a) The free electron in AD will move toward AB(b) D will acquire a positive potential with respect to AC(c ) A current will flow from A→D in AD in closed loopD(d) The current in AD flows from lower to higher potentialA magnetic field is directed normally downwards through a metallic frame as shown in the figure . On increasing the magnetic field __
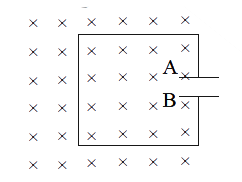 Aplate B will be positively chrgedBplate A will be positively chargedCnone of the plates will be positively chargedDall of the above
Aplate B will be positively chrgedBplate A will be positively chargedCnone of the plates will be positively chargedDall of the aboveIn the circuit shown in Fig. A conducting wire HE is moved with a constant speed v towards left. The complete circuit is placed in a uniform magnetic field →B perpendicular to the plane of circuit inwards. The current in HKDE is
 AclockwiseBanticlockwiseCdirection will change with timeDzero
AclockwiseBanticlockwiseCdirection will change with timeDzero
A coil of metal wire is kept stationary in a non-uniform magnetic field. An e.m.f. Is induced in the coil.
View SolutionIn Fig., a semicircular wire is placed in a uniform field →B directed towards right. Find the resultant magnetic force and torque on it.

View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in newton in both the cases a and b. The radius of the loop is 1.0 m

View SolutionA long conducting wire AH is moved over a conducting triangular wire CDE with a constant velocity v in a uniform magnetic field →B directed into the plane of the paper. Resistance per unit length of each wire is ρ. Then
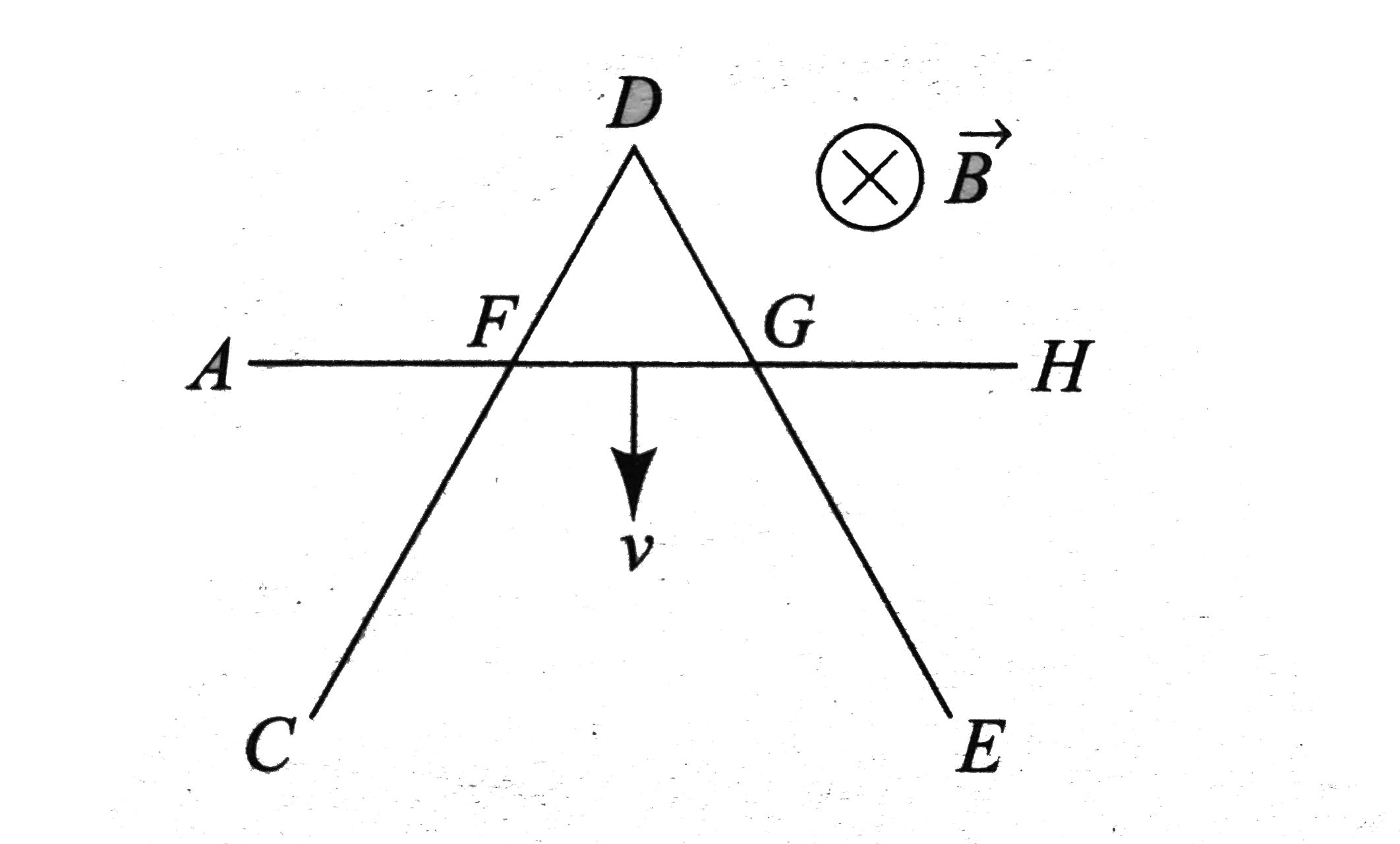
View SolutionA wire is bent in the form of an equilateral triangle of side 1m and carries a current of 2A.. It is placed in a magnetic field of induction 2.0 T directed into the plane of paper. The direction and magnitude of magnetic force acting on each side of the triangle will be
View Solution
