Two long parallel horizontal rails a, a distance d aprt and each having a risistance λ per unit length are joing at one end by a resistance R. A perfectly conduction rod MN of mass m is free to slide along the rails without friction (see figure). There is a uniform magnetic field of induction B normal to the plane of the paper and directed into the paper. A variable force F is applied to the rod MN such that, as the rod moves a constant current flows through R.
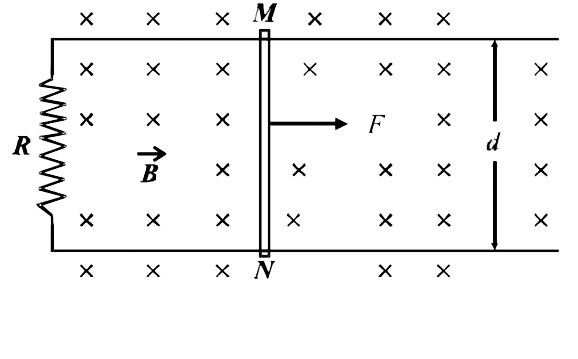
(i) Find the velocity of the rod and the applied force F as function of the distance x of the rod from R.
(ii) What fraction of the work done per second by F is converted into heat?
The correct Answer is:A, B, C, D
(i) A variable force F is applied to the rod MN such that as the rod moves in the uniform magnetic field a constant current flows through R. Consider the loop MPQN. Lenght of rails in loop =2x.
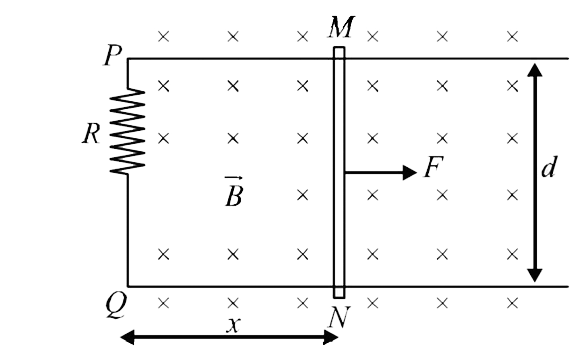
Resistance of rails in loop =2x(λ)
Total resistance of loop=R+2(λ)x
Induced emf =Bvd
Induced current (I)=BvdR+2λx
so for constant I,
v=R+2λxBdI
Furthermore, as due to induced current I the wire will experience force FM=BId opposite to its motion, the equation of motion of the wire will be
F−(FM)=mai.e.,F=(FM)+ma
But as here (Fm)=Bld and from equation (i)
a=dvdt=2λlBddxdt=2λivBd0=2λI2Bd2(R+2λx)
so, F=Bld+2λmI2(Bd)2(R+2λx)
(ii) As the work done by force F per sec.
dWdt=P=Fv=[bld+2λmI2(Bd)2(R+2λx)][R+2λxBd.I]
i,e.,P=[(I62)(R+2λx)=2λmI3b3d3(R+2λx)2]
and heat produced per second, i.e., joule heat
H=(I2)(R2λx)
so, f=HP=[1+2λmI(R+2λx)B3d3]−1.
Topper's Solved these Questions
Similar Questions
Two long parallel horizonal rails , a distance d apart and each having a resistance λ per unit length are jointed at one end by a resitance R. A perfectly conducting rod MN of mass m is free to slide along the rails . A variable force F is applied to the rod MN , such that ,as the rd moves, a constant current i flows through R.
(a) Find the velocity v and the force F as function of the function of the distance x of the rod from R.

(b) What fraction η of the work done by F per second in converted into heat ?View SolutionShows a rod of length l and resistance r moving on two rails shorted by a resistance R. A uniform magnetic field B is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A conducting rod AB moves parallel to x-axis in a uniform magnetic field pointing perpendicular and into the plane of paper. The end A of the rod
 Agets positively chargedBgets negatively chargedCremains neutralDgets positively charged first and then negatively charged
Agets positively chargedBgets negatively chargedCremains neutralDgets positively charged first and then negatively charged - Question 2 - Select One
A vertical ring of radius r and resistance on R falls vertically. It is in contact with two vertical rails which are joined at the top. The rails are without friction and resistance. There is a horizontal uniform, magnetic field of magnitude B perpendicular to the plane of the ring and the rails. When the speed of the ring is v , the current in the section PQ is
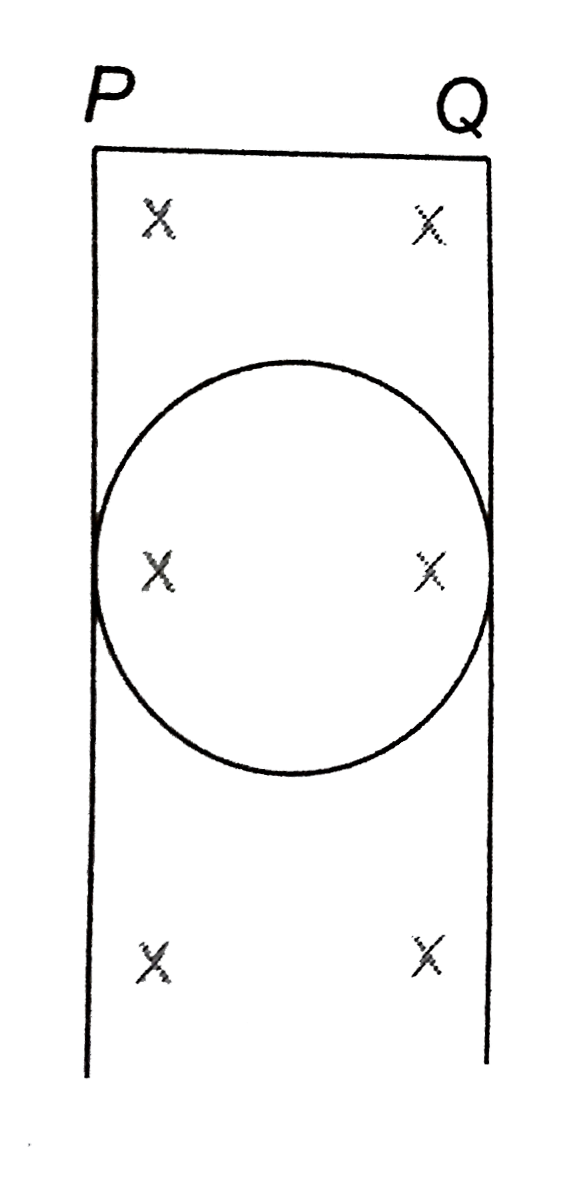 AzeroB2BvRC4BrvRD8BrvR
AzeroB2BvRC4BrvRD8BrvR - Question 3 - Select One
Two long rails are hporizontal and parallel to each. On one end, the rails are connected by a resistance R and on the other end a cpacitor of capacitance C is connected as shown in the figure . A connecter of mass m and length l can slide on the rails without friction. Uniform magnetic field B, perpendicular to he plane of hte gigure exists in space. A constant horizontal force F starts acting on hte connector. What is the acceleration of connector when its veleocity is 34 of its terminal velocity?
 A3F4(m+CB2I2)BF(m+CB2I2)CF4(m+CB2I2)D4F3(m+CB2I2)
A3F4(m+CB2I2)BF(m+CB2I2)CF4(m+CB2I2)D4F3(m+CB2I2)
A long conducting wire AH is moved over a conducting triangular wire CDE with a constant velocity v in a uniform magnetic field →B directed into the plane of the paper. Resistance per unit length of each wire is ρ. Then
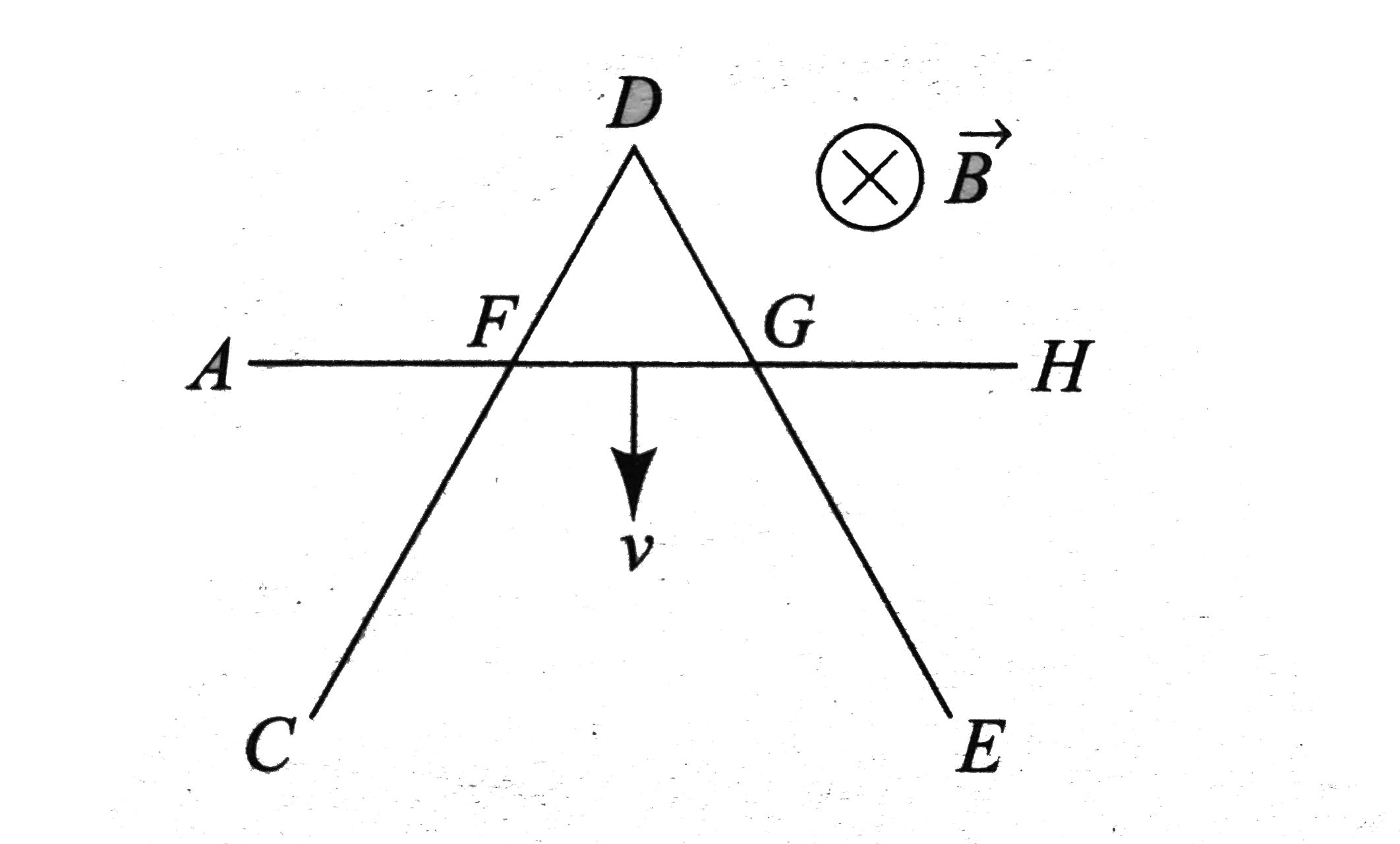 View Solution
View SolutionA copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle θ to the horizontal. At the bottom, the rails are joined by a resistance R.

There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod isView SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of
 View Solution
View SolutionAB and CD are fixed conducting smooth rails placed in a vertical palne and joined by a constant current source at its upper end. PQ is a conducting rod which is free to slide on the rails. A horizontal uniform magnetic field exists in space as shwn in figure. If the rod PQ is released from rest then,
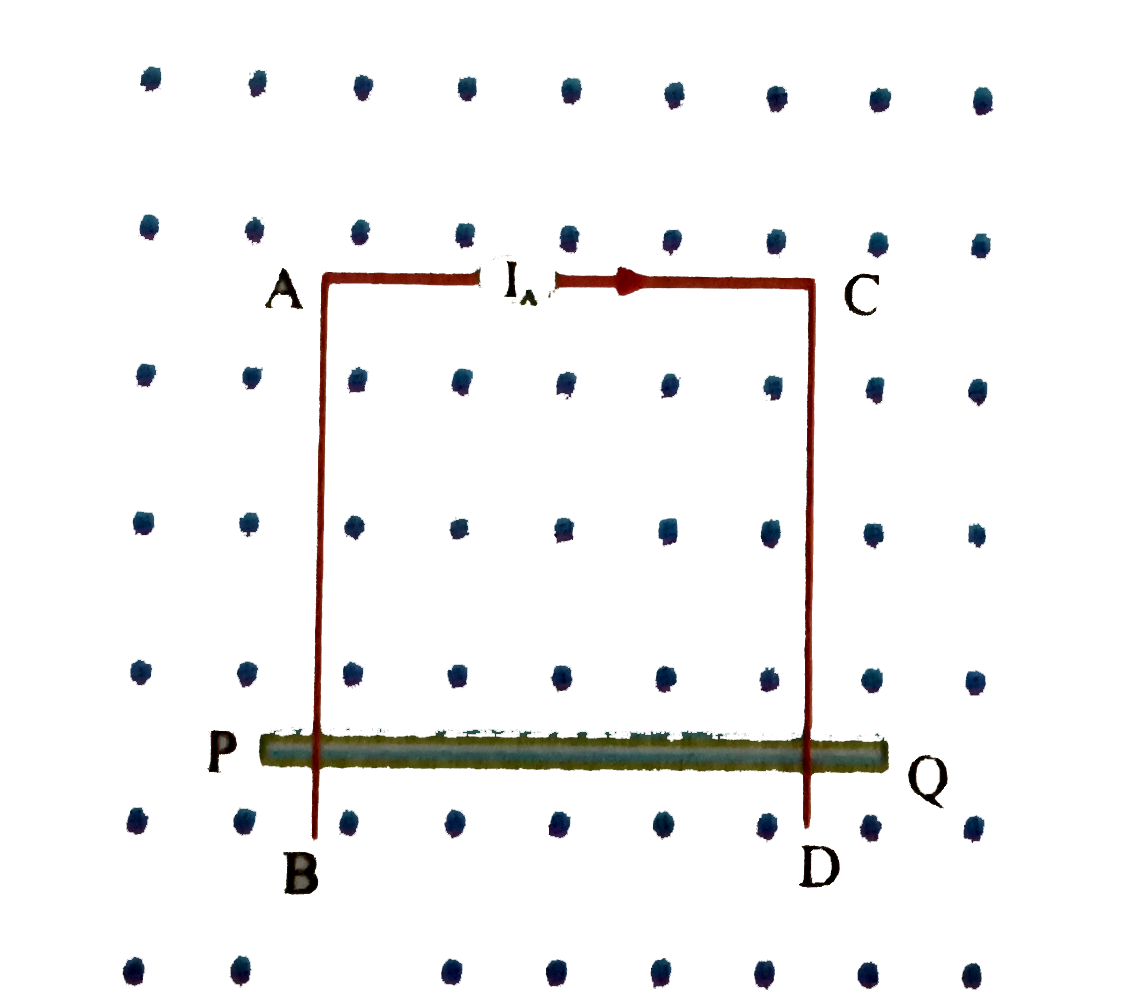 View Solution
View SolutionA conducting rod is free to slide along a pair of conducting rails, in a region where a uniform and constant (in time) magnetic field is directed into the plane of the paper, as the drawing illustrates. Initially the rod is at rest. There is no frictio between the rails and the rod. What happens to the rod after the switch is closed? If any induced emf devlops, be sure to account for its effect.
 View Solution
View Solution

