AB is the common tangent to the circles C1 and C2. C1 and C2 are touching externally at C.AD and DC are two chords of the circle C1 and BE and CE are two chords of the circle C2. Find the measure of ∠ADC+∠BEC
Step by step video solution for AB is the common tangent to the circles C_1 and C_2. C_1 and C_2 are touching externally at C.AD and DC are two chords of the circle C_1 and BE and CE are two chords of the circle C_2. Find the measure of /_ADC+/_BEC by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
दिखाए गये चित्रानुसार दोनो वृतों के केंद्रों C1 तथा C2 के मध्य दुरी 35 है अर्थात C1C2=35 तथा C1 व C2 केंद्रों वाले वृतों की त्रिज्याएँ क्रमशः 12 व 9 है । यदि वृतों की उभयनिष्ठ आंतरिक स्पर्श रेखा तथा C1C2 का प्रतिच्छेद बिंदु P है, तो l(C1P) का मान होगा
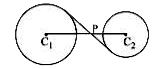
(i) 18 (ii) 20 (iii) 12 (iv) 15
View SolutionIn the figure given, two circles with centres Ct and C2 are 35 units apart, i.e. C1C2=35. The radii of the circles with centres C1 and C2 are 12 and 9 respectively. If P is the intersection of C1C2 and a common internal tangent to the circles, then l(C1P) equals
View SolutionThe internal common tangents to two circles with centre C1 and C2 intersect the line joining C1 andC2 at P and the two direct common tangents intersects the line joining C1 and C2 at Q. The length C1P, C1C2 and C1 Q are in
View SolutionC1andC2 are fixed circles of radii r1andr2 touches each other externally. Circle 'C' touches both Circles C1andC2 extemelly. If r1r2=32 then the eccentricity of the locus of centre of circles C is
View SolutionLet C1and C2 be two circles with C2 lying inside C1 circle C lying inside C1 touches C1 internally andexternally. Identify the locus of the centre of C
View SolutionTransverse common tangents are drawn from O to the two circles C_1,C_2 with 4, 2 respectively. Then the ratio of the areas of triangles formed by the tangents drawn from O to the circles C_1 and C_2 and chord of contacts of O w.r.t the circles C_1 and C_2 respectively is
View SolutionIn the figure given, two circles with centres Ct and C2 are 35 units apart, i.e. C1C2=35. The radii of the circles with centres C1 and C2 are 12 and 9 respectively. If P is the intersection of C1C2 and a common internal tangent to the circles, then l(C1P) equals
View SolutionLet C_1 and C_2 be two circles with C_2 lying inside C_1 A circle C lying inside C_1 touches C_1 internally and C_2 externally. Identify the locus of the centre of C
View Solution
