The mode of the following frequency distribution is 46 and the total frequency is 150. Find the missing frequencies x and y.
Here, we are given total frequency is 150.
6+8+17+x+42+30+y+8=150
⇒x+y+111=150
⇒x+y=39
It means, both x and y does not exceed 42.
So, our modal class wil be 40−50.
Now, Mode can be given by formula,
Mode=l+f1−f02f1−f0−f2∗h
Here, l= Lower limit of modal class =40
f1= Frequency of Modal class =42
f2= Frequency of Pre Modal class =x
f3= Frequency of Succeeding Modal class =30
h= Class interval =10
Putting these values in Mode formula,
Mode=40+42−x84−30−x∗10=40+42−x54−x∗10
We are given, Mode=46
⇒40+42−x54−x∗10=46
⇒42−x54−x∗10=6
⇒42−x54−x=610
⇒42−x54−x=35
⇒210−5x=162−3x
⇒2x=48
⇒x=24
⇒y=39−24⇒y=15
Similar Questions
Find the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. No. of accident (x) 0 1 2 3 4 5 Total Frequency (f): 46 ? ? 25 10 5 200
View SolutionFind the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. No. of accident (x), 0, 1 , 2 , 3, 4, 5 , Total Frequency is 200 and no. of days (f): 46 , ? , ? , 25 , 10 , 5
View SolutionFind the missing frequencies in the following frequency distribution if it is known that the mean of the distribution is 1.46. No of accident (x) 0 1 2 3 4 5 Total Frequency (f): 46 ? ? 25 10 5 200
View Solutionनिम्न बारम्बारता-बंटन में छूटी हुई बारम्बारताओ को ज्ञात कीजिए। यदि यह ज्ञात हो कि बंटन का माध्य 1.46 है।
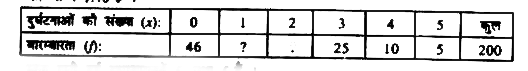
View SolutionFind the mode of the following frequency distribution.

View SolutionFind the mode of the following frequency distribution

View SolutionFind the mode of the following frequency distribution.

View SolutionAn incomplete frequency distribution is given below
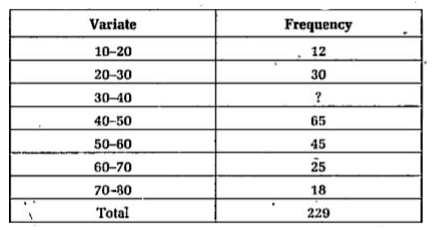
Median value is 46, the missing frequency is
View Solution