Consider the equation [|x−1|−|x+2|=p.Let ρ be the value of ρ for which the equationOne solution. Also ρ2, is the value of ρ for which the equation has infinite solution.Let a be the sum of all the integral values of ρ for which this equation has solution ρ , is equal to
Step by step video & image solution for Consider the equation [|x-1|-|x+2|=p.Let rho be the value of rho for which the equationOne solution. Also rho_2, is the value of rho for which the equation has infinite solution.Let a be the sum of all the integral values of rho for which this equation has solution rho , is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
An ideal gas equation can be written as P=ρRTM0 where ρ and M are resp.
Amass density, mass of gasBnumber density, molar massCmass density, molar massDnumber density, mass of gasA thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to
A√3−12−√3B√3+12+√3C√3−1√3+1D√3+1√3−1The densities at points A and B are ρ0 and 3ρ02. Find the value of x on P-axis.
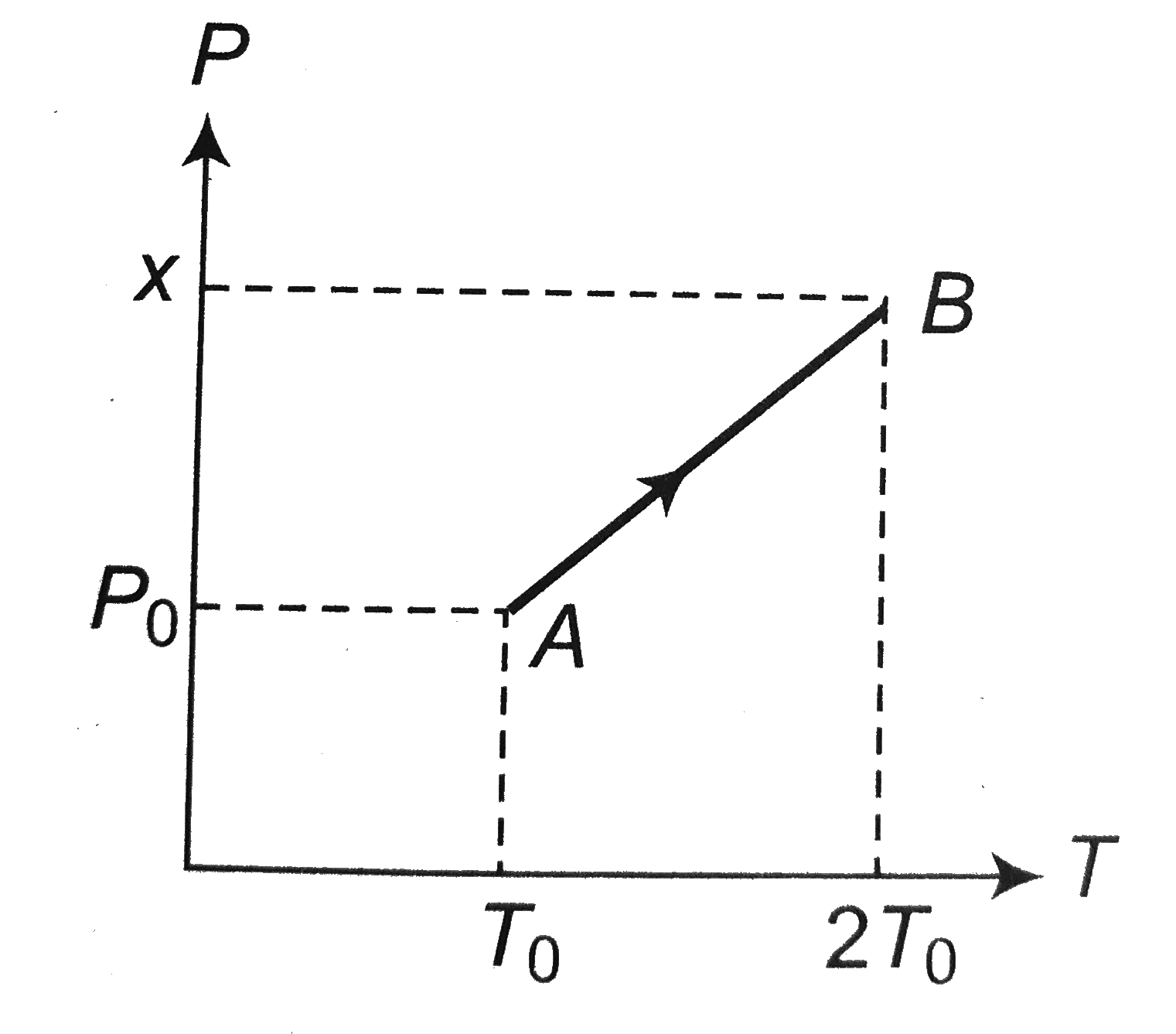A2P0B32P0C3P0D4P0
An ideal gas equation can be written as P=ρRTM0 where ρ and M are resp.
View SolutionA thin uniform circular tube is kept in a vertical plane. Equal volume of two immiscible liquids whose densites are ρ1 and ρ2 fill half of the tube as shown. In equilibrium the radius passing through the interface makes an angle of 30∘ with vertical. The ratio of densities (ρ1/ρ2) is equal to
View SolutionA planet has a core of density ρ1 and the density of the outer shell is ρ2. R and 3R are the radii of the core and the planet respectively. Also, it is given that gravitational acceleration at the surface of the planet is equal to that at the surface of core. Hence, compute the ratio e ratio ρ1ρ2.
View SolutionThree liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ3), having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
View SolutionThree liquids of densities ρ1,ρ2 and ρ3 (with ρ1>ρ2>ρ2) having the same value of surface tension T, rise to the same height in three identical capillaries. The angles of contact θ1,θ2 and θ3 obey
View Solution