Diameter AB of a circle with centre O is produced to point P such that PO = 16.5 cm. PQR is a secant which intersects the circle at Q and R such that PQ = 12 cm and PR = 19.2 cm. The length of AB (in cm) is:
केंद्र O वाले एक वृत्त के व्यास AB को बिंदु P तक इस प्रकार बढ़ाया जाता है कि PO = 16.5 सेमी है |
PQR एक छेदक रेखा है जो वृत्त को Q तथा R पर इस प्रकार काटती है कि PQ = 12 सेमी तथा PR = 19.2 सेमी है | AB की लंबाई ( सेमी में ) कितनी है ?
15.8
14.2
15.2
14.4
To find the length of diameter AB of the circle, we can use the Power of a Point theorem, which states that for a point P outside a circle, the product of the lengths of the segments of any secant line through P is equal to the square of the length of the tangent segment from P to the circle.
1. Identify the Given Values:
- PO (the distance from point P to the center O) = 16.5 cm
- PQ (the length from P to point Q on the circle) = 12 cm
- PR (the length from P to point R on the circle) = 19.2 cm
2. Calculate the Length of QR:
- The length of QR can be calculated as:
QR=PR−PQ=19.2cm−12cm=7.2cm
3. Apply the Power of a Point Theorem:
- According to the theorem:
PO2=PQ⋅PR
- Substitute the known values:
(16.5)2=12⋅19.2
4. Calculate PO^2:
- Calculate PO2:
16.52=272.25
5. Calculate PQ \cdot PR:
- Calculate PQ⋅PR:
12⋅19.2=230.4
6. Set Up the Equation:
- Now we have:
272.25=230.4+AB2
- Rearranging gives:
AB2=272.25−230.4=41.85
7. Find the Length of AB:
- Taking the square root to find AB:
AB=√41.85≈6.46cm
8. Conclusion:
- The length of diameter AB is approximately 6.46 cm.
- PO (the distance from point P to the center O) = 16.5 cm
- PQ (the length from P to point Q on the circle) = 12 cm
- PR (the length from P to point R on the circle) = 19.2 cm
- The length of QR can be calculated as:
QR=PR−PQ=19.2cm−12cm=7.2cm
- According to the theorem:
PO2=PQ⋅PR
- Substitute the known values:
(16.5)2=12⋅19.2
- Calculate PO2:
16.52=272.25
- Calculate PQ⋅PR:
12⋅19.2=230.4
- Now we have:
272.25=230.4+AB2
- Rearranging gives:
AB2=272.25−230.4=41.85
- Taking the square root to find AB:
AB=√41.85≈6.46cm
- The length of diameter AB is approximately 6.46 cm.
Topper's Solved these Questions
Similar Questions
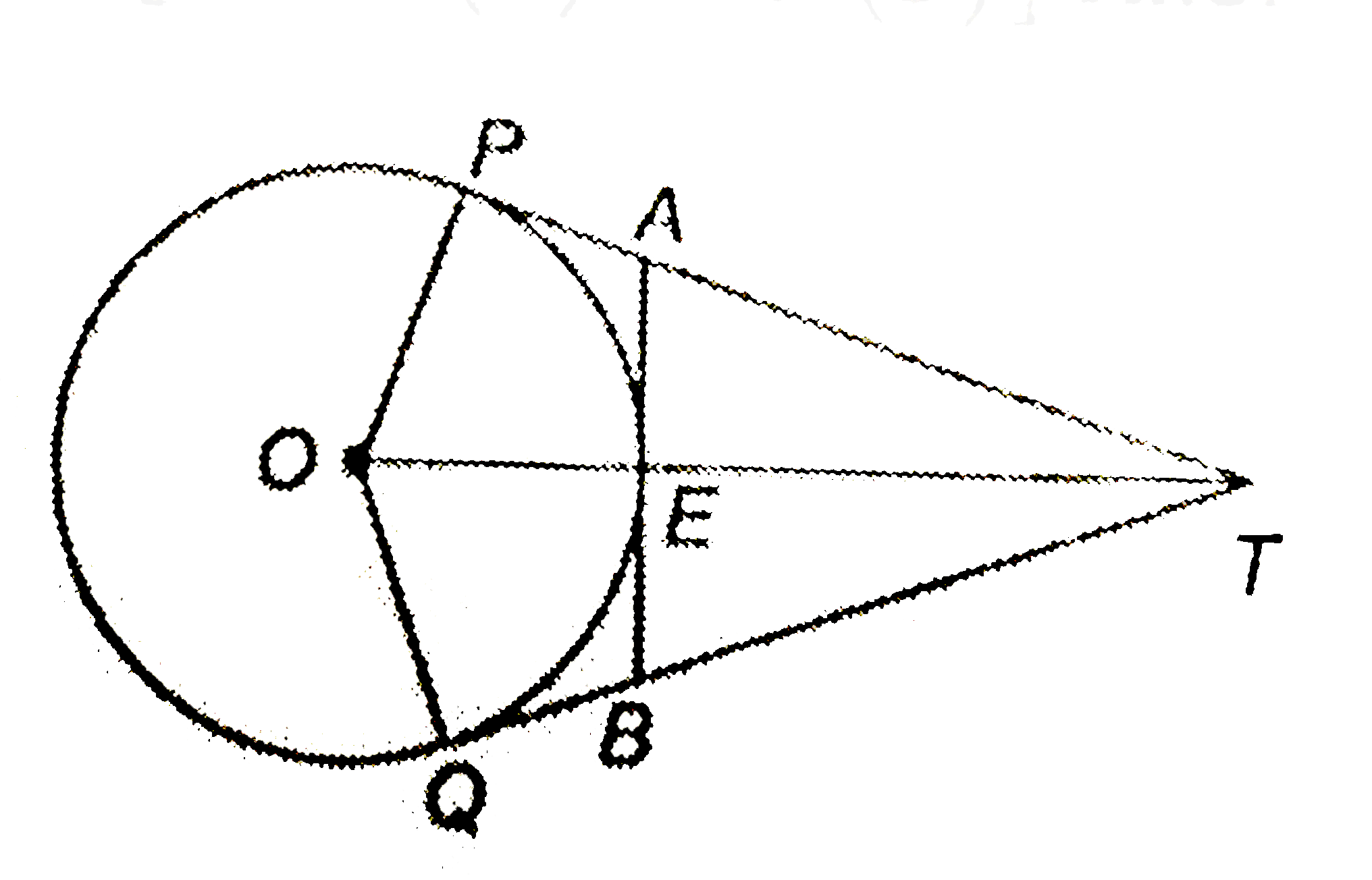
O is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E, find the length AB.
View SolutionChord AB of a circle is produced to a point P, and C is a point on the circle such that PC= 12cm, and BP = 10cm, then the length of AB (in cm ) is:
किसी वृत्त का जीवा ७8 को एक बिंदु P तक बढ़ाया जाता है, और C वृत्त पर एक बिंदु इस प्रकार है की PC=12cm, और BP = 10cm, फिर AB की लंबाई (सेमी में) है
View Solution
Knowledge Check
P is a point outside a circle with centre O, and it is 14 cm away from the centre. A secant PAB drawn from P intersects the circle at the points A and B such that PA = 10 cm and PB = 16 cm. The diameter of the Circle is:
A10 cmB13 cmC12 cmD11 cmChord AB = 10 cm of a circle with centre o produce AB such that BP = 8 cm and a tangent PC drawn from P on the circle, the length of PC is
A144 cmB18 cmC12 cmD10 cmO is the centre of a circle of radius 5cm. T is a point such that OT=13cmandOT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
A20 cmB203cmC10cmD25 cm
O is the centre of a circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find length of AB.
View SolutionP is a point out side a circle, which is 13 cm from the centre. A line drawn from point P intersects the circle at point A and B such that PA = 9 cm and AB = 7 cm. Then find the radius of the circle.
View SolutionAB is a chord of a circle with O as centre. C is a point on the circle such that OC is perpendicular to AB and OC intersects AB at P. If PC = 2 cm and AB = 6 cm then the diameter of the circle is
View SolutionType V: O is the center of the circle of radius 5cm. T is a point such that OT=13cm and OT intersects the circle at E . If AB is the tangent to the circle at E; find the length of AB.
View SolutionChords AB and CD of a circle intersect externally at P. If AB=6cm,CD=3cmandPD=5cm, then the length of PB is
View Solution