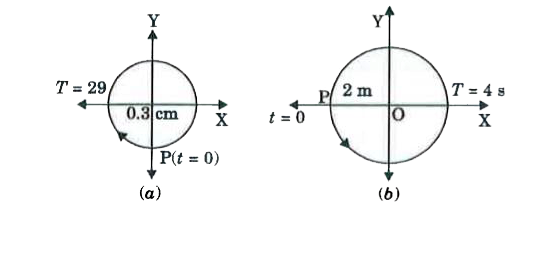
The radius of cirlcue, the period of revolution, initial position and sense of revolution are indicated in the figure.
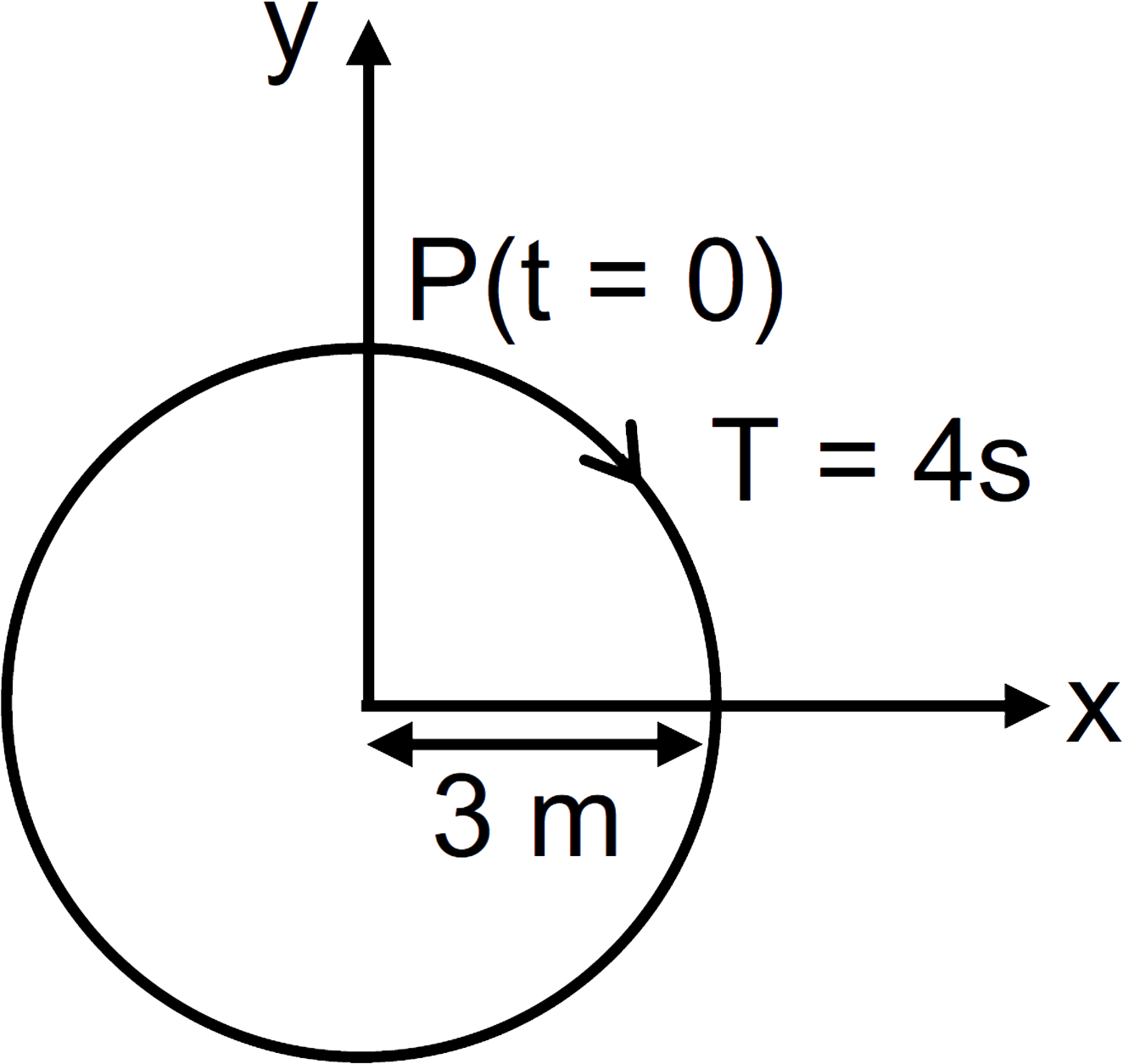
y-projection of the radius vector of rotating particle P is :
, where y in m
, where y in m
, where y in m
, where y in m
The correct Answer is:A
y co-ordinate starts from maximum
So
Topper's Solved these Questions
- NEETBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - QUESTION
95 Videos
- NEETBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - MCQ
95 Videos
- NEETBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEETEXERCISE - MCQ
95 Videos
- MOTION IN TWO AND THREE DIMENSIONBOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - MOTION IN TWO AND THREE DIMENSIONEXERCISE - All Questions
47 Videos
- NEET 2020BOOK - NEET PREVIOUS YEAR (YEARWISE + CHAPTERWISE)CHAPTER - NEET 2020EXERCISE - All Questions
45 Videos
Similar Questions
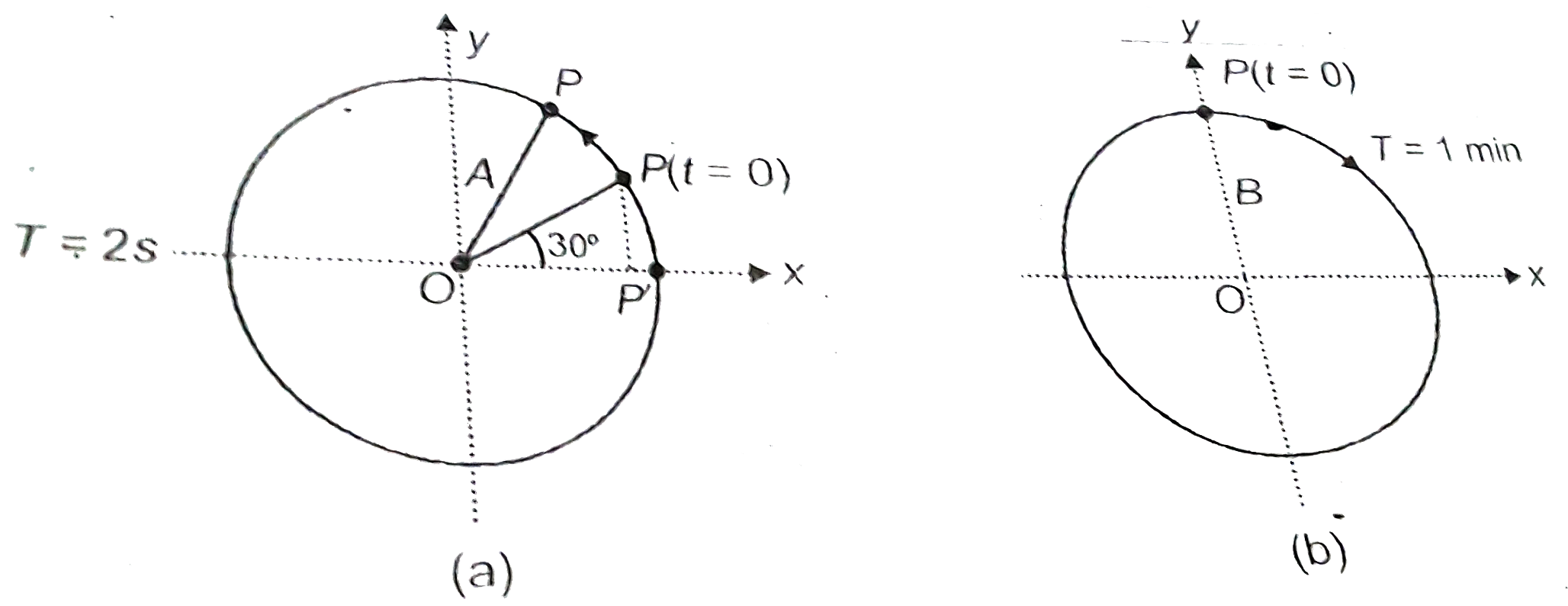
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.
View Solutiondepict two circulat mothions. The radius of the circle, the period of revolution, the initial position and sense of revolution are indicated in the figures. Obtain the simple harmonic motinosof the x-projection of the radius vector of the rotating particle P in each case.
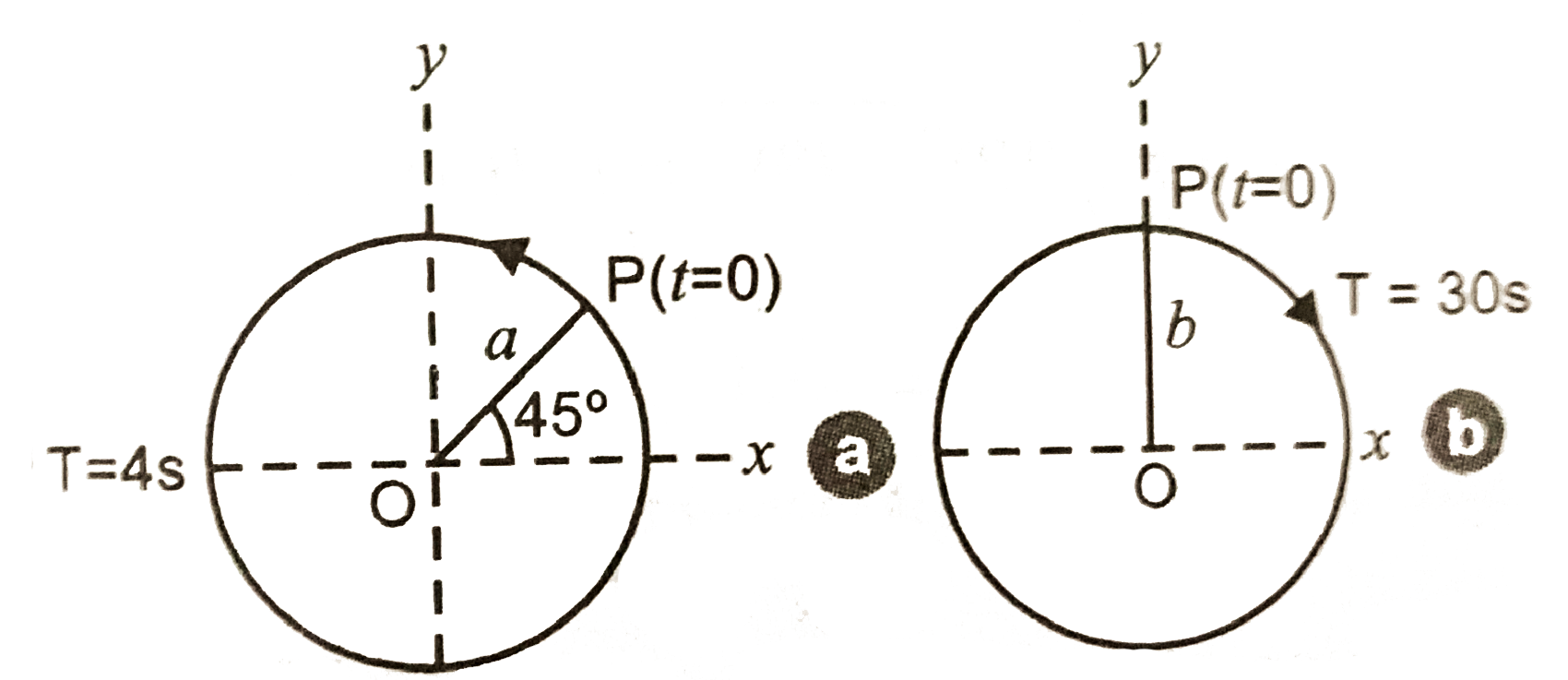
View Solution
Knowledge Check
The following figure depicts two circular motions. The radius of the circle, the period of revolutin the initial position and the sense of revolution are indicated on the figure. Obtain the simple harmoic motion of the x-projection of the radius vector of the rotating particle P in each case.
 Ax(t)=acos(2πt4+π4)Bx(t)=acos(πt4+π4)Cx(t)=asin(2πt4+π4)Dx(t)=acos(πt3+π2)
Ax(t)=acos(2πt4+π4)Bx(t)=acos(πt4+π4)Cx(t)=asin(2πt4+π4)Dx(t)=acos(πt3+π2)Figure shows the circular motion of a particle. The radius of the circle, the period, same of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector the rotating particle P is
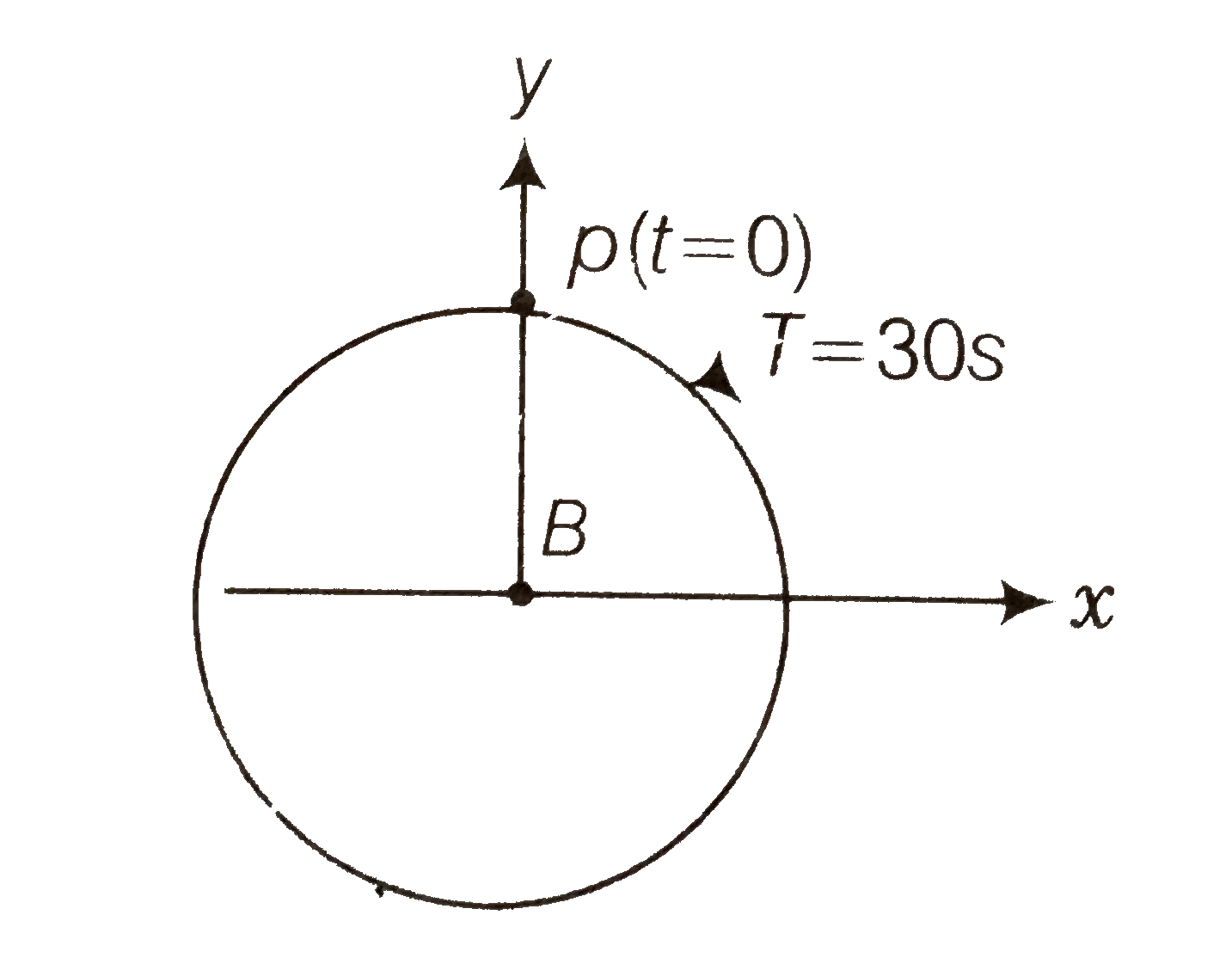 Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)
Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is
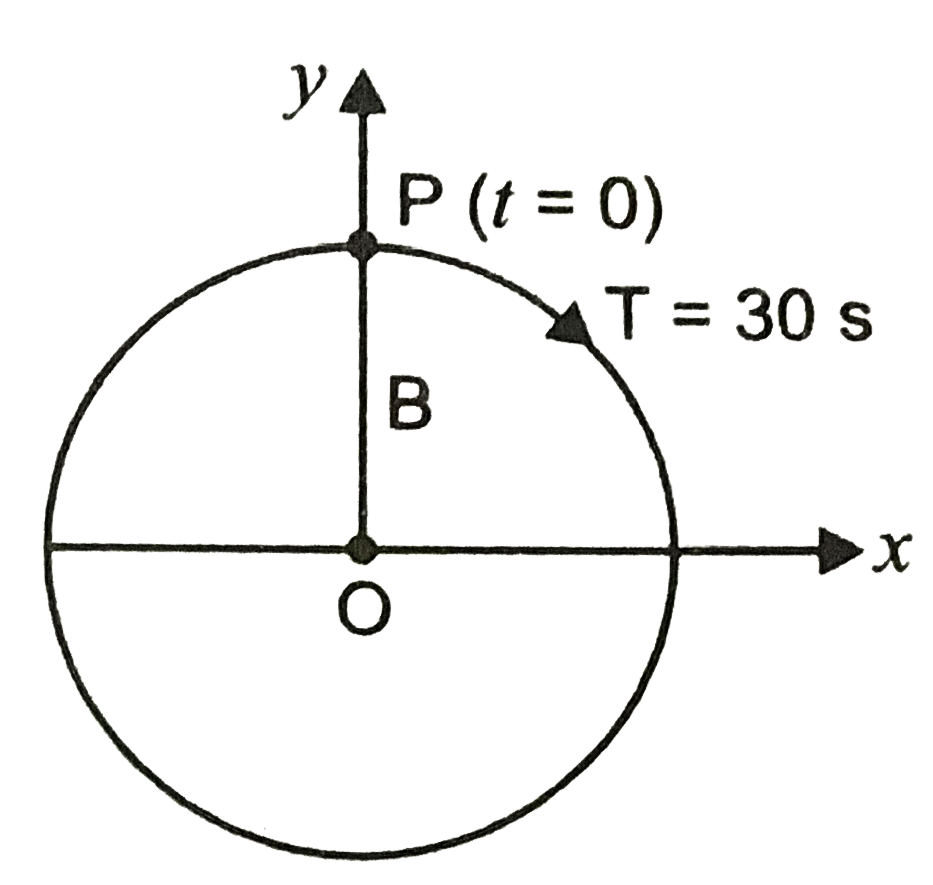 Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)
Ax(t)=Bsin(2πt30)Bx(t)=Bcos(πt15)Cx(t)=Bsin(πt15+π2)Dx(t)=Bcos(πt15+π2)
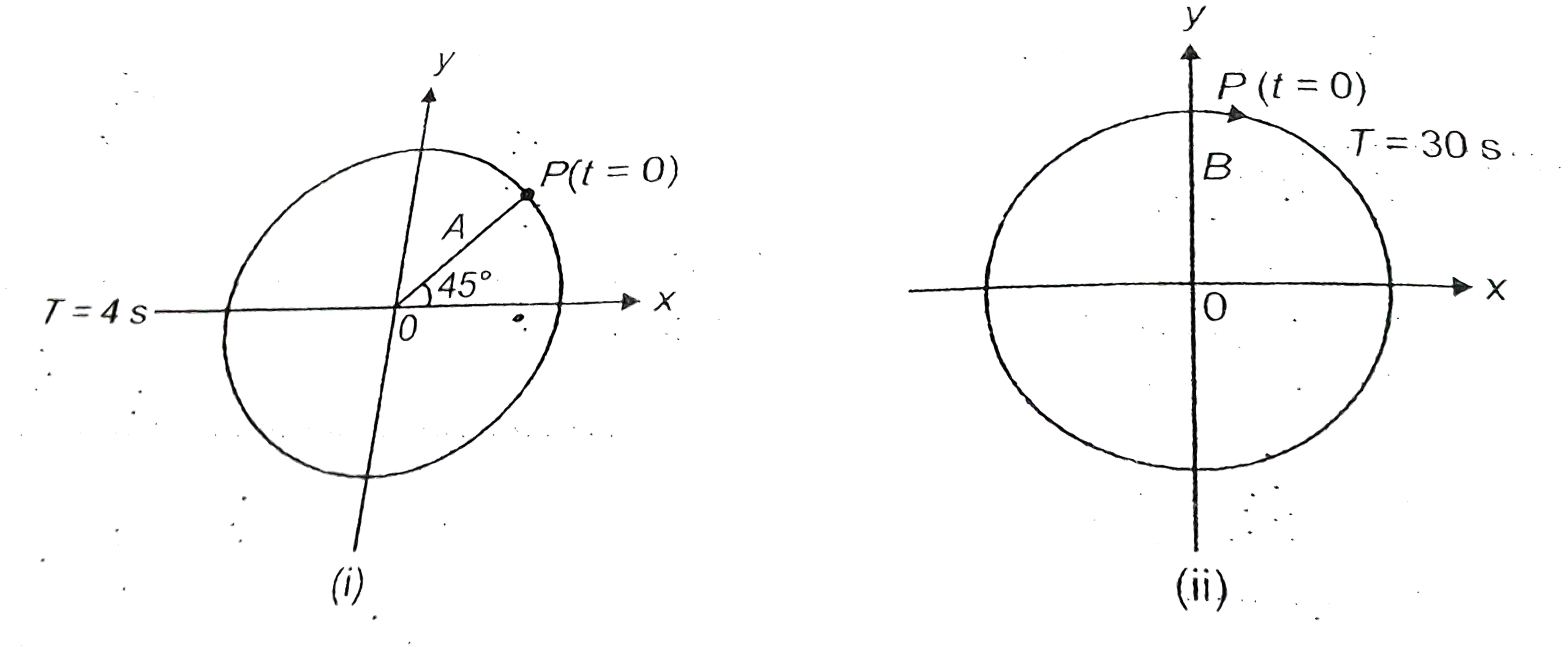
The following figure depicts two circular motions. The radius of the circle, the period of revolutin the initial position and the sense of revolution are indicated on the figure. Obtain the simple harmoic motion of the x-projection of the radius vector of the rotating particle P in each case.

View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated in the · figure. The simple harmonic motion of the X-projection of the radius vector of the rotating particle Pis
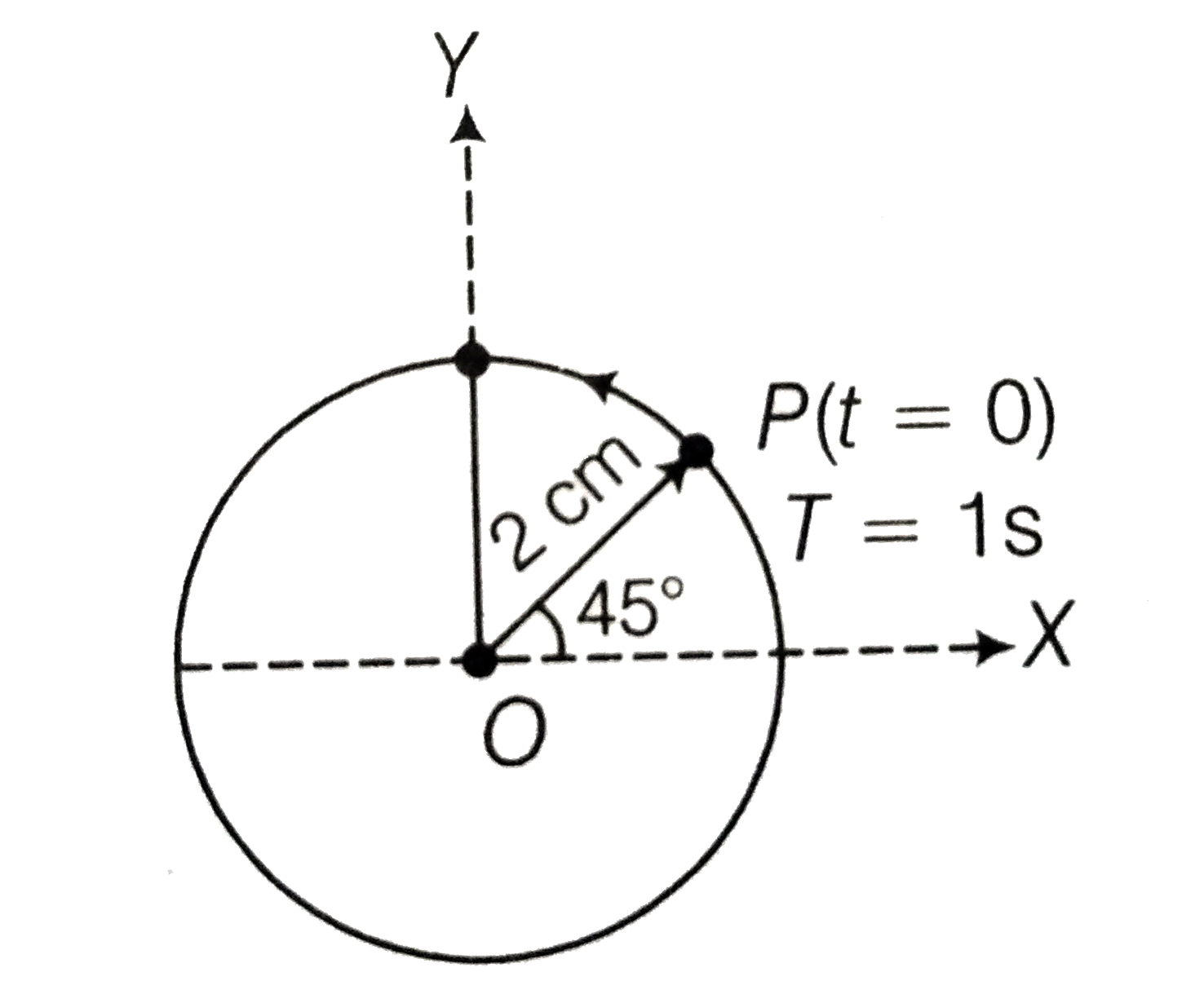
View Solution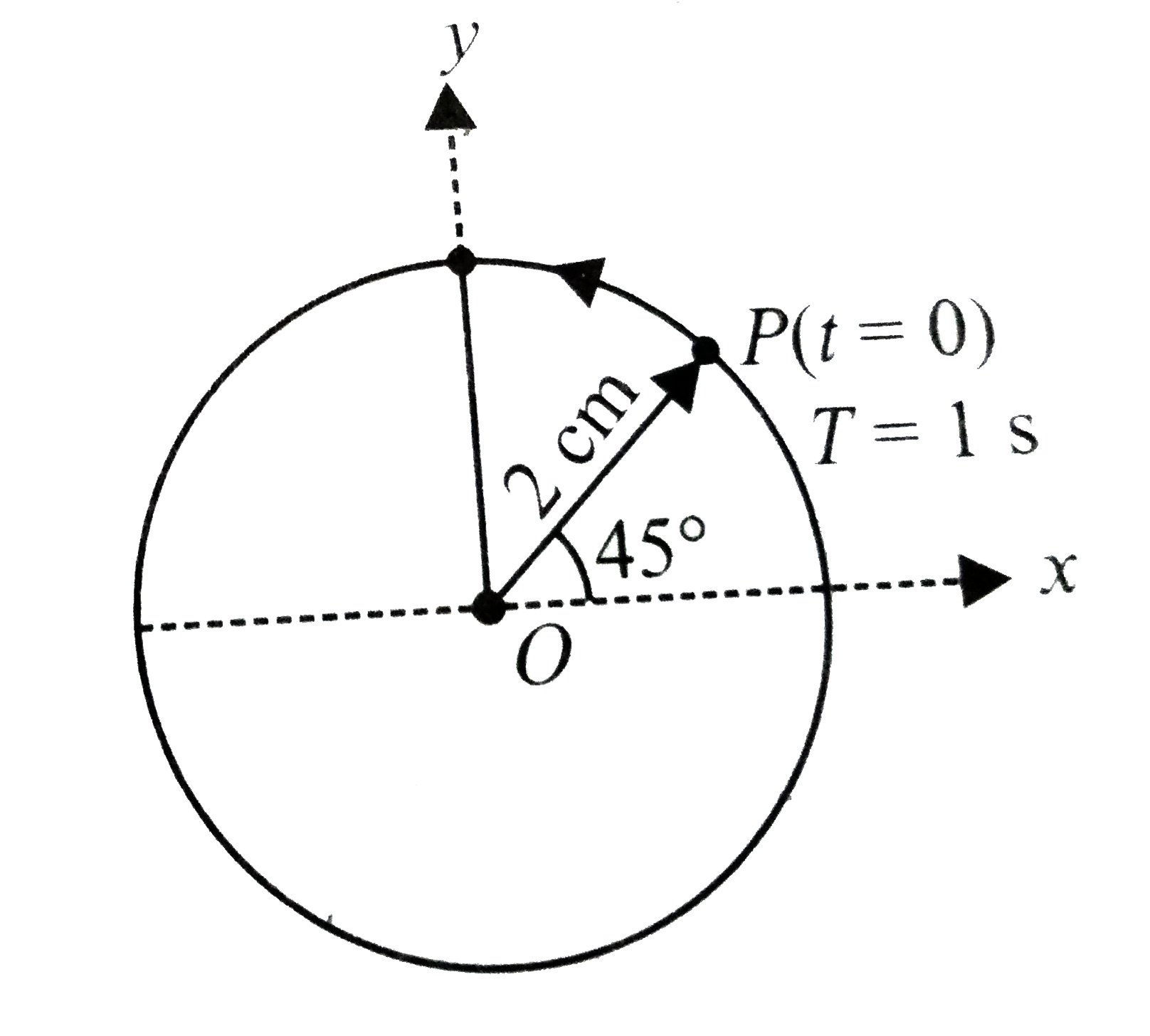
Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial positionn are indicated in the figure. The simple harmonic motion off the x-projection of the radius vector of the rotating particle P is
View SolutionFigure below correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anticlockwise) are indicated on each figure. Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P in each case.
View SolutionFigures,. Correspond to two circular motions. The radius of the circle, the peirod of revolution, the initial position, and the sense of revolution (i.e. clockwise or anticlockwise) are indicated on each. Obtain the corresponding equations of simple harmonic motions of the revolving particle P in each case.
View Solution
