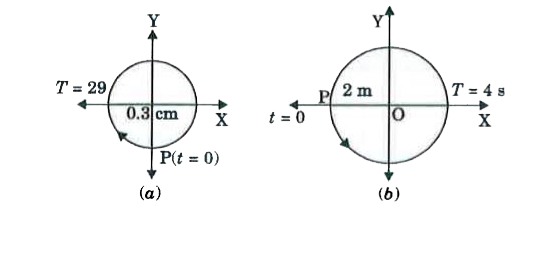
Figures,. Correspond to two circular motions. The radius of the circle, the peirod of revolution, the initial position, and the sense of revolution (i.e. clockwise or anticlockwise) are indicated on each. Obtain the corresponding equations of simple harmonic motions of the revolving particle P in each case.
To solve the problem of obtaining the equations of simple harmonic motion (SHM) for two circular motions based on the provided parameters, we will follow a systematic approach for each case.
Part A:
1. Identify Given Parameters:
- Radius (Amplitude, A) = 3 cm
- Period of revolution (T) = 2 seconds
- Sense of revolution = Clockwise
- Initial position at T = 0: X = 0
2. Calculate Angular Frequency (ω):
ω=2πT=2π2=π rad/s
3. Formulate the General Equation of SHM:
The general equation for SHM is given by:
X(t)=Asin(ωt+ϕ)
4. Determine the Phase Constant (φ):
At T=0, X(0)=0:
0=Asin(ϕ)
Since A≠0, we have:
sin(ϕ)=0⟹ϕ=0 or π
Since the motion is clockwise, we choose ϕ=π.
5. Substitute Values into the SHM Equation:
X(t)=3sin(πt+π)
Using the identity sin(x+π)=−sin(x):
X(t)=−3sin(πt)
Part B:
1. Identify Given Parameters:
- Radius (Amplitude, A) = 2 m
- Period of revolution (T) = 4 seconds
- Sense of revolution = Counterclockwise
- Initial position at T = 0: P=−X
2. Calculate Angular Frequency (ω):
ω=2πT=2π4=π2 rad/s
3. Formulate the General Equation of SHM:
X(t)=Asin(ωt+ϕ)
4. Determine the Phase Constant (φ):
At T=0, X(0)=−X:
−X=Asin(ϕ)
Since A=2:
−2=2sin(ϕ)⟹sin(ϕ)=−1⟹ϕ=3π2
5. Substitute Values into the SHM Equation:
X(t)=2sin(π2t+3π2)
Using the identity sin(x+3π2)=−cos(x):
X(t)=−2cos(π2t)
Final Equations of SHM:
- For Part A:
X(t)=−3sin(πt)
- For Part B:
X(t)=−2cos(π2t)
- Radius (Amplitude, A) = 3 cm
- Period of revolution (T) = 2 seconds
- Sense of revolution = Clockwise
- Initial position at T = 0: X = 0
ω=2πT=2π2=π rad/s
The general equation for SHM is given by:
X(t)=Asin(ωt+ϕ)
At T=0, X(0)=0:
0=Asin(ϕ)
Since A≠0, we have:
sin(ϕ)=0⟹ϕ=0 or π
Since the motion is clockwise, we choose ϕ=π.
X(t)=3sin(πt+π)
Using the identity sin(x+π)=−sin(x):
X(t)=−3sin(πt)
- Radius (Amplitude, A) = 2 m
- Period of revolution (T) = 4 seconds
- Sense of revolution = Counterclockwise
- Initial position at T = 0: P=−X
ω=2πT=2π4=π2 rad/s
X(t)=Asin(ωt+ϕ)
At T=0, X(0)=−X:
−X=Asin(ϕ)
Since A=2:
−2=2sin(ϕ)⟹sin(ϕ)=−1⟹ϕ=3π2
X(t)=2sin(π2t+3π2)
Using the identity sin(x+3π2)=−cos(x):
X(t)=−2cos(π2t)
- For Part A:
X(t)=−3sin(πt)
- For Part B:
X(t)=−2cos(π2t)
Topper's Solved these Questions
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Additional Exercises
6 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - NCERT CHAPTER
26 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Advanced Problems For Competitions
20 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
Similar Questions
An air chamber of volume V has a neck area of cross section A into which a ball of mass m just fits and can move up and down without any friction, figure. Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time periodof oscillations assuming pressure volume variatinos of air to be isothermal.
View SolutionA string of mass 2.50kg is under a tension os 200N. The length of the stretched string is 20.0m. If the transverse jerk is struck at one end of the string, how long does the disturbance take to reach the other end?
View SolutionA particle is performing simple harmonic motion of period T about a point O and it passes through a point P, where OP=y with velicity v in the direction →OP. Show that the time which elapses before it returns to P again is
(T/π)tan−1(vT2πy)
View Solution(a+b)2+(a−b)2=….
View SolutionAssertion : Number of significant figure in 0.005 is one and that is 0.500 is three
Reason : This is became zeros are not significant
View Solutiondepict two circulat mothions. The radius of the circle, the period of revolution, the initial position and sense of revolution are indicated in the figures. Obtain the simple harmonic motinosof the x-projection of the radius vector of the rotating particle P in each case.
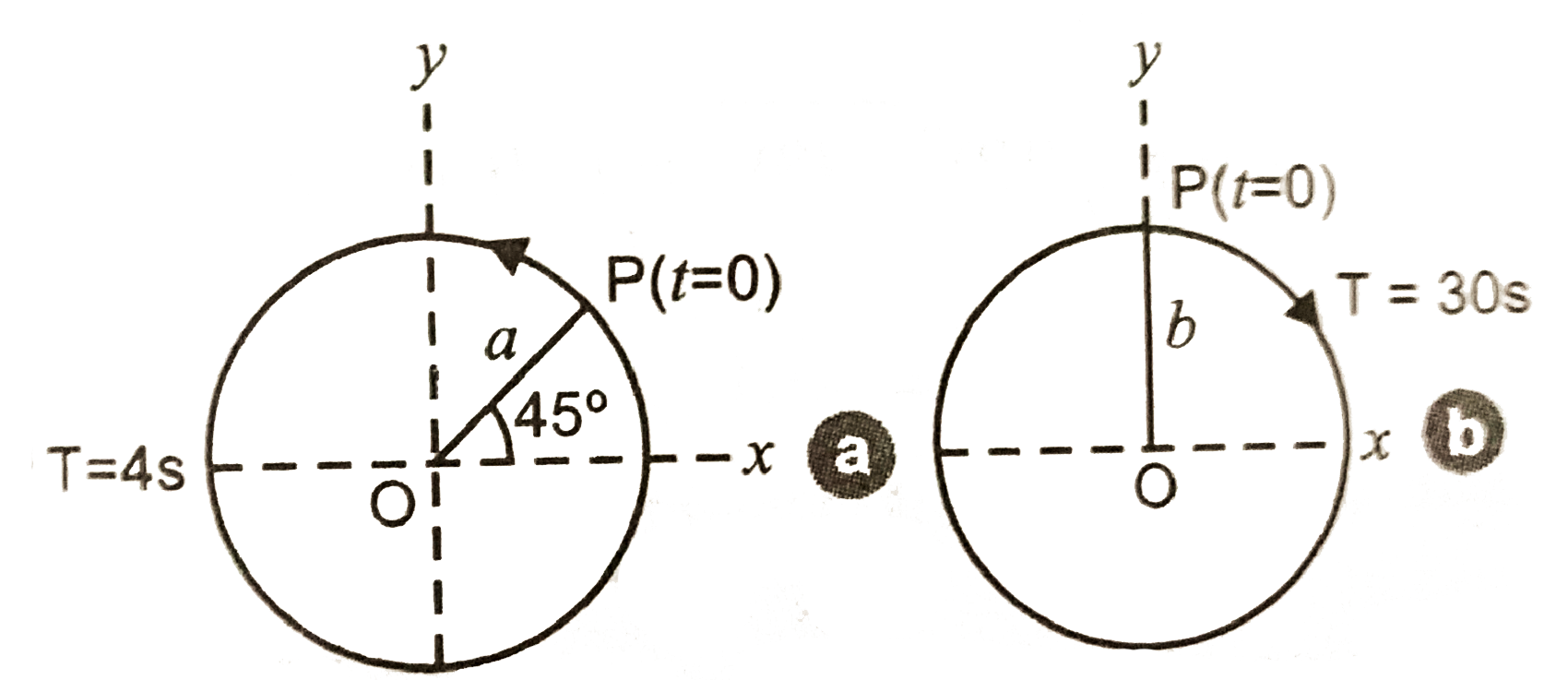
View Solutionthe circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is
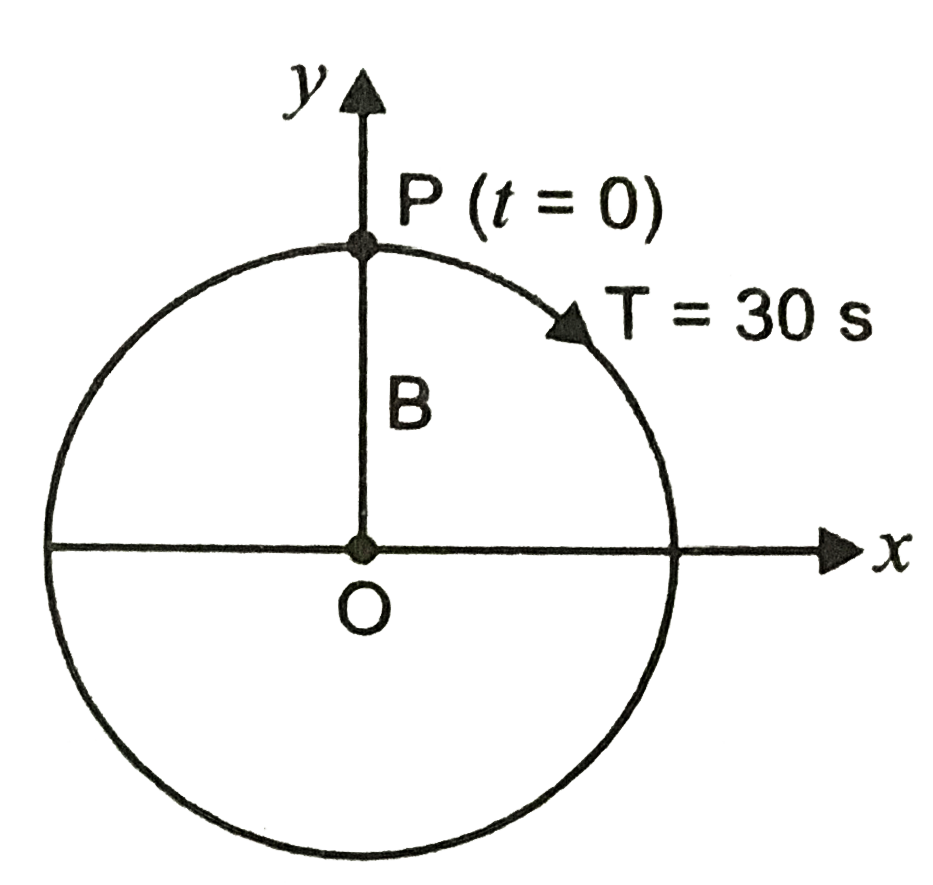
View Solution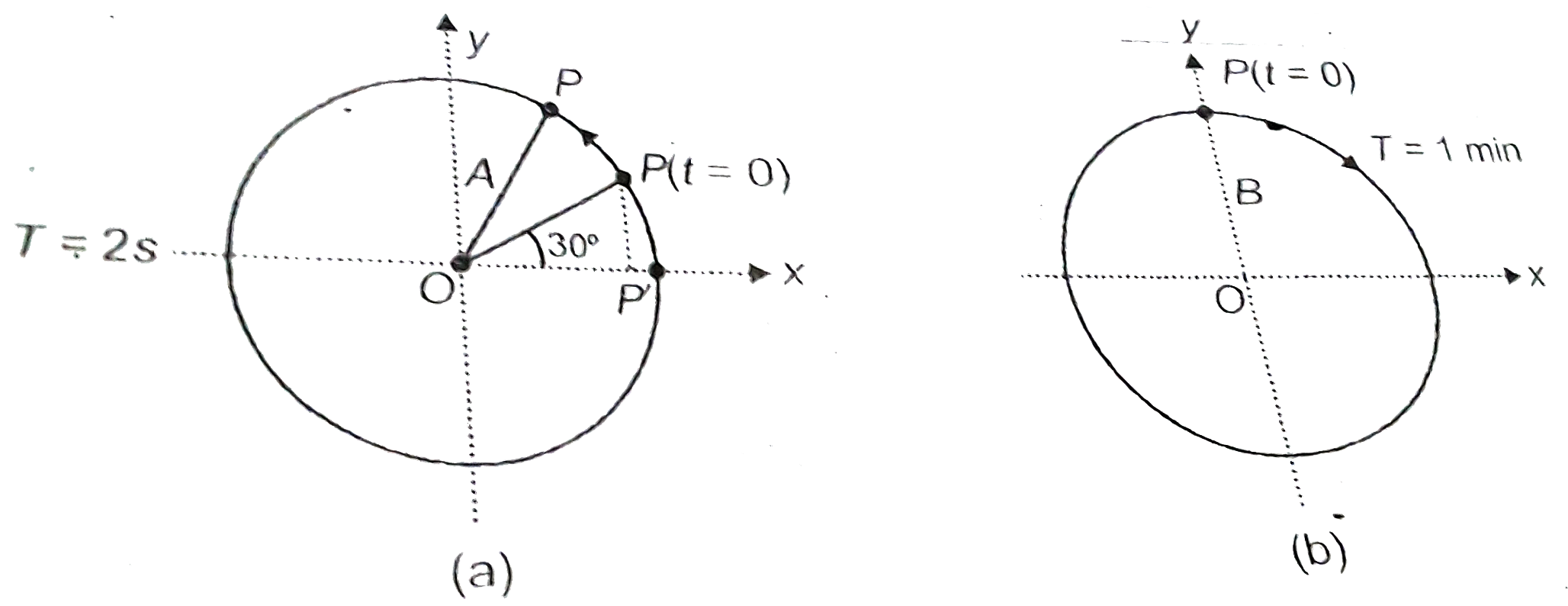
Figure depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figure. Obtain the SHMs of the x-projection of the radius vector of the rotating particle P in each case.
View SolutionFigure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated in the · figure. The simple harmonic motion of the X-projection of the radius vector of the rotating particle Pis
View SolutionFigure below correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anticlockwise) are indicated on each figure. Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P in each case.
View SolutionThe figure given below depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated in the figures. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in each case.

View SolutionFigures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.
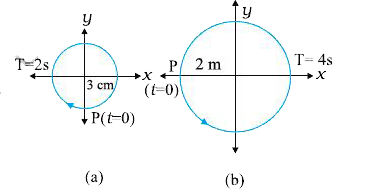
Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
View SolutionFigures depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figures. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in each case.
View SolutionFigures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.
View SolutionFigures depicts two circular motions. The radius of the circle, the period of revolution, the initial position and the sense of revolution are indicated on the figures. Obtain the simple harmonic motions of the x-projection of the radius vector of the rotating particle P in each case.

View Solution
