Displacement-time equation of a particle moving along x-axis is x=20+t3−12t (SI units)
(a) Find, position and velocity of particle at time t=0.
(b) State whether the motion is uniformly accelerated or not.
(c) Find position of particle when velocity of particle is zero.
12m/s
22m/s
−22m/s
−12m/s
The correct Answer is:D
(a) x=20+t3−12t …(i)
At t=0, x=20+0−0=20m
Velocity of particle at time t can be obtained by differentiating Eq. (i) w.r.t. time i.e.
v=dxdt=3t2−12 …(ii)
At t=0, v=0−12=−12m/s
(b) Differentiating Eq. (ii) w.r.t. time t, we get the acceleration a=dvdt=6t
As acceleration is a function of time, the motion is non-uniformly accelerated.
(c) Substituting v=0 in Eq. (ii), we have 0=3t2−12
Positive value of t comes out to be 2s from this equation. Substituting t=2s in
Eq. (i), we have x=20+(2)3−12(2) or x=4m
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 11videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 21videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
The displacement -time equation of a particle moving along x -axis is x=t33−t22+20The acceleration -velocity equation of the particle is a2=KV+1 Then the value of K is
View SolutionThe displacement x of a particle varies with time as x=4t2–15t+25. Find the position, velocity and acceleration of the particle at t = 0.
View Solution
Knowledge Check
- Question 1 - Select One
The position of a particle moving along x-axis given by x=(−2t3−3t2+5)m. The acceleration of particle at the instant its velocity becomes zero is
A12m/s2B−12m/s2C−6m/s2DZero - Question 2 - Select One
If the velocity of the a particle moving on x-axis is given by v=3t2−12t+6. at what time is the acceleration of particle zero ?
A2 secB2+√2secC2−√2secDzero - Question 3 - Select One
The acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
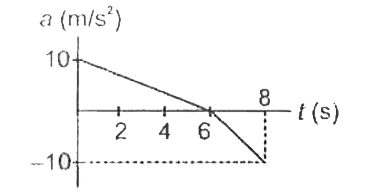 A+15m/sB+20m/sC−15m/sD−20m/s
A+15m/sB+20m/sC−15m/sD−20m/s
The position of the particle moving along x-axis is given by x=2t−3t2+t3 where x is in mt and t is in second.The velocity of the particle at t=2sec is
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionFor a particle moving along x-axis, velocity-time graph is as shown in figure. Find the displacement of the particle?
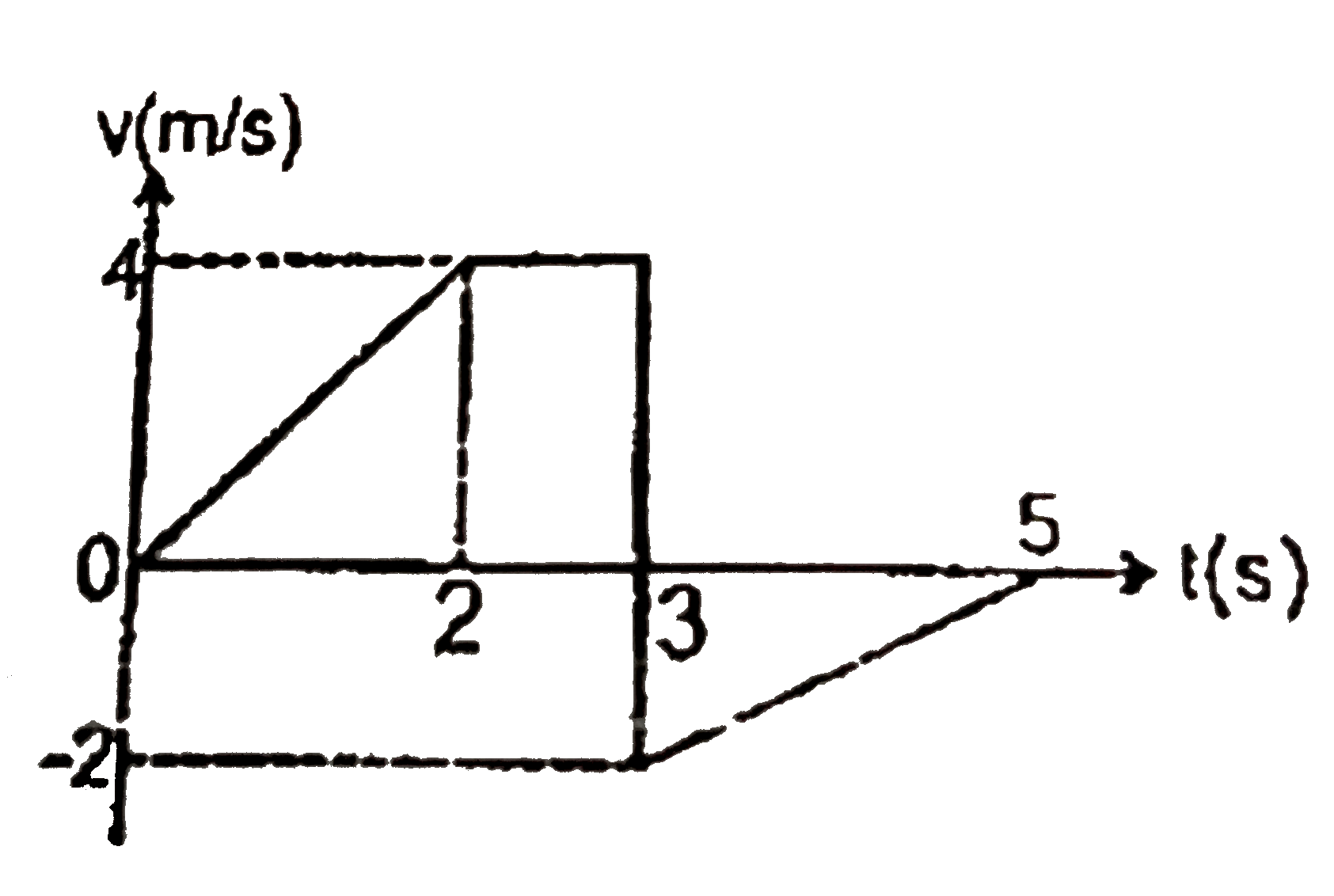 View Solution
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
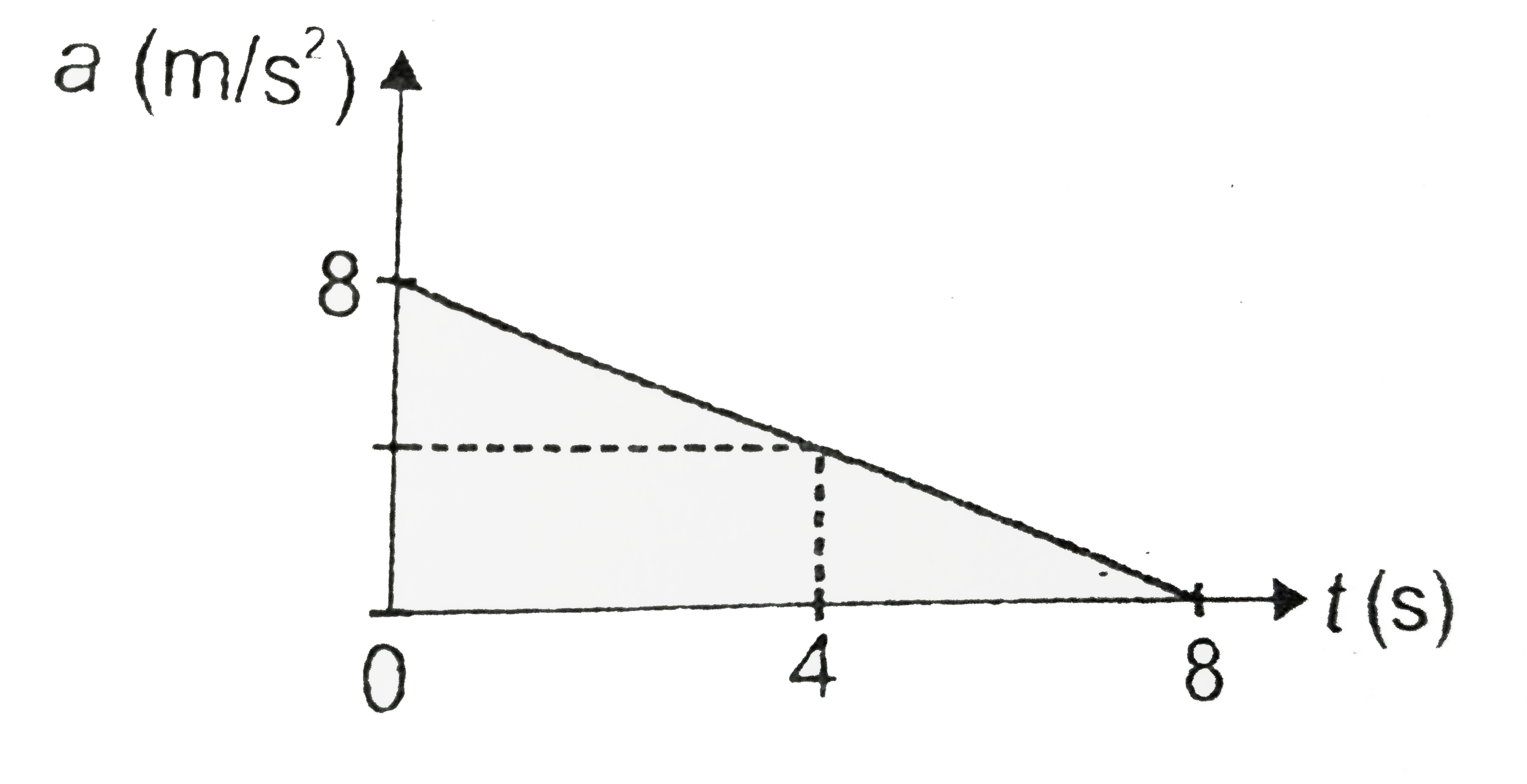 View Solution
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
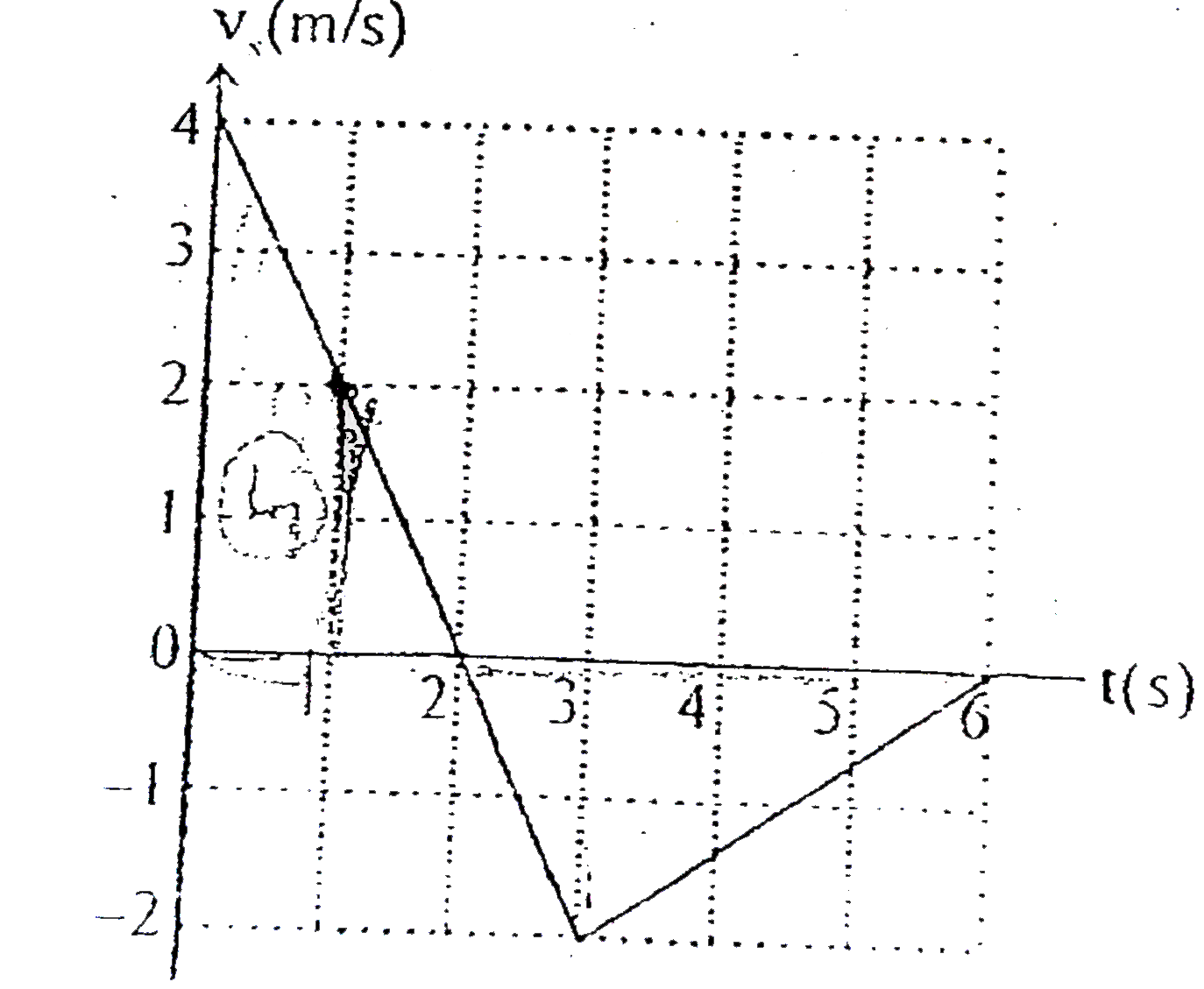 View Solution
View Solution

