Velocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
To solve the problem, we need to find the displacement of a particle at time t=2 seconds, given that its velocity varies with displacement as v=√4+4s.
1. Write the given equation for velocity:
v=√4+4s
2. Square both sides to eliminate the square root:
v2=4+4s
3. Rearrange the equation to express displacement s in terms of velocity v:
4s=v2−4⟹s=v2−44
4. Use the relationship between velocity, acceleration, and displacement:
We know from kinematics that:
v2=u2+2as
Here, u is the initial velocity and a is the acceleration.
5. Identify the initial conditions:
At t=0, s=0. Since we need to find u (initial velocity) and a (acceleration), we can substitute s=0 into our rearranged equation:
v2=4+4(0)=4⟹v=2m/s
Thus, the initial velocity u=2m/s.
6. Find acceleration a:
From the equation v2=4+4s, we can see that the term 4s indicates a constant acceleration. By differentiating v with respect to s:
dvds=dds(√4+4s)=42√4+4s=2√4+4s
The acceleration a can be derived from a=vdvds:
a=v⋅2√4+4s=2√4+4s√4+4s=2m/s2
7. Use the second equation of motion to find displacement at t=2 seconds:
s=ut+12at2
Substituting u=2m/s, a=2m/s2, and t=2s:
s=2⋅2+12⋅2⋅(22)
s=4+12⋅2⋅4=4+4=8meters
Final Answer:
The displacement of the particle at t=2 seconds is s=8meters.
v=√4+4s
v2=4+4s
4s=v2−4⟹s=v2−44
We know from kinematics that:
v2=u2+2as
Here, u is the initial velocity and a is the acceleration.
At t=0, s=0. Since we need to find u (initial velocity) and a (acceleration), we can substitute s=0 into our rearranged equation:
v2=4+4(0)=4⟹v=2m/s
Thus, the initial velocity u=2m/s.
From the equation v2=4+4s, we can see that the term 4s indicates a constant acceleration. By differentiating v with respect to s:
dvds=dds(√4+4s)=42√4+4s=2√4+4s
The acceleration a can be derived from a=vdvds:
a=v⋅2√4+4s=2√4+4s√4+4s=2m/s2
s=ut+12at2
Substituting u=2m/s, a=2m/s2, and t=2s:
s=2⋅2+12⋅2⋅(22)
s=4+12⋅2⋅4=4+4=8meters
The displacement of the particle at t=2 seconds is s=8meters.
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Exercise 6.1
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Exercise 6.2
3 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Example Type 7
1 Video
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Velocity of a particle moving in a straight line varies with its displacement as v=√4+4xm/s where x is displacement. Displacement of particle at time t = 0 is x = 0. Find displacement (in m) of particle in 2 sec.
View SolutionA particle is moving in a straight line and its velocity varies with its displacement as v=√4+4s m/s. Assume s=0 at t=0. find the displacement of the particle in metres at t=1s.
View Solution
Knowledge Check
For a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
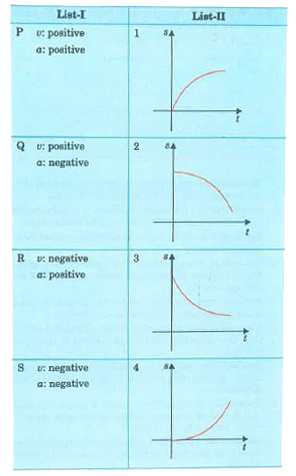 APQRS3241BPQRS1324CPQRS2134DPQRS4132
APQRS3241BPQRS1324CPQRS2134DPQRS4132
Velocity-time graph of a particle moving in a straight line is shown in figure. At time t=0, displacement of the particle from mean position is 10 m. Find
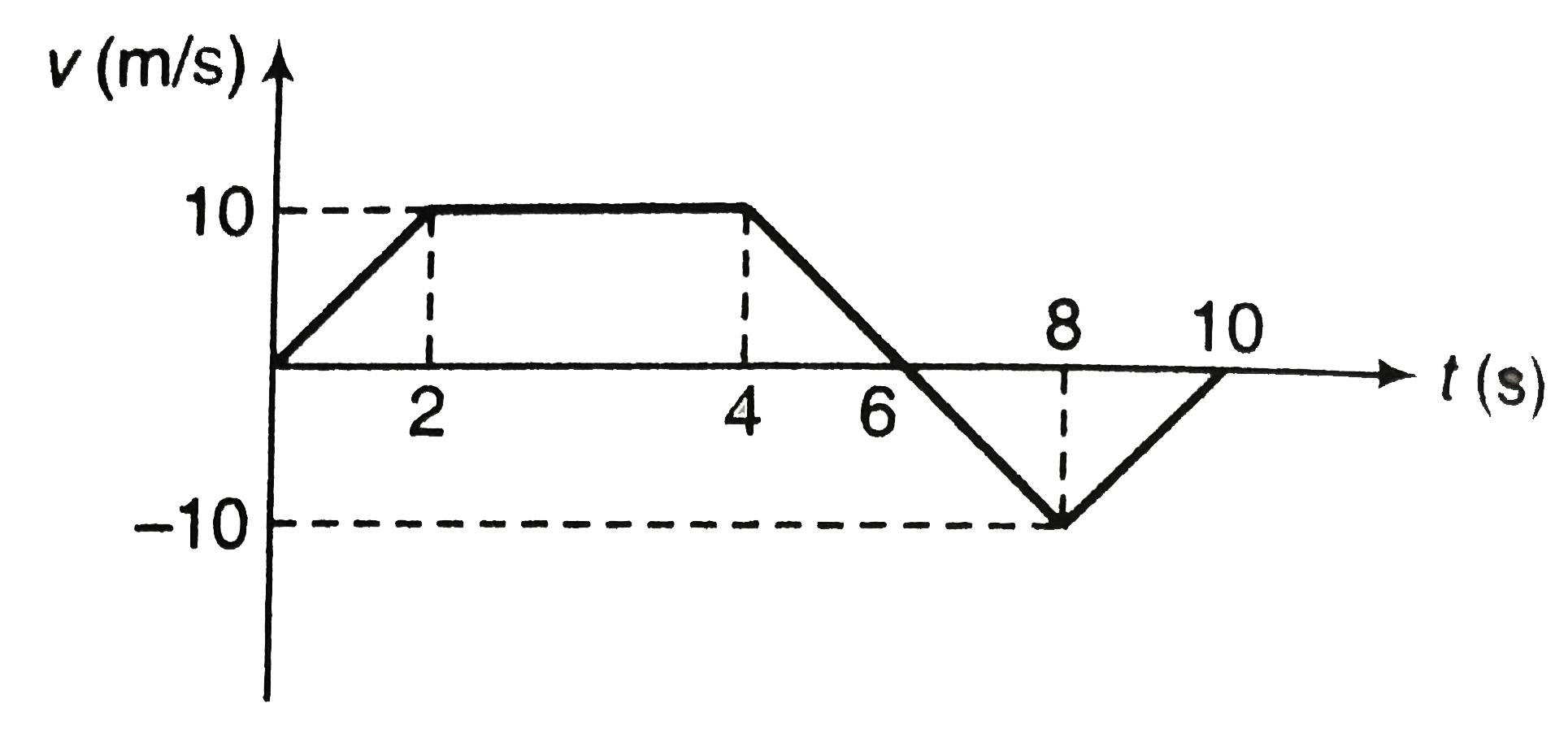
(a) acceleration of particle at t=1s,3sand9s.
(b) position of particle from mean position at t=10s.
(c) write down s-t equation for time interval (i)0≤t≤2s, (ii) 4s≤t≤8s
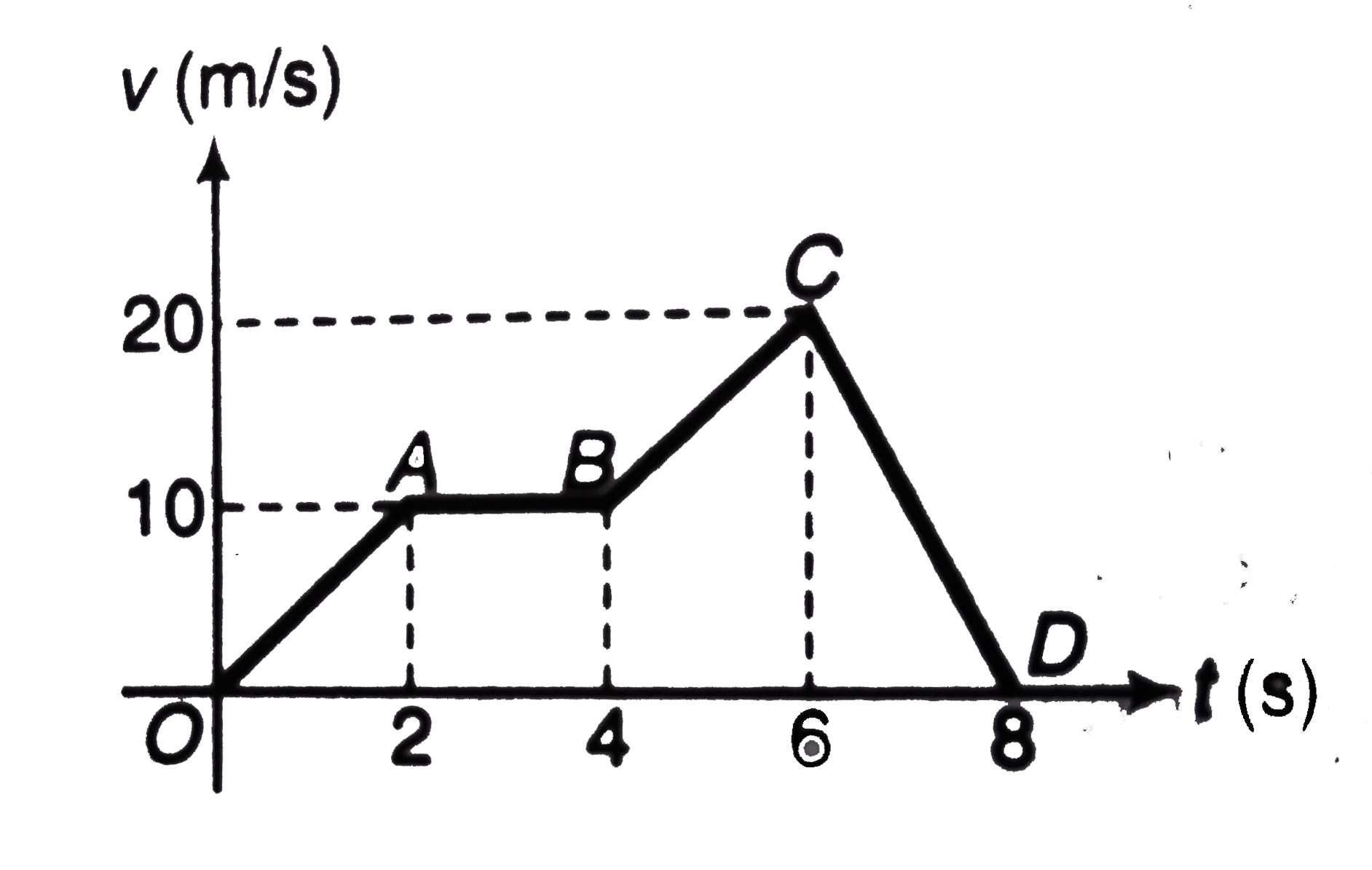
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. Plot the corresponding displacement-time graph of the particle if at time t=0, displacement s=0.
View SolutionThe acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (S) as a=2S. The velocity of the particle is zero and zero displacement. Find the corresponding velocity-displacement equation.
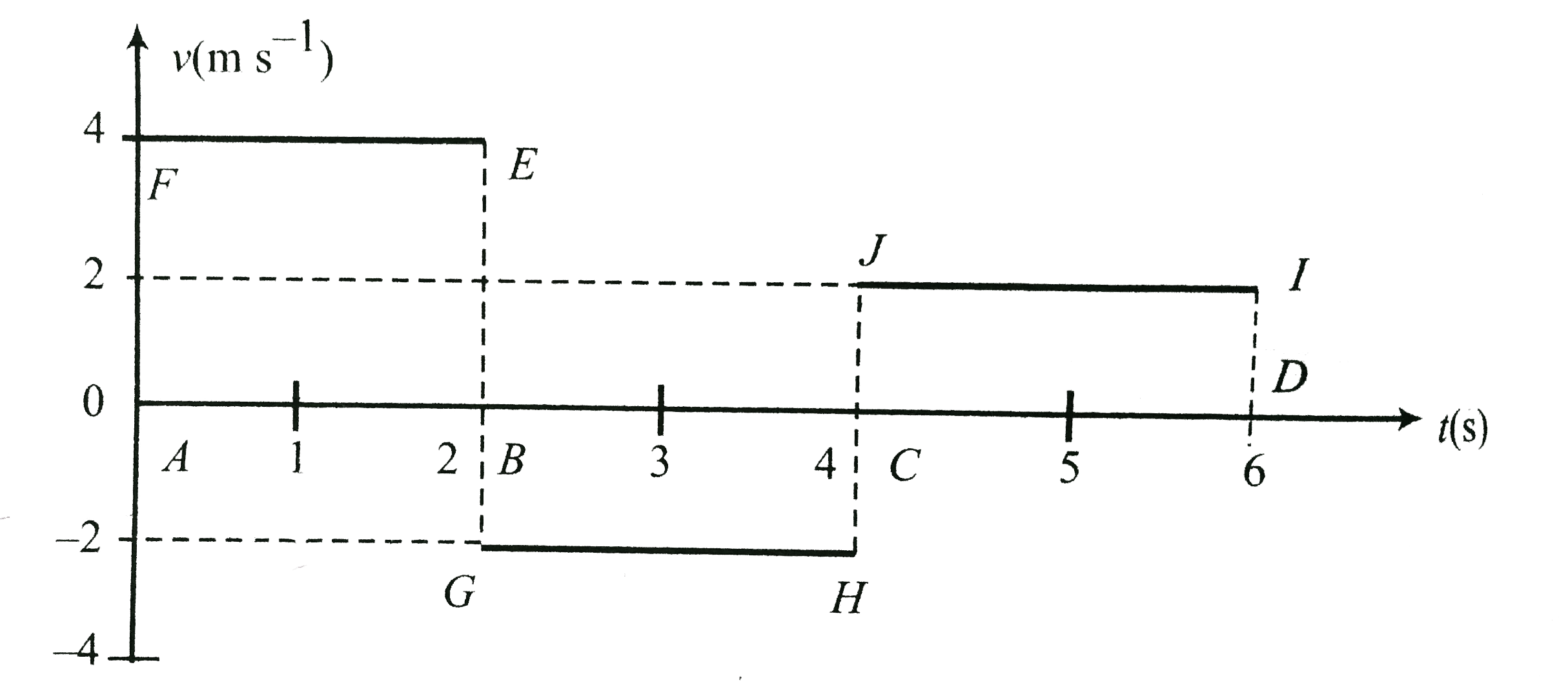
View SolutionThe velocity-time graph of a particle moving in a staight line is shown in the . Find the displacement and the distance trav elled by the particle in 6s.
 .
.
View SolutionVelocity-time equation of a particle moving in a straight line is, v=(10+2t+3t2) (SI units) Find
(a) displacement of particle from the mean position at time t=1s, if it is given that displacement is 20m at time t=0.
(b) acceleration-time equation.
View SolutionIf the velocity v of a particle moving along a straight line decreases linearly with its displacement from 20m/s to a value approaching zero at s=30m, determine the acceleration of the particle when s=15m.
View Solution