A particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
To determine whether the statement "The average velocity of the particle in this time interval is (v_1 + v_2)/2" is true or false, we can analyze the motion of the particle under uniform acceleration.
1. Understanding Uniform Acceleration:
A particle moving with uniform acceleration means that its velocity changes at a constant rate. The initial velocity at time t=0 is v1 and the velocity at time t is v2.
2. Using the Equation of Motion:
The equation for velocity under uniform acceleration is given by:
v=u+at
where v is the final velocity, u is the initial velocity, a is the acceleration, and t is the time. Here, u=v1 at t=0 and v=v2 at t.
3. Finding Average Velocity:
The average velocity vavg over a time interval can be calculated as:
vavg=v1+v22
This is valid for uniformly accelerated motion because the velocity changes linearly over time.
4. Conclusion:
Since we have shown that the average velocity for a particle moving with uniform acceleration between two points in time is indeed given by the arithmetic mean of the initial and final velocities, we conclude that the statement is true.
Final Answer:
The statement is True.
A particle moving with uniform acceleration means that its velocity changes at a constant rate. The initial velocity at time t=0 is v1 and the velocity at time t is v2.
The equation for velocity under uniform acceleration is given by:
v=u+at
where v is the final velocity, u is the initial velocity, a is the acceleration, and t is the time. Here, u=v1 at t=0 and v=v2 at t.
The average velocity vavg over a time interval can be calculated as:
vavg=v1+v22
This is valid for uniformly accelerated motion because the velocity changes linearly over time.
Since we have shown that the average velocity for a particle moving with uniform acceleration between two points in time is indeed given by the arithmetic mean of the initial and final velocities, we conclude that the statement is true.
The statement is True.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Exercise 6.65videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Exercise 6.73videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - Exercise 6.42videos
KINEMATICS
- BOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
A particle move with a velocity v=αt3 along a straight line.The average velocity in time interval t=0 to t=T is
View SolutionA particle moves in a straight line with an acceleration a ms−2 at time 't' seconds where a =−1t2. When t = 1 the particle has a velocity of 3ms−1 then the velocity when t = 4 is v4. Find the value of v.
View Solution
Knowledge Check
- Question 1 - Select One
For body moving with uniform acceleration a, initial and final velocities in a time interval t are u and v respectively. Then its average velocity in the time interval t is
A(v+at)B(v−at2)C(v−at)D(u−at2) - Question 2 - Select One or More
A particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
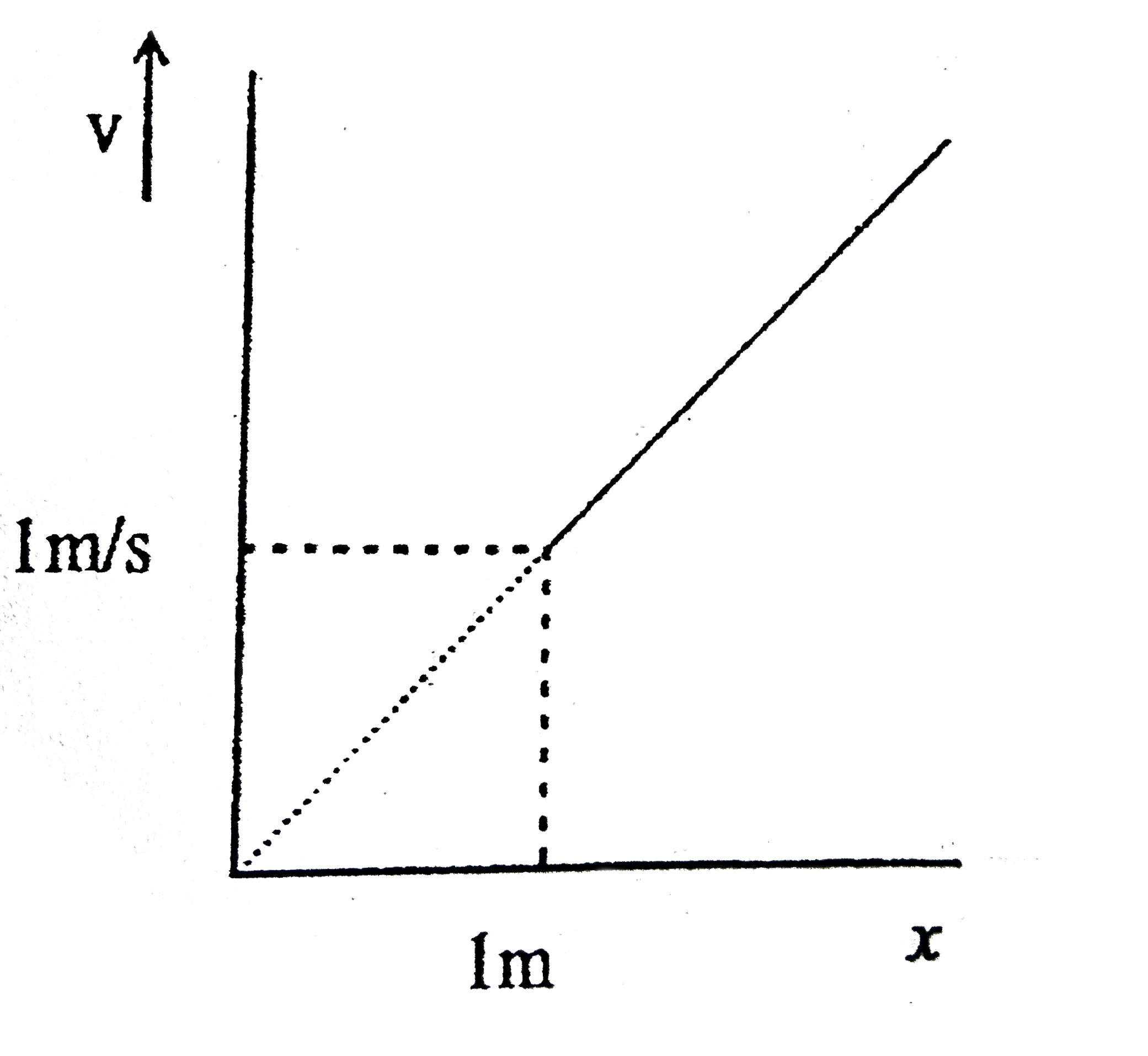 A
A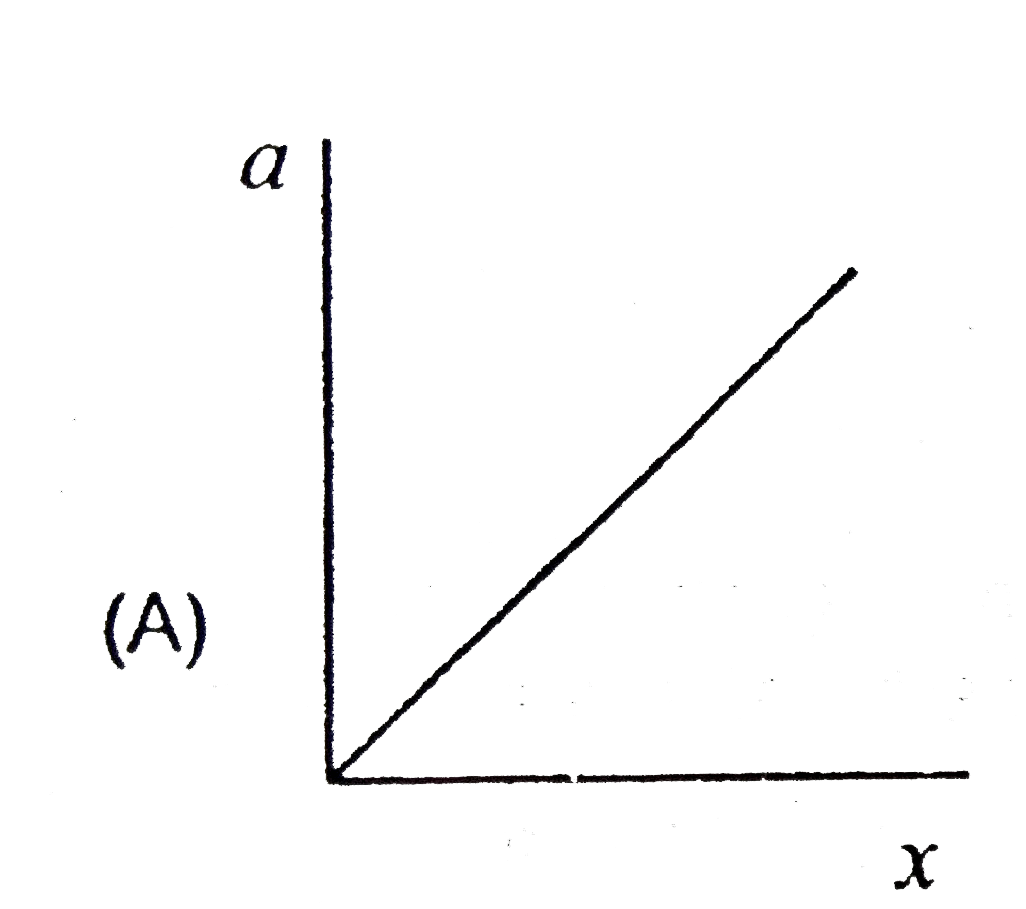 B
B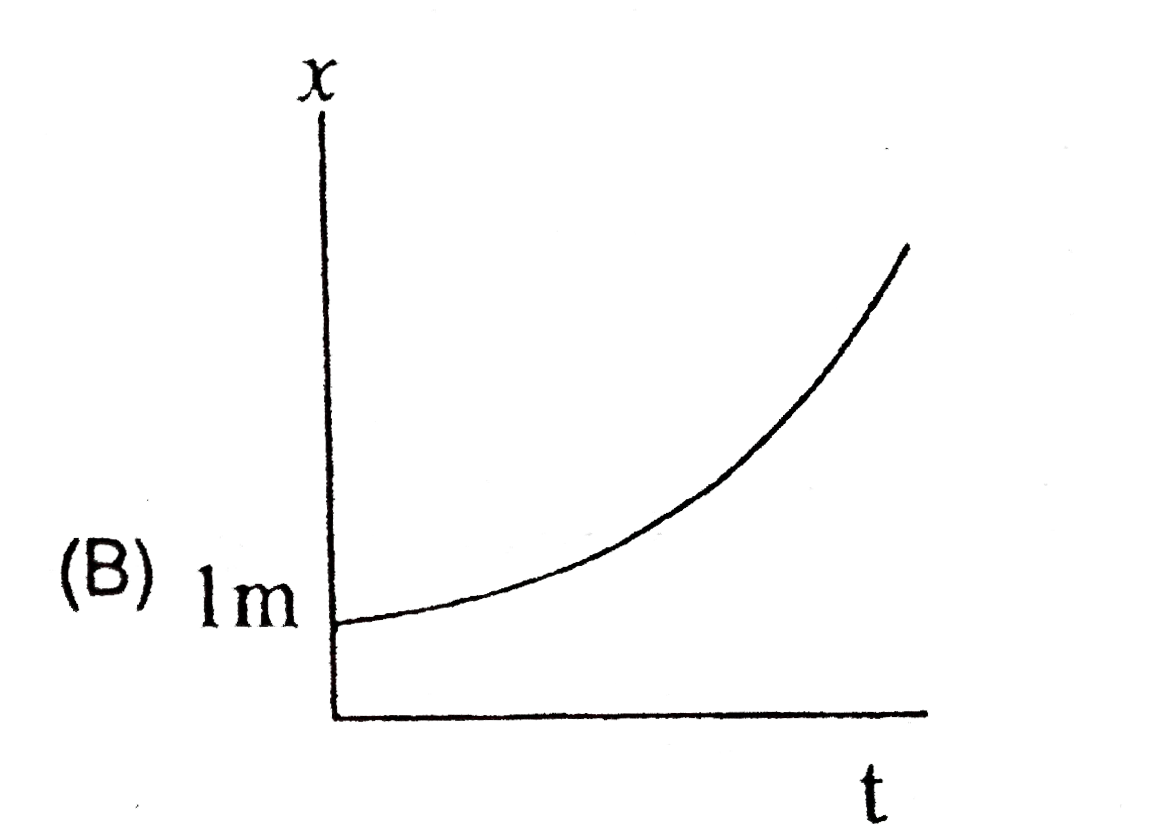 C
C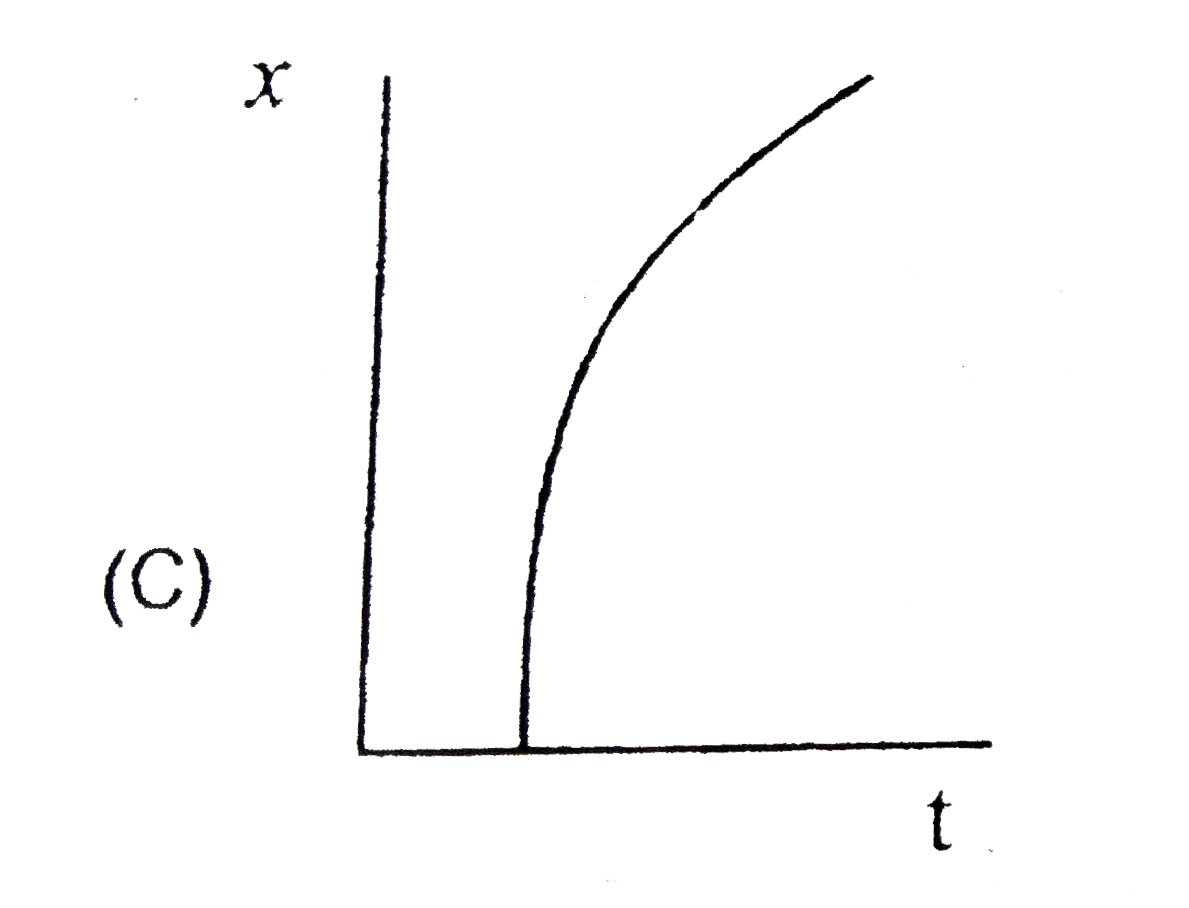 D
D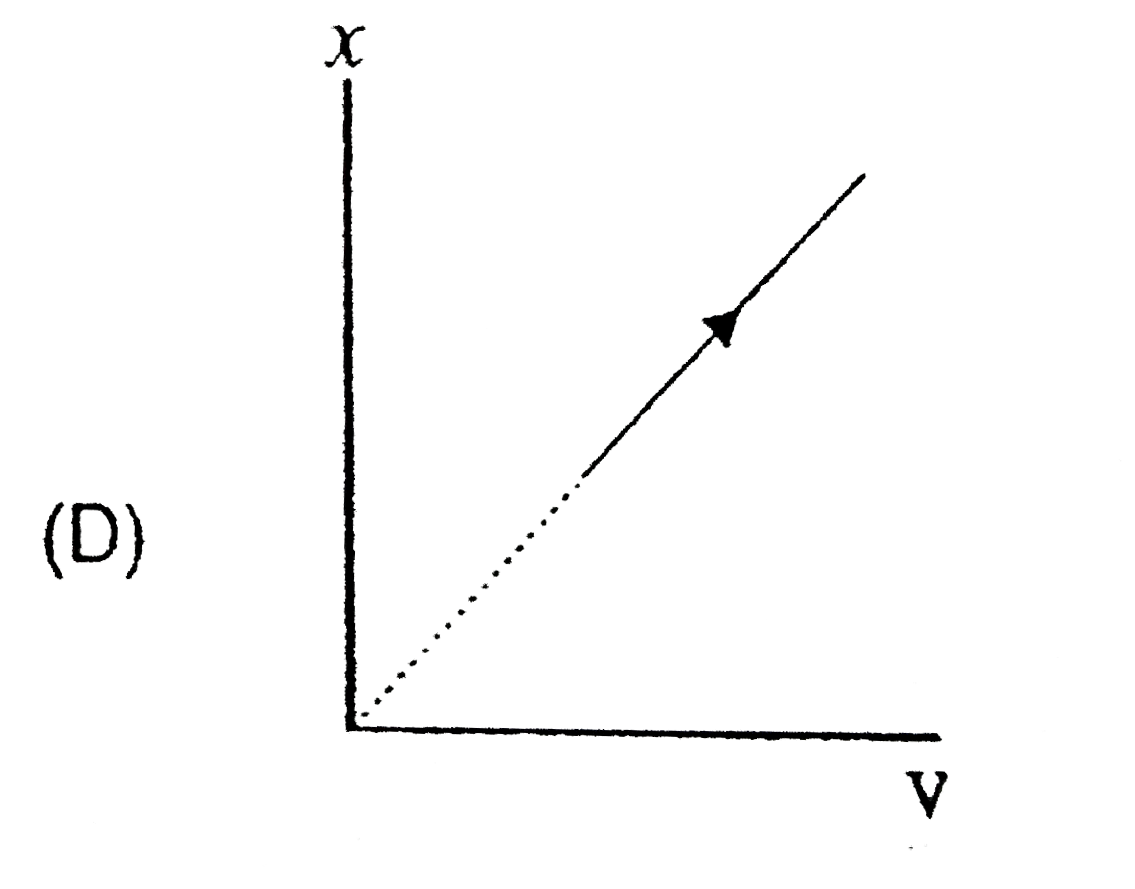
- Question 3 - Select One or More
A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
AAverage velcotu is 25/3ms−1BAverage speed is 10ms−1.CAverage velcotu is 5/3ms−1DAcceleration is 4ms−2 at t=o
A particle moves with a velocity v(t)=(12)kt2 along a straight line . Find the average speed of the particle in a time t.
View SolutionA particle moves along a straight line. Its velocity and speed are denoted by v1 and v2. The quantity v1v2
View SolutionA particle moves from A to B with a uniform velocity v1 and from B to A with a velocity v2. If it moves along a straight line between A and B, then the average velocity of the particle is
View SolutionIf velocity of a particle is given by v=(2t+3)m/s. Then average velocity in interval 0≤t≤1 s is :
View SolutionStatement-I : A particle moves in a straight line with constant acceleration. The average velocity of this particle cannot be zero in any time interval.
Statement-II : For a particle moving in straight line with constant acceleration, the average velocity in a time interval is u+v2, where u and v are initial and final velocity of the particle of the given time interval.View Solution

