A particle moves along a straight line. Its velocity and speed are denoted by v1 and v2. The quantity v1v2
must be equal to 1
must be equal to -1
can be any positive number
must be either +1 or -1
The correct Answer is:D
Topper's Solved these Questions
Similar Questions
A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
View SolutionA particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
View Solution
Knowledge Check
A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
AAverage velcotu is 25/3ms−1BAverage speed is 10ms−1.CAverage velcotu is 5/3ms−1DAcceleration is 4ms−2 at t=oFor a particle moving along a straight line, its velocity 'v' and displacement 's' are related as v2=cs, here c is a constant. If the displacement of the particle at t=0 is zero, its velocity after 2 sec is:
Ac2s0Bcs0Cc2s−1Dcs−1A particle is executing SHM along a straight line. Its velocities at distances x1 and x2 from the mean position are v1 and v2, respectively. Its time period is
A2π ⎷x21+x22v21+v22B2π ⎷x22−x21v21−v22C2π ⎷v21+v22x21+x22D2π ⎷v21−v22x21−x22
A particle moves in a straight line with uniform acceleration. Its velocity at time t=0 is v1 and at time t=t is v2. The average velocity of the particle in this time interval is v1+v22 . Is this statement true or false?
View SolutionA particle is executing SHM along a straight line. Its velocities at distances x1 and x2 from the mean position are v1 and v2, respectively. Its time period is
View SolutionA particle is executing SHM along a straight line. Its velocities at distances x1 and x2 from the mean position are v1 and v2, respectively. Its time period is
View SolutionA particle moves along a straight line AB with constant acceleration. Its velocities are u and v at A and B, respectively. Show that its velocity at the mid-point of AB is √u2+v22.
View SolutionFigure shows the x-t plot of a particle moving along a straight line. Let v1 and v2, be average speeds in time intervals 1 and 2 respectively. Then
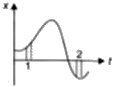
View Solution
