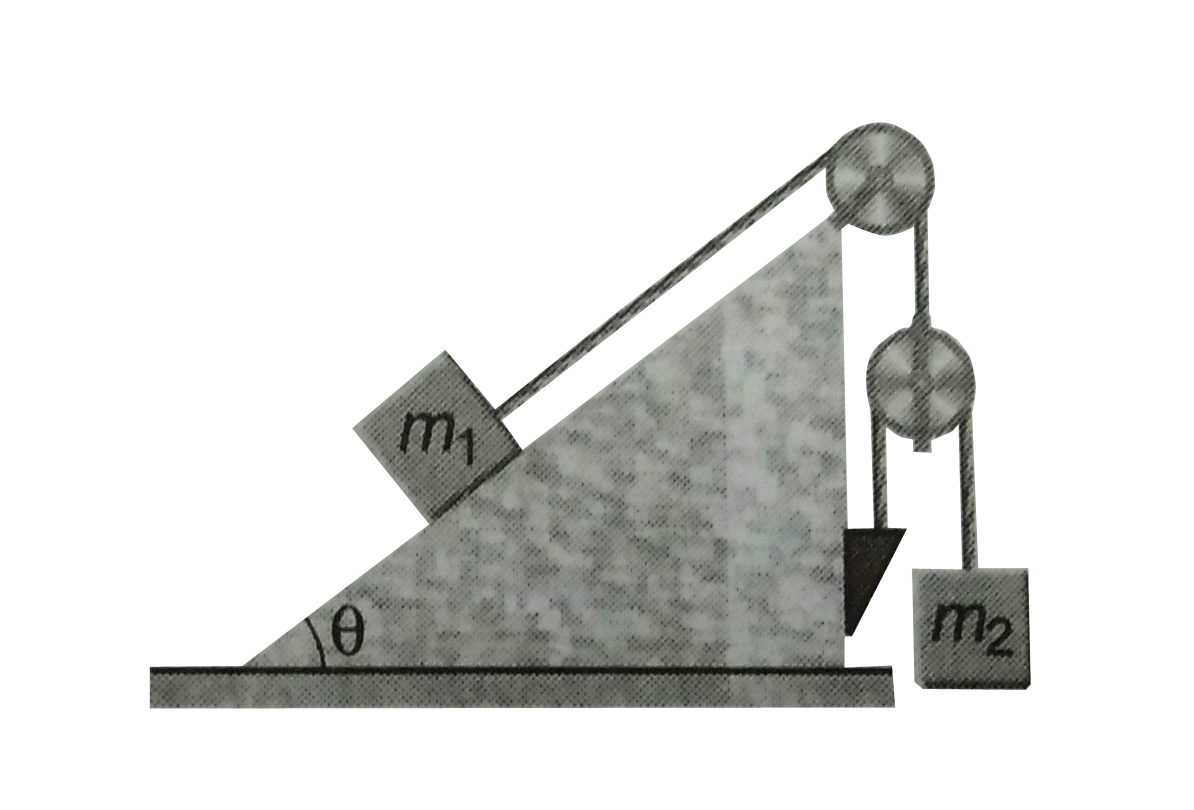
Find the acceleration of the body of mass m2 in the arrangement shown in figure. If the massm2 is η time great as the mass m1 and the angle that the inclined plane forms with the horizontal is equal to θ. The masses of the pulley and threads, as well as the friction, are accumed to be negligible.
g(2η−sinθ)4η+1
2g(η−sinθ)4η+1
2g(2η−sinθ)η+1
2g(2η−sinθ)4η+1
The correct Answer is:D
Here by constraint relation we can see that the acceleration of m2 is two times that of m1 . So we assume if m1 is moving up the inclined plane with an acceleration a, the acceleration of mass m2 going down is 2a. The ten tension in different string are shown in figure.

The dynamic equations can be written as
For mass m1: 2T=m1gsinθ=m1a ...(i)
For mass m2: m2g−T=m2(2a) ...(ii)
Substituting m2=ηm1 and solving Eqs. (i) and (ii), we get
Acceleration of m2=2a=2g(2η−sinθ)4η+1
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.1
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.2
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
Find the acceleration of the prism of mass M and that of the bar of mass m shown in figure.
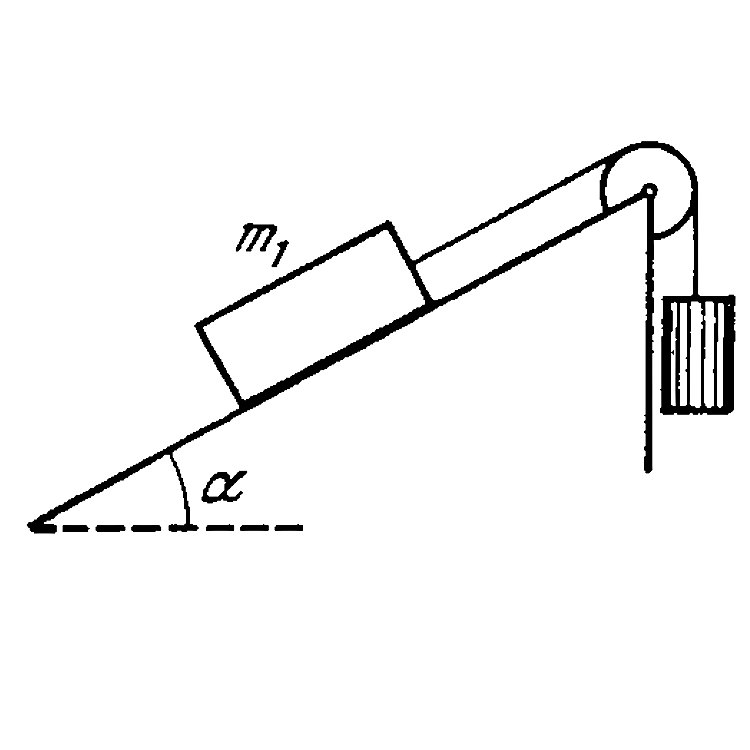
View SolutionFind the acceleration of the block of mass m in the arrangement shown in the following figures. The masses of the pulleys and the threads, as well as the friction are assumed to be negligible.

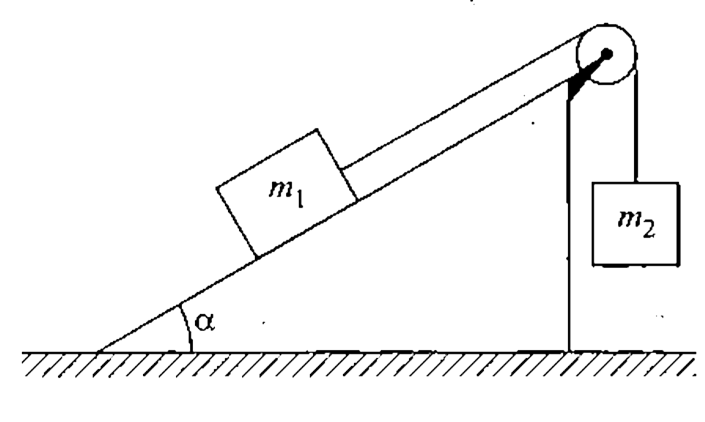
View SolutionThe following parameters of the arrangement of figure are available: the angle α which the inclined plane forms with the horizontal, and the coefficient of friction k between the body m1 and the inclined plane. The masses of the pulley and the threads, as well as the friction in the pulley, are negligible. Assuming both bodies to be motionless at the initial moment, find the mass ratio m2/m1 at which the body m2
(a) starts coming down,
(b) starts going up,
(c) is at rest.
View SolutionFind the accelerations of rod A and wedge B in the arrangement shown in figure if the ratio of the mass of the wedge to that of the rod equals η, and the friction between all contact surfaces is negligible.

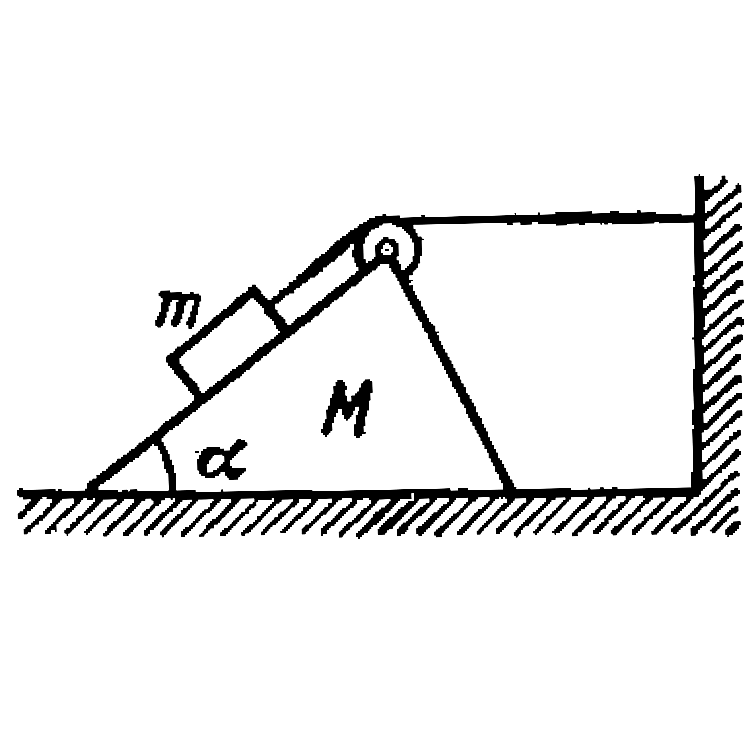
View SolutionIn the arrangement shown in figure the masses m of the bar and M of the wedge, as well as the wedge angle α, are known. The masses of the pulley and the thread are negligible. The friction is absent. Find the acceleration of the wedge M.
View SolutionFind the acceleration of rod A and wedge B in the arrangement shown in figure if the mass of rod equal that of the wedge and the friction between all contact surfaces is negligible Take angle of wedge as 45∘&g=9.8m/s2

View SolutionIn terms of masses m1,m2 and g, find the acceleration of both the blocks shown in Fig. Neglect all friction and masses of the pulley.
View SolutionIn the arrangement shown in fig the bodies have masses m0,m1andm2 the friction is absent the masses of pulleys and the threads are negligible find the acceleration of the body m1

View SolutionIn the arrangement shown in the figure, the blocks have masses 3m,m and 2m, the friction is absent, the masses of the pulleys and the threads are negligible. Find the acceleration of mass 3m.
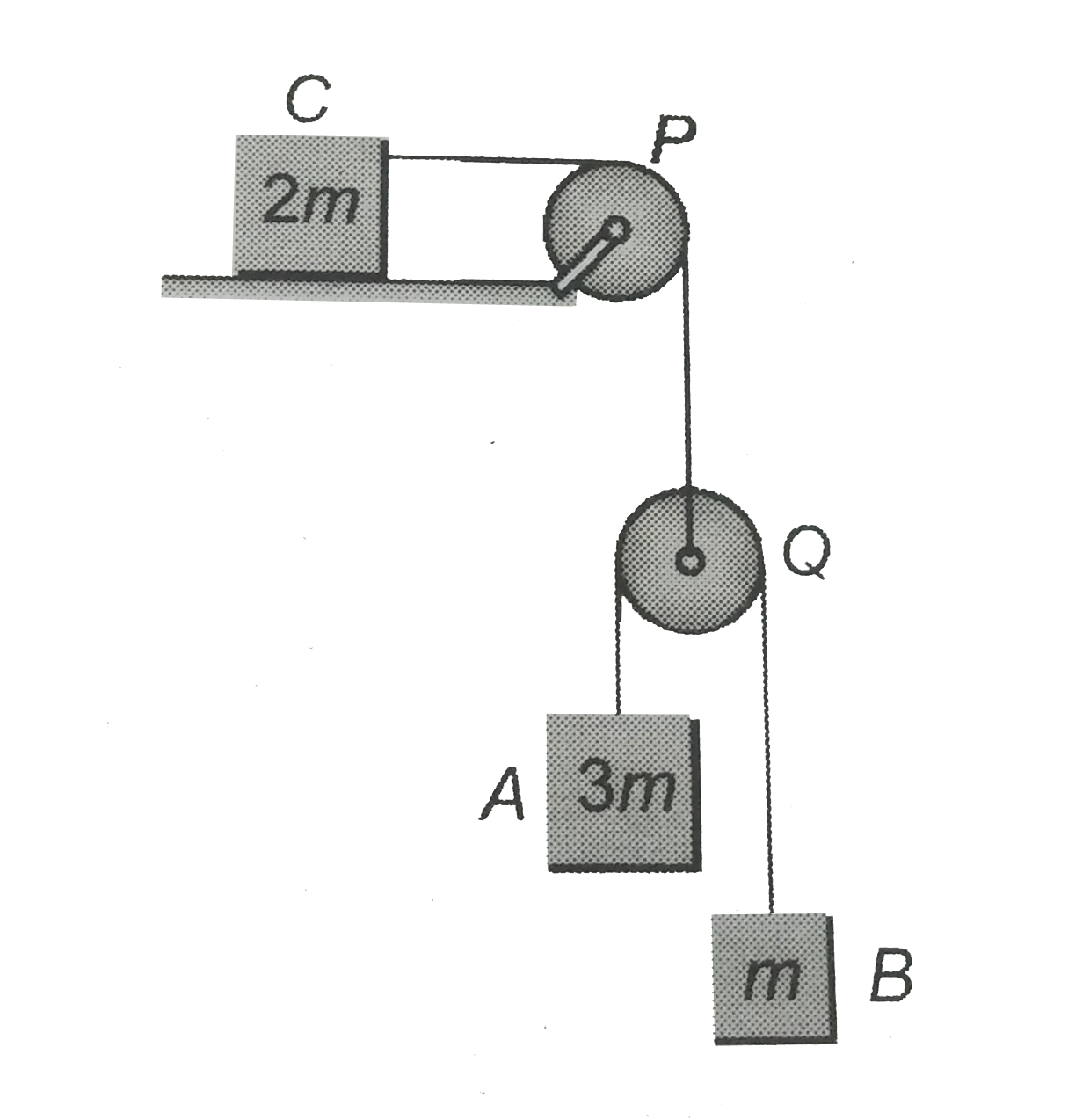
View SolutionFind the acceleration of masses m1 and m2 connected by an inextensible string, shown in figure-2.13(a). The string and pulley are assumed to be massless and frictionless.
View Solution
