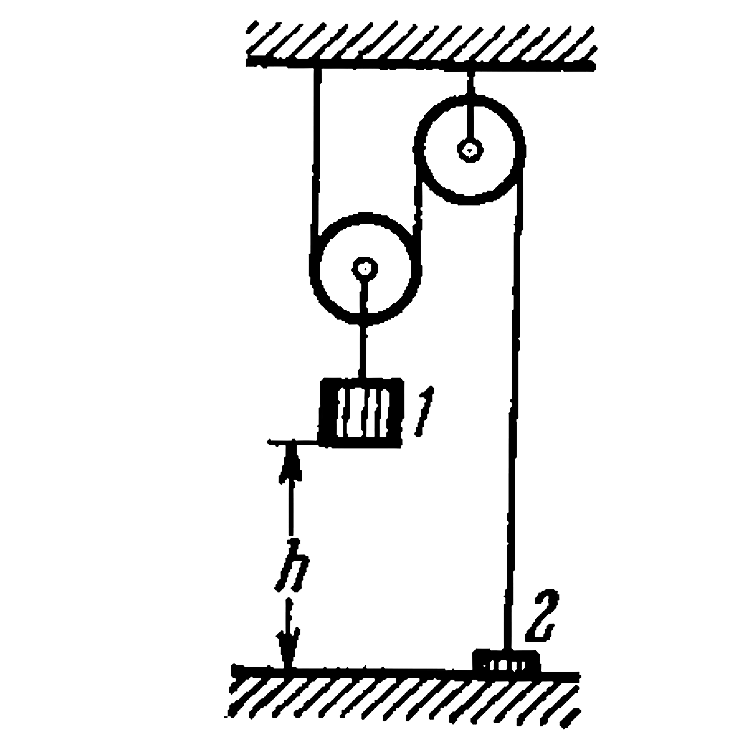
In the arrangement shown in figure the mass of the ball is η times as that of the rod. The length of the rod is L the masses of the pulleys and the threats as well as the friction, are negligible. The ball is set on the same level as the lower and of the rod and then released. How soon will the ball be opposite the upper and of the rod?

From constraint relation we can see that the acceleration of the rod is double then that of the acceleration of the ball .If ball is going up with an acceleration a, rod will be coming down with the acceleration 2a, thus the relative acceleration of the ball with respect to rod is 3a in upward direction. If it takes time t seconds to reach the upper end of the rod, we have
t=√2l3a ...(i)
Let mass of ball be m and that of rod is M the dynamic of these are
For rod Mg−T=M(2a) ...(i)
For rod 2T−mg=ma ...(ii)
Substituting m=ηM and solving Eqs (ii) and (iii), we get
a=(2−ηη+4)g
From Eq (i), we have
t=√2l(η+4)3g(2−η)

Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.1
10 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Exercise 8.2
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery
39 Videos
- KINEMATICS 1BOOK - DC PANDEYCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
In the arrangement shown in fig the mass of the ball 1 is η=1.8 times as great as that of rod 2 The length of the later is l=100 cm The masses of the pulleys and the threads as well as the friction are negligible The ball is set on the same level as the lower end of the rod and then released How soon will the ball be opposite to the other end of the rod

View SolutionIn the arrangement shown in figure the mass of body 1 is η=4.0 times as great as that of body 2. The height h=20cm. The masses of the pulleys and the threads, as well as the friction, are negligible. At a certain moment body 2 is released and the arrangement set in motion. What is the maximum height that body 2 will go up to?
View Solution
Knowledge Check
In the figure , mass of a ball is 95 times mass of the rod, Length of rod is 1m.The level of ball is same as rod level.Find out time taken by the ball to reach at upper end of rod.
 A1.4sB2.45sC3.25 sD5 s
A1.4sB2.45sC3.25 sD5 s

if a mass of ball is m/2 and that of a rod is m the length of the rod is 20 cm the ball is set on the same level as the lower end of the rod and then released. If pulleys and strings are light, friction negligible how soon will the ball be opposite top the upper end of the rod?
View SolutionFind the acceleration of the block of mass m in the arrangement shown in the following figures. The masses of the pulleys and the threads, as well as the friction are assumed to be negligible.

View SolutionIn the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.
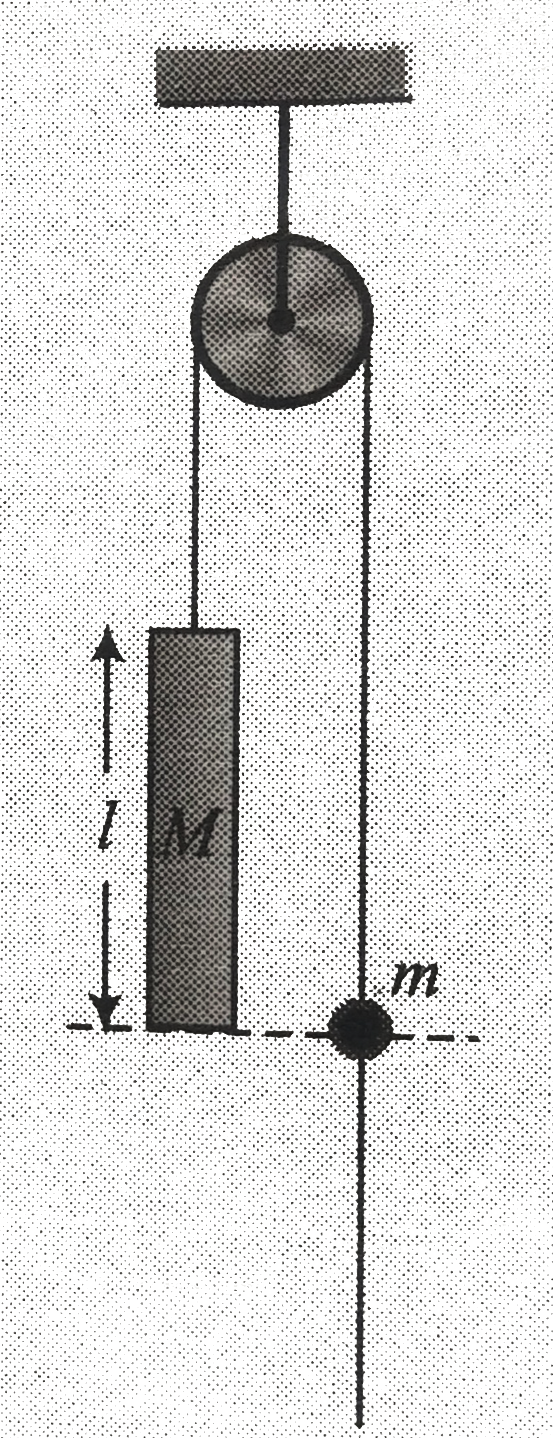
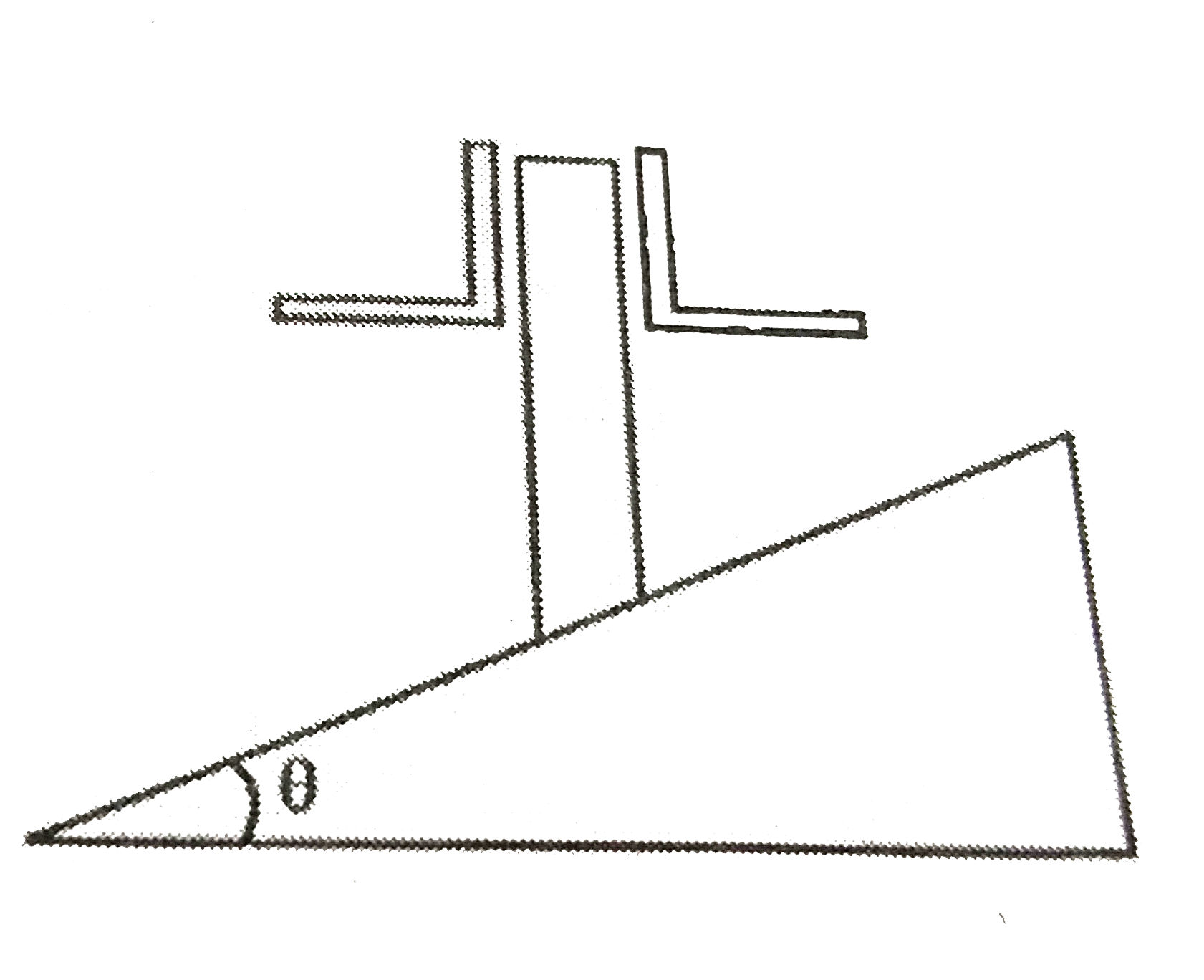
View SolutionFind the accelerations of rod A and wedge B in the arrangement shown in figure if the ratio of the mass of the wedge to that of the rod equals η, and the friction between all contact surfaces is negligible.

View SolutionFind the acceleration of rod A and wedge B in the arrangement shown in fig if the ratio of the mass of wedge to that of the rod equals η and the friction between the contact surfaces are negligible.
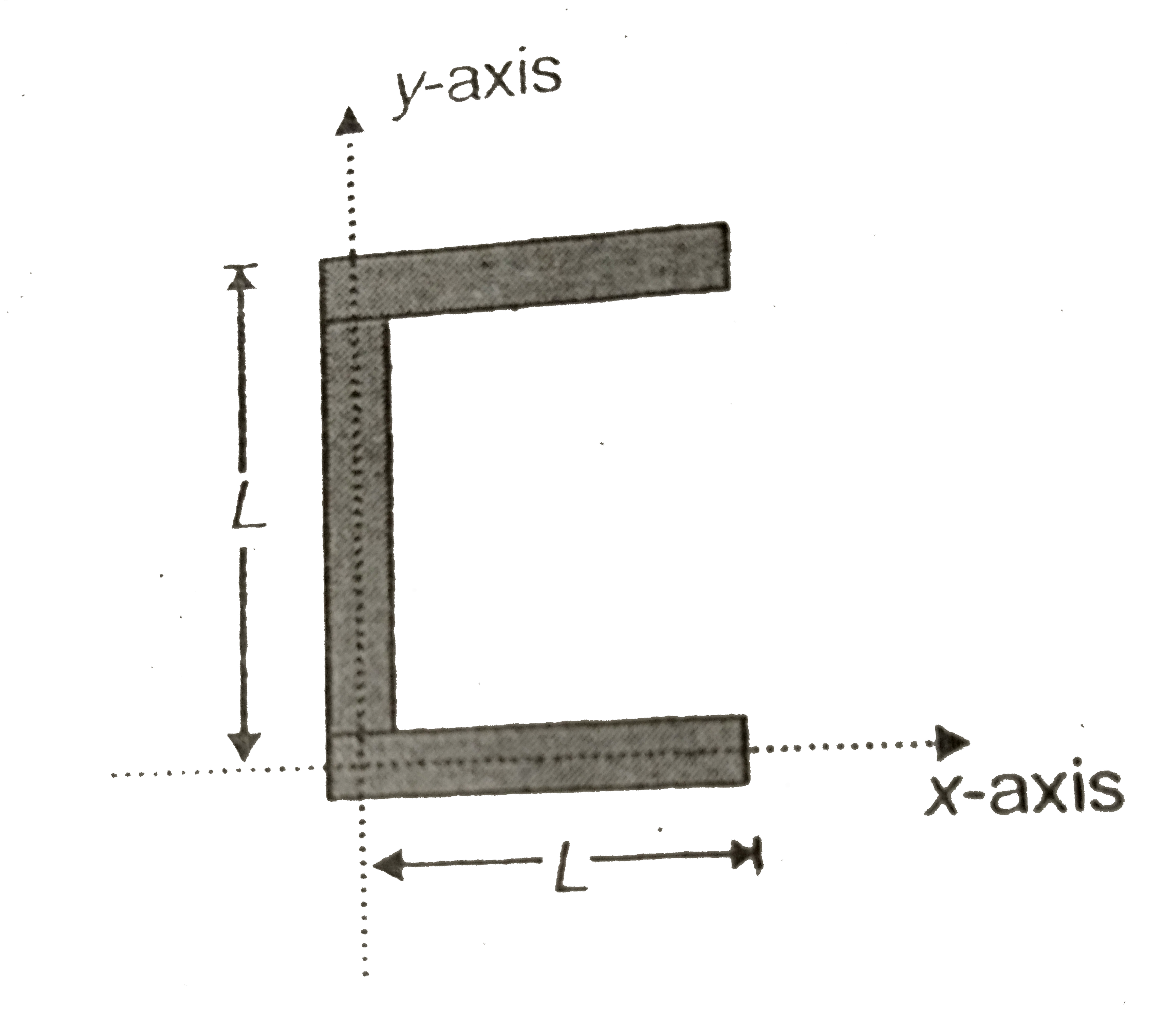
View SolutionLocate the centre of mass of arrangement shown in figure. The three rods are identical in mass and length
View SolutionOne fourth length of a uniform rod of length 2l and mass m is place don a horizontal table and the rod is held horizontal. The rod is released from rest. Find the normal reaction on the rod as soon as the rod is released.

View Solution
