The force acting on a particle of mass m moving along the x-axis is given by F(x)=Ax2−Bx.
Which one of the following is the potential energy of the particle?
2 Ax-B
−x26(2Ax−B)
Ax3−Bx2
Zero
The correct Answer is:B
Potential energy =−∫F(x)dx
U(x)=−∫(Ax2−BX)dx
U(x)=−Ax33+Bx22
U(x)=−x2/6(2Ax−3B)
Topper's Solved these Questions
Similar Questions
The potential energy of a particle of mass 2kg moving along the x-axis is given by U(x)=4x2−2x3( where U is in joules and x is in meters). The kinetic energy of the particle is maximum at
View SolutionThe potential energy of a particle of mass 1 kg free to move along x-axis is given by U(x)=(x22−x) joule. If total mechanical energy of the particle is 2J then find the maximum speed of the particle. (Assuming only conservative force acts on particle)
View Solution
Knowledge Check
A particle which is constant to move along the x−aξs , is subjected to a force in the same direction which varies with the distance x of the particle from the origin as F(x)=−Kx+ax3 . Hero K and a are positive constant . For x≥0, the fanctional from of the patential every U(x) of the particle is
A B
B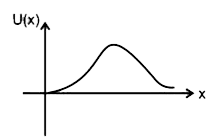 C
C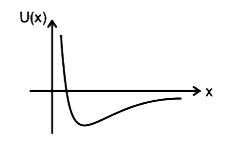 D
D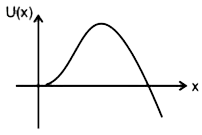
The potential energy of a particle of mass 1 kg moving along x-axis given by U(x)=[x22−x]J. If total mechanical speed (in m/s):-
A√5B√7C√3DNonePotential energy of a particle at position x is given by U=x2−5x. Which of the following is equilibrium position of the particle?
Ax=0Bx=5Cx=2.5Dx=7.5
The potential energy of a 2kg particle free to move along the x− axis is given by
V(x)[x44−x22]joule
The total mechanical energy of the particle is 0.75J. The maximum speed of the particle (in m/s) is :
View SolutionThe potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionThe velocity (v) of a particle of mass m moving along x-axis is given by v=α√x, where α is a constant. Find work done by force acting on particle during its motion from x=0 to x=2m :-
View SolutionThe displacement of a particle moving along x-axis is given by :
x=a+bt+ct2
The acceleration of the particle is.
View SolutionThe potential energy U(x) of a particle moving along x−axis is shown in figure. Which one of the following graphs represents the variation of kinetic energy of this particel if its total mechanical enery is E0

View Solution
