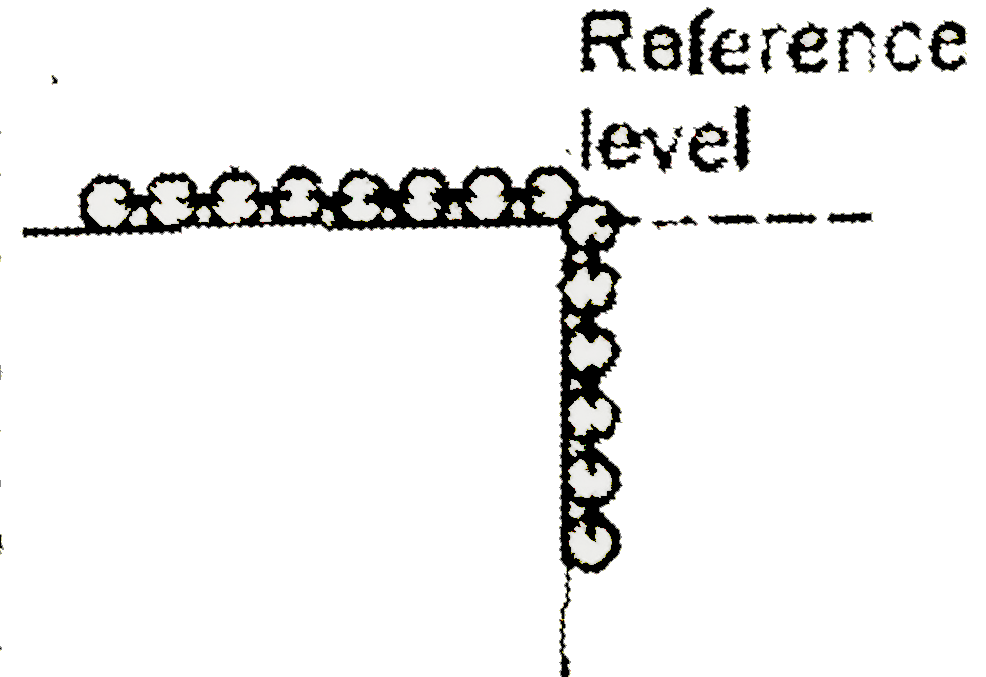
AS chain of length l and mass m lies o the surface of a smooth sphere of radius $R > l$ with one end tied to the top of the sphere. a.Find the gravitational potential energy of the chain with reference level at the centre of the sphere. B. suppose the chin is released and slides down the sphere. Find the kinetic eneergy of the chain, when it has slid through an angle $θ$ c. find the tangential acceleration $\frac{d v}{d t}$ of the chain when the chain starts sliding down.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C

(a) Mass per unit length length $= \frac{m}{l}$

$d m = \frac{m}{l} R d α$
$h = R \cos α$
$d U = (d m) g h = \frac{m g R^{2}}{l} \cos α . D α$
$∴ U = \int_{0}^{l / R} d U = \frac{m g R^{2}}{l} \sin (\frac{l}{R})$
(b) $K E = U_{i} - U_{f}$
Here, $U_{i} = \frac{m g R^{2}}{l} \sin (\frac{l}{R})$
and
$U_{f} = \int_{0}^{l / R + θ} d U = \frac{m g R^{2}}{l} [\sin (\frac{1}{R} + θ) - \sin θ]$
$∴ K E = \frac{m g R^{2}}{l} [\sin (\frac{l}{R}) + \sin θ - \sin (t h e t + \frac{a_{l}}{R})]$
(c ) $\frac{1}{2} m v^{2} = \frac{m g R^{2}}{l} = [\sin (\frac{l}{R}) + \sin θ - \sin (\frac{θ_{l}}{R})]$
or $v = \sqrt{\frac{2 g R^{2}}{l} [\sin (\frac{l}{R}) + \sin θ - \sin (θ + \frac{l}{R})]}$
$v^{2} = \frac{2 g R^{2}}{l} [\sin (\frac{l}{R}) + \sin θ - \sin (θ + \frac{l}{R})]$
$∴ 2 v . \frac{d v}{d t} = \frac{\frac{2 g R^{2}}{l} [\cos θ - \cos (θ + \frac{l}{R})]}{2 v} \frac{d θ}{d t}$ ....(i)
Here $\frac{\frac{d θ}{d t}}{v} = \frac{ω}{v} = \frac{l}{R}$
Substituting in Eq. (i), we get
$\frac{d v}{d t} = \frac{g R}{l} [1 - \cos (\frac{l}{R})]$ .

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A chain of length $l = π R / 4$ is placed. On a smooth hemispherical surface of radius $R$ with one of its ends fixed at the top of the sphere. Mass of chain is $\sqrt{π k g}$ and $R = 1 m . (g = 10 m / s^{2})$ .
The gravitational potential energy of the chain considering reference level at the base of hemisphere is
A20 J
B $20 \sqrt{2} J$
C40 J
D $40 \sqrt{2} J$
Question 2 - Select One
A chain of length $l = π R / 4$ is placed. On a smooth hemispherical surface of radius $R$ with one of its ends fixed at the top of the sphere. Mass of chain is $\sqrt{π k g}$ and $R = 1 m . (g = 10 m / s^{2})$ .
If the chain sliped down the sphere, kinetic energy of the chain when it has sliped through an angle $θ = \frac{π}{4}$ .
A $23.4 J$
B $63.44 J$
C80 J
D $97.4 J$
Question 3 - Select One
Two spheres each of mass $M$ and radius $R$ are separated by a distance of $r$ . The gravitational potential at the midpoint of the line joining the centres of the spheres is
A $- \frac{G M}{r}$
B $- \frac{2 G m}{r}$
C $- \frac{G M}{2 r}$
D $- \frac{4 G M}{r}$

DC PANDEY-WORK, ENERGY & POWER-Level 2 Subjective

Home
Ask Doubt
Profile