A rough horizontal plate rotates with angular velocity ω about a fixed verticle axis. A particle or mass m lies on the plate at a distance 5a4 from this axis. The coefficient of friction between the plate and the particle is 13 . The largest value of ω2 for which the oparticle will continue to be at rest on the revolving plate is
g3a
4g5a
4g9a
4g15a
The correct Answer is:D
μmg=nRω2
:. ω2=μgR=(1/3)g5a/4=4g15a
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Subjective
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A rough horizontal plate rotates with a constant angular velocity w about its vertical axis. A particle of mass m lies on the plate at a distance 5a4 from the axes. If the coefficient of friction is 13 and the particle remains at rest relative to the plane, show that w≤√4g15a. The particle is now connected to axis by a horizontal elastic string, of natural length a and modulus 3 mg. If the particle remains at rest relative to the plate and at a distance 5a4, show that the greatest possible angular velocity is √1315.ga and find the least possible velocity.
View SolutionA particle of mass m is placed over a horizontal circular table rotating with an angular velocity ω about a vertical axis passing through its centre. The distance of the object from the axis is r. Find the force of friction f between the particle and the table.
View Solution
Knowledge Check
A uniform rod of mass m and length l rotates in a horizontal plane with an angular velocity ω about a vertical axis passing through one end. The tension in the rod at a distance x from the axis is
A12mω2xB12mω2(1−x2l)C12mω2l(1−x2l2)D12mω2l[1−xl]A rigid body of mass m rotates with angular velocity ω about an axis at a distance a from the centre of mass G. The radius of gyration about a parallel axis through G is k. The kinetic energy of rotation of the body is
A12mk2ω2B12ma2ω2C12m(a2+k2)ω2D12m(a+k)2ω2A ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
Aω0μR2gBω0g2μRC2ω0RμgDω0R2μg
Find the mass of a mole of colloid particles if during their centrifuging with an angular velocity ω about a vertical axis the concentration of the particles at the distance r2 from the rotation axis is η times greater than that at the distance r1 (in the same horizontal plane). The densities of the particles and the solvent are equal to ρ and to ρ0 respectively.
View SolutionA circular plate is rotating about its own axis at an angular velocity 100 revolutions per minute. The linear velocity of a particle P of plate at a distance 4.2cm from axis of rotation is
View SolutionA block is resting on a horizontal plate in the xy plane and the coefficient of friction between block and plate is μ. The plate begins to move with velocity v=bt2 in x direction At what time will the block start sliding on the plate?
View SolutionA circular of radius 20 cm is rotating about its own axis at an angular velocity ω . The angular velocity of a particle 'A' which is at a distance 10 cm from the axis of rotation is
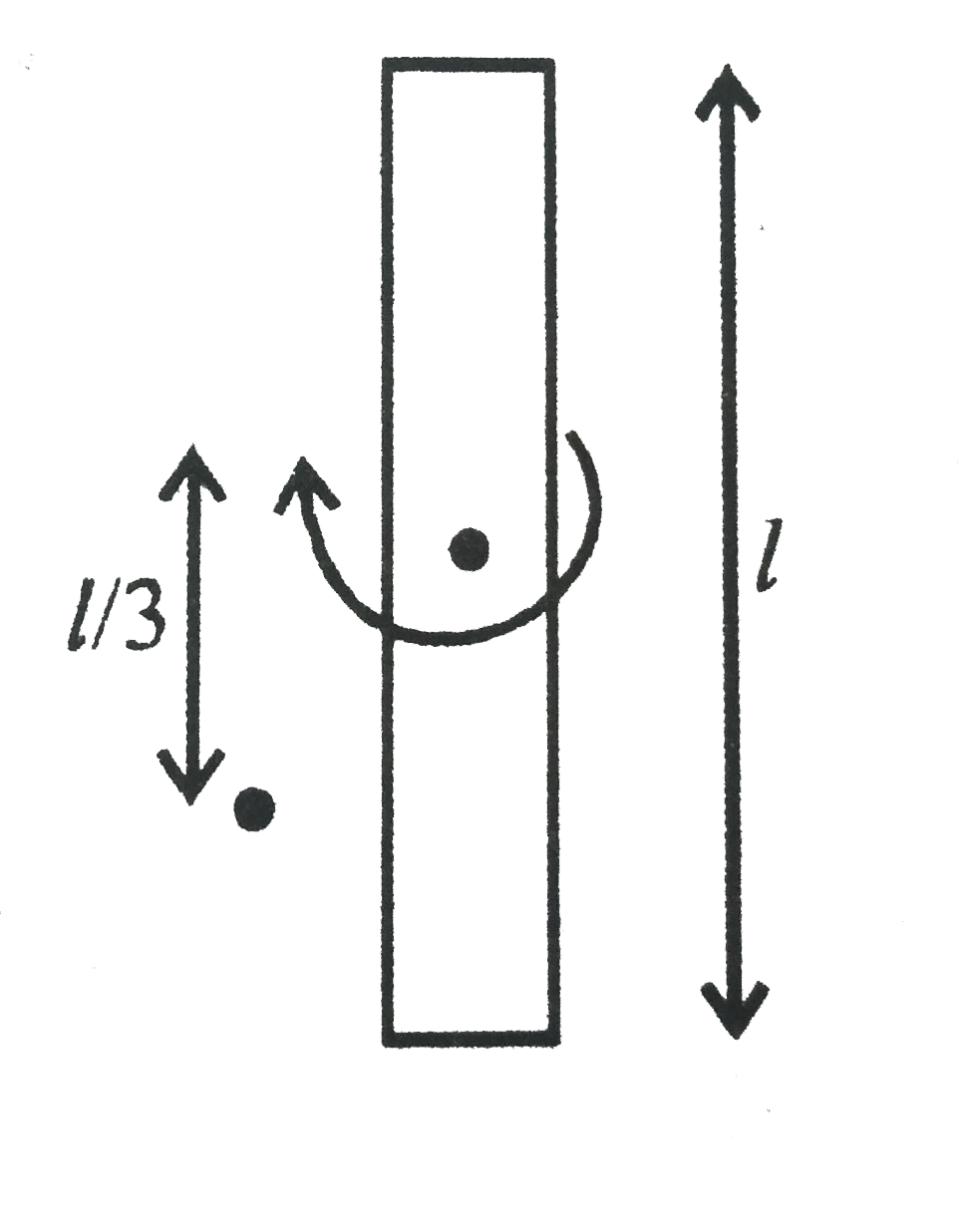
View SolutionA uniform rod of length l and mass M rotating about a fixed vertical axis on a smooth horizontal table. It elastically strikes a particle placed at a distance l/3 from its axis and stops. Mass of the particle is -
 .
.
View Solution