A dics is rotating in a room. A boy standing near the rim of the disc of radius R finds the water droplet falling from the ceiling is always falling on his head. As one drop hits his head, other one starts from the ceiling. If height of the roof above his head is H , then angular velocity of the disc is
π√2gRH2
π√2gHR2
π√2gH
None of these
The correct Answer is:C
t=T
:. √2Hg=2πω
ω=2π√g2H=π√2gH
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 More Than One Correct5videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 2 Comprehension Based5videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Level 1 Subjective13videos
CIRCULAR MOTION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct27videos
COMMUNICATION SYSTEM
Similar Questions
In the figure (i) a disc of mass M(kg) and radius R(m) is rotating smoothly about a fixed vertical axis AB with angular speed 26rad/s A rod rod CD of length R2(m) and mass M(kg) is hinged at one end at point 'D' on the disc. The rod remains in vertical position and rotates along with the disc about axis AB. At some moment the rod CD gets a very smal impulse at point 'C' due to air due to which the rod falls on the disc along one radius and sticks to the disc as shown in figure (ii). Now find the angular velocity of the disc in rad/s.
View SolutionWater drops are falling from a tip at regular time intervals. When the fifth drop is near to fall from tap the first drop is at ground. If the top is fixed at height H from ground then find out
(i) the height of the second drop from ground
(ii) distance between the second and third drop
(iii) velocity of third dropView Solution
Knowledge Check
- Question 1 - Select One
A boy watches a jet plane flying from north to south. When the jet is just seen above his head, the sound of jet appears to reach him makin some angle with horizontal from north.If the velocity of jet is v/2, then find the angle.
A60∘B30∘C45∘D15∘ - Question 2 - Select One
Two rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
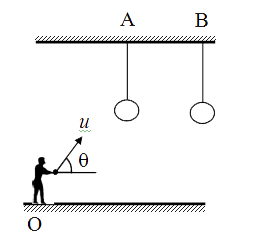
The maximum height attained by the ball above the floor is:A2.2 mB1.8 mC2.6 mDNone of these - Question 3 - Select One
Two rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
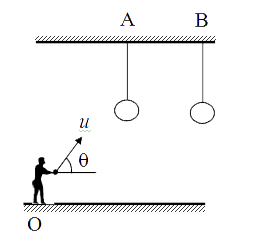
The projection speed of the ball is:A3 m/sB4 m/sC5 m/sD2.5 m/s
A man of height h0=2m is bungee jumping from a platform situated at a height h = 25 m above a lake One end of an elastic rope is attached to his foot and the other end is fixed to the platform He starts falling from rest in vertical position. The length and elastic properties of the rope are chosen so that his speed will have been reduced to zero at instant when his head reaches the surface of water. Ultimetely the jumper is hanging from the rope with his head 8m above the water. Find the maxima acceleration acheived during the jump in m/s2)
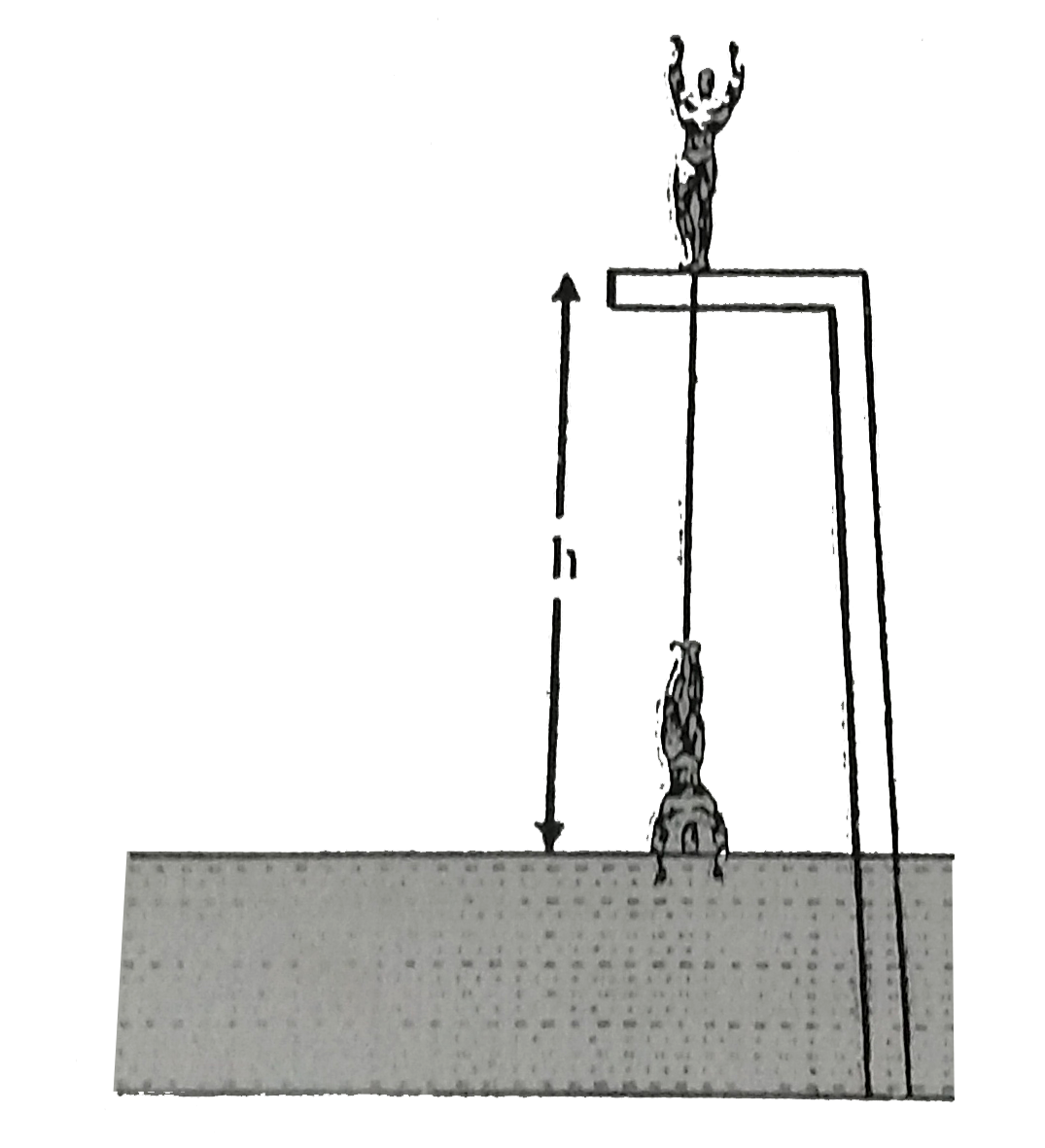View SolutionIn the Figure FE is a man of height H standing on a floor. E is eye of the man and F is his foot. The distance between eye and the head is negligible. A steel ball of radius r is suspended in front of him. The distance of the ball from the man is H and height of the centre of the ball from the floor is H2. It is given that r<<H. The surface of the ball acts like a mirror and the man sees his image in it. Calculate the angle subtended by the image at the eye of the man.
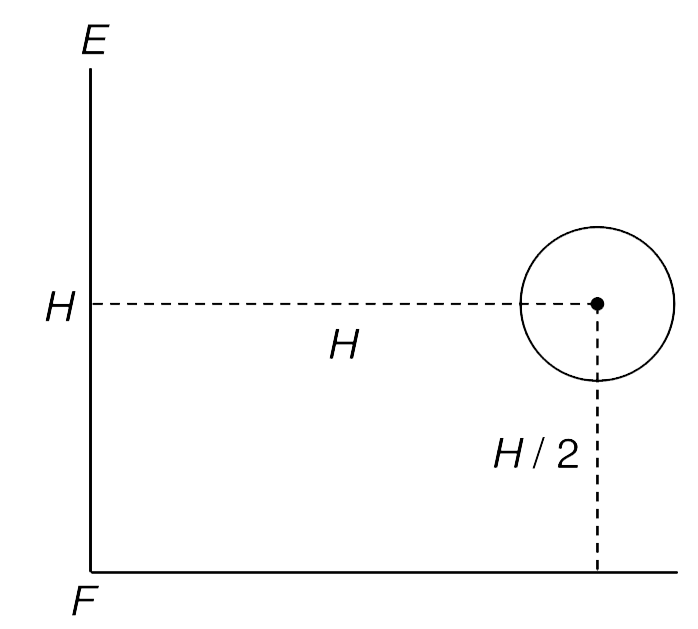View Solution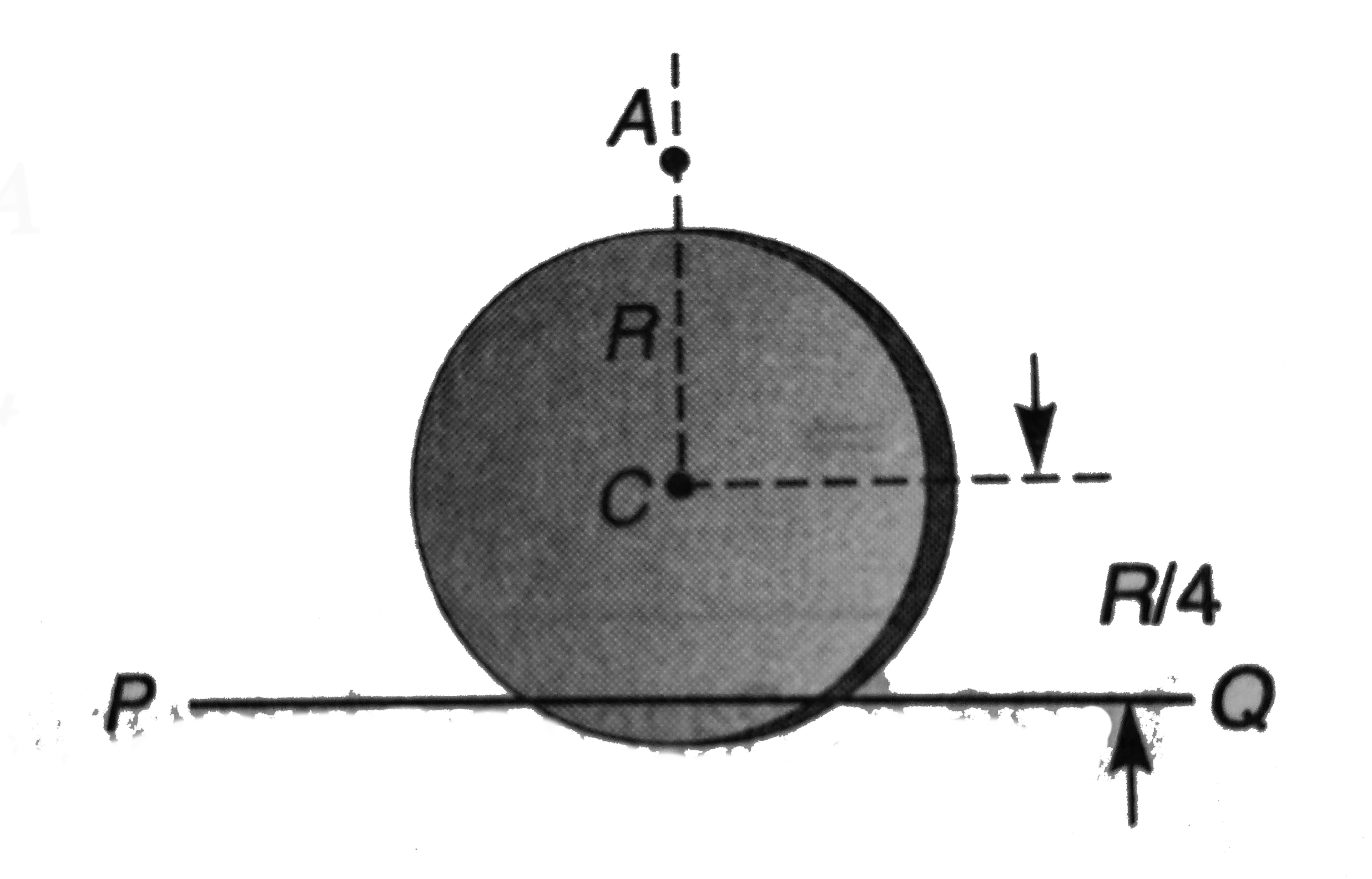
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.View Solution-
A uniform circular disc has radius R and mass m. A particle, also of mass m, if fixed at a point A on the edge of the disc as shown in the figure. The disc can rotate freely about a horizontal chord PQ that is at a distance R/4 from the centre C of the disc. The line AC is perpendicular to PQ. Initially the disc is held vertical with the point A at its highest position. it is then allowed to fall, so that it starts rotation about PQ. Find the linear speed of the particle as it reaches its lowest position.View Solution A box B of mass M hangs from an ideal spring of force constant k. A small particle, also of mass M, is stuck to the ceiling of the box and the system is in equilibrium. The particle gets detached from the ceiling and falls to strike the floor of the box. It takes time t for the particle to hit the floor after it gets detached from the ceiling. The particle, on hitting the floor, sticks to it and the system thereafter oscillates with a time period T. Find the height H of the box if it is given that t=T6√2. Assume that the floor and ceiling of the box always remian horizontal.
View Solution