A projectile of mass 3m is projected from ground with velocity at . At highest point it explodes into two pieces. One of mass 2m and the other of mass m. Both the pieces fly off horizontally in opposite directions. Mass 2m falls at a distance of from point of projection. Find the distance of second mass from point of projection where it strikes the ground.
The correct Answer is:C, D
Range of the projectile in the absence of explosion
The path of centre of mass of projectile will not change, i.e. is still 80 m. Now, from the definition of centre of mass
or
Solving this equation, we get
Therefore, the mass m will fall at a distance from point of projection.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples13videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 11videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
A particle is projected from ground with velocity 20(√2)m/s at 45∘. At what time particle is at height 15 m from ground? (g=10m/s2)
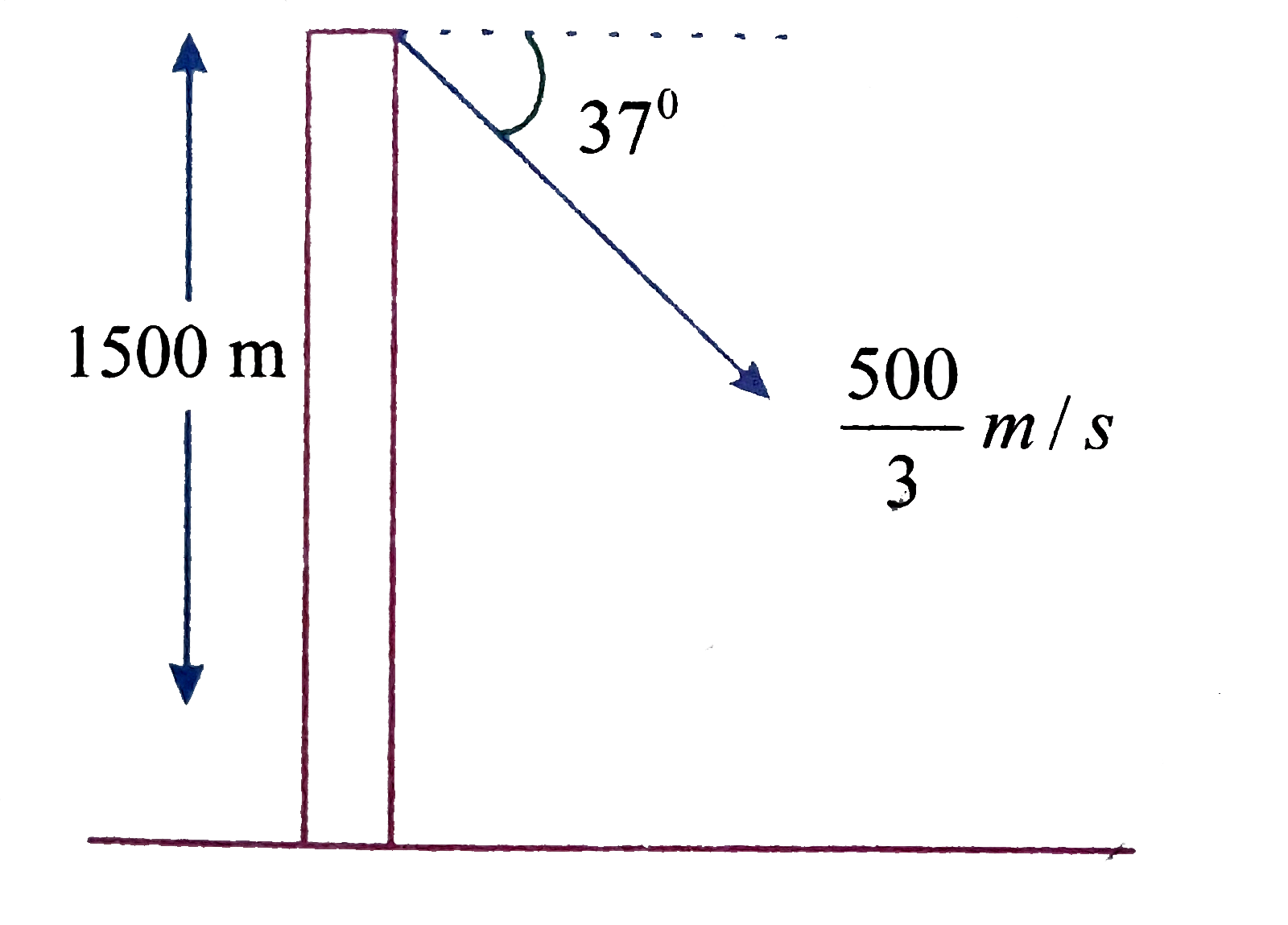
View SolutionA particle is projected from a tower as shown in figure, then find the distance from the foot of the tower where it will strike the ground. (g=10m/s2)
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One or More
A particle is projected from ground with velocity 40√2m/s at 45∘. At time t=2s
Adisplacement of particle is 100mBvertical component of velocity is 20m/sCvelocity makes an angle tan−1(2) with verticalDparticle is at height of 60m from ground - Question 2 - Select One
A particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
A3R4B3R2C5R4D3R - Question 3 - Select One
A particle of mass 4m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 3m, respectively, such that the smaller mass comes to rest. The larger mass finally falls at a distance x from the point of projection, where x is equal to
A2R3B7R6C5R4Dnone of these
A particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
View SolutionThe particle of mass 1 kg is projected with velocity 20√2m/s at 45∘ with ground . When , the particle is at highest point (g=10m/s2),
 View Solution
View SolutionA ball is projected from a point O as shown in figure. It will strike the ground after (g = 10 m/s2)
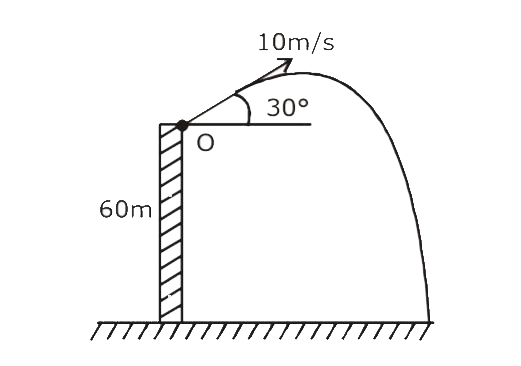 View Solution
View SolutionA ball is projected from a point O as shown in figure it will strike the ground after (g = 10 m/s2 )
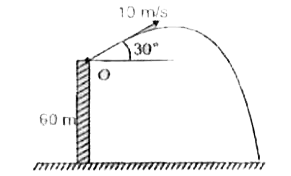 View Solution
View SolutionA particle of mass 'm' is projected from ground with velocity u making angle θ with the vertical. The de-Broglie wave length of the particle at the highest point is:
View Solution

