A particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
43R
32R
54R
2.5R
To solve the problem, we will analyze the motion of the particle and apply the concept of the center of mass.
1. Understanding the Initial Conditions:
- A particle of mass 3m is projected from the ground at an angle, reaching a horizontal range R.
- At the highest point of its trajectory, it breaks into two pieces: one of mass m and the other of mass 2m.
2. Analyzing the Highest Point:
- At the highest point, the horizontal distance covered by the particle is R/2 (since the total range is R and the highest point is halfway in the horizontal direction).
- The smaller mass m comes to rest immediately after the break.
3. Position of the Masses After Breaking:
- The mass m will fall straight down from the highest point, which is at a horizontal distance of R/2.
- The larger mass 2m will continue to move horizontally and will fall at a distance x from the point of projection.
4. Using the Center of Mass Concept:
- The center of mass of the system before the break is at the point where the total mass is 3m and is located at R (the range).
- After the break, the center of mass must remain in the same horizontal position (since no external horizontal forces act on the system).
5. Setting Up the Equation for Center of Mass:
- The center of mass Xcm can be expressed as:
Xcm=m⋅R2+2m⋅xm+2m
- Since the center of mass remains at R, we set up the equation:
R=m⋅R2+2m⋅x3m
6. Simplifying the Equation:
- Multiply both sides by 3m:
3mR=m⋅R2+2m⋅x
- Dividing through by m:
3R=R2+2x
7. Rearranging the Equation:
- Rearranging gives:
2x=3R−R2
- Converting 3R to a common denominator:
2x=6R2−R2=5R2
- Dividing by 2:
x=5R4
Final Answer:
The distance x from the point of projection where the larger mass lands is:
x=5R4
- A particle of mass 3m is projected from the ground at an angle, reaching a horizontal range R.
- At the highest point of its trajectory, it breaks into two pieces: one of mass m and the other of mass 2m.
- At the highest point, the horizontal distance covered by the particle is R/2 (since the total range is R and the highest point is halfway in the horizontal direction).
- The smaller mass m comes to rest immediately after the break.
- The mass m will fall straight down from the highest point, which is at a horizontal distance of R/2.
- The larger mass 2m will continue to move horizontally and will fall at a distance x from the point of projection.
- The center of mass of the system before the break is at the point where the total mass is 3m and is located at R (the range).
- After the break, the center of mass must remain in the same horizontal position (since no external horizontal forces act on the system).
- The center of mass Xcm can be expressed as:
Xcm=m⋅R2+2m⋅xm+2m
- Since the center of mass remains at R, we set up the equation:
R=m⋅R2+2m⋅x3m
- Multiply both sides by 3m:
3mR=m⋅R2+2m⋅x
- Dividing through by m:
3R=R2+2x
- Rearranging gives:
2x=3R−R2
- Converting 3R to a common denominator:
2x=6R2−R2=5R2
- Dividing by 2:
x=5R4
The distance x from the point of projection where the larger mass lands is:
x=5R4
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - More a than one option is Correct1videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery27videos
CENTRE OF MASS
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective21videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
Similar Questions
A projectile of mass 3m is projected from ground with velocity 20√2m/s at 45∘. At highest point it explodes into two pieces. One of mass 2m and the other of mass m. Both the pieces fly off horizontally in opposite directions. Mass 2m falls at a distance of 100m from point of projection. Find the distance of second mass from point of projection where it strikes the ground.
(g=10m/s2)View SolutionIf a particle of mass m is thrown with speed at an angle 60° with horizontal, then angular momentum of particle at highest point about point of projection is
View Solution
Knowledge Check
- Question 1 - Select One
A particle of mass 4m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 3m, respectively, such that the smaller mass comes to rest. The larger mass finally falls at a distance x from the point of projection, where x is equal to
A2R3B7R6C5R4Dnone of these - Question 2 - Select One
A particle of mass 3m is projected from the ground at some angle with horizontal. Its horizontal range is R. At the highest point of its path it breaks into two pieces of masses m and 2m respectively. The smallar mass comes to rest. The larger mass finally falls at a distance x from the point of projection where x is equal to
A3R4B3R2C5R4D3R - Question 3 - Select One
A particle is projected from the ground with a kinetic energy E at an angle of 60° with the horizontal. Its kinetic energy at the highest point of its motion will be
AE/√2BE/2CE/4DE/8
In figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
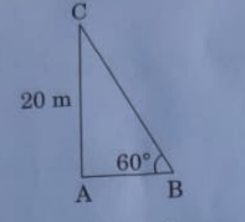 View Solution
View SolutionA particle of mass m is projected with a velocity μ at an angle of θ with horizontal.The angular momentum of the particle about the highest point of its trajectory is equal to :
View SolutionA particle is projected such that its horizontal range would be R. At the highest point, the particle breaks into two identical parts P and Q. If P comes to rest, the horizontal distance of point from the point of projection (i.e. origin) where the particle Q lands on the ground is
View SolutionA particle of mass m is projected at an angle α to the horizontal with an initial velocity u. The work done by gravity during the time it reaches its highest point is
View SolutionA particle of mass m is projected at an angle with horizontal with kinetic energy E. the potential energy at the top of its trajectory is E2. Find the range.
View Solution

