After a completely inelastic collision two objects of the same mass and same initial speed are found to move away together at half their initial speed. Find the angle between the initial velocities of the objects.
120∘
90∘
180∘
60∘
The correct Answer is:A
Let θ be the desired angle. Linear momentum of the system will remain conserved.
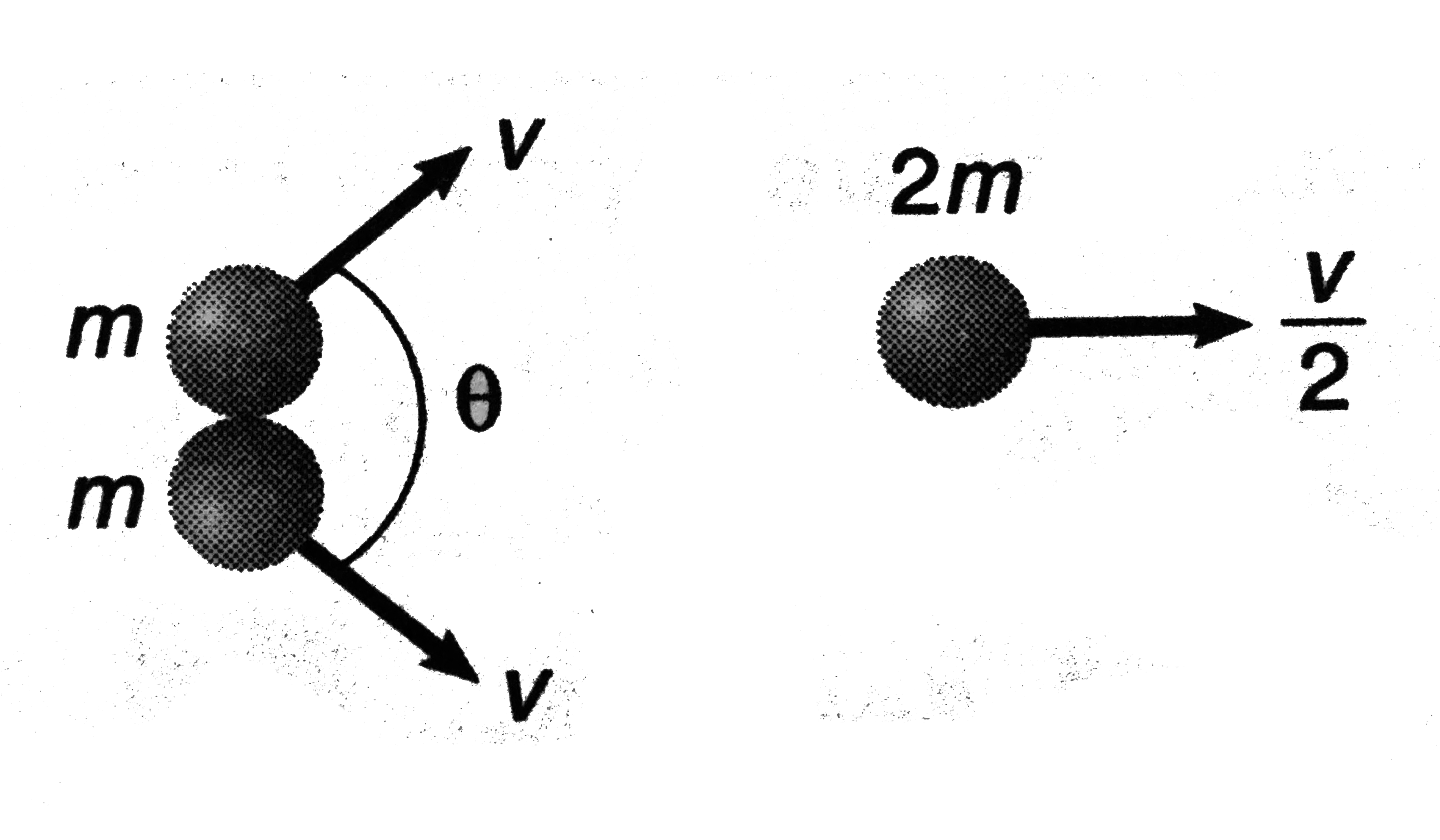
Hence, p2=p21+p22+2p2p2cosθ
or {2m(v2)}2=(mv)2+(mv)2+2(mv)(mv)cosθ
or 1=1+1+2cosθ or cosθ=−12
∴θ=120∘
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples13videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 11videos
CENTRE OF MASS, LINEAR MOMENTUM AND COLLISION
- BOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions15videos
CENTRE OF MASS, IMPULSE AND MOMENTUM
- BOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery19videos
CIRCULAR MOTION
Similar Questions
Consider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
View SolutionAn object A of mass 2 kg is moving on a frictionless horizontal track has perfectly inelastic collision with another object B of mass 3 kg made of the same material and moving in front of A in same direction their common speed after the collision is 4m/s Due to the collision the temperature of the two objects which was initially the same, is increased though only by 0.006∘ C What was the initial speed (∈m/s) of the colliding object A before the collision?
View Solution
Knowledge Check
- Question 1 - Select One
After a totally inelastic collision, two objects of the same mass and same initial speeds are found to move together at half of their initial speeds. The angle between the initial velocities of the objects is
A30∘B60∘C45∘D37∘ - Question 2 - Select One
A ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass m but at rest. After the collision if the two balls move with the same speeds , the angle between their directions of motion will be:
A30∘B60∘C120∘D90∘ - Question 3 - Select One
A particle of mass m is projected from the ground with an initial speed u0 at an angle α with the horizontal. At the highest point of its trajectory, it makes a completely inelastic collision with another identical particle, which was thrown vertically upward from the ground with the same initial speed u0. The angle that the composite system makes with the horizontal immediately after the collision is
Aπ4Bπ4+αCπ4−αDπ2
A sphere has a elastic obique collision with another identical sphere which is initially at rest. The angle between their velocities after the collision is
View SolutionTwo stones are projected simultaneously from a tower a differenct angles of projection with same speed 'u'. The distance between two stones is increasing at constant rate 'u'. Then the angle between the initial velocity vectors of the two stones is :
View SolutionConsider the elastic collision f two bodies A and B of equal mass. Initially B is at rest and A moves with velocity v. After the collision -
View SolutionTwo particles of equal masses moving with same momentum collide perfectly in-elastically. After the collision the combined mass moves with half of the speed of the individual masses. The angle between the initial momenta of individual particle is
View SolutionIf momentum of two objects are of same magnitude. Then speed of lighter object will be
View Solution
