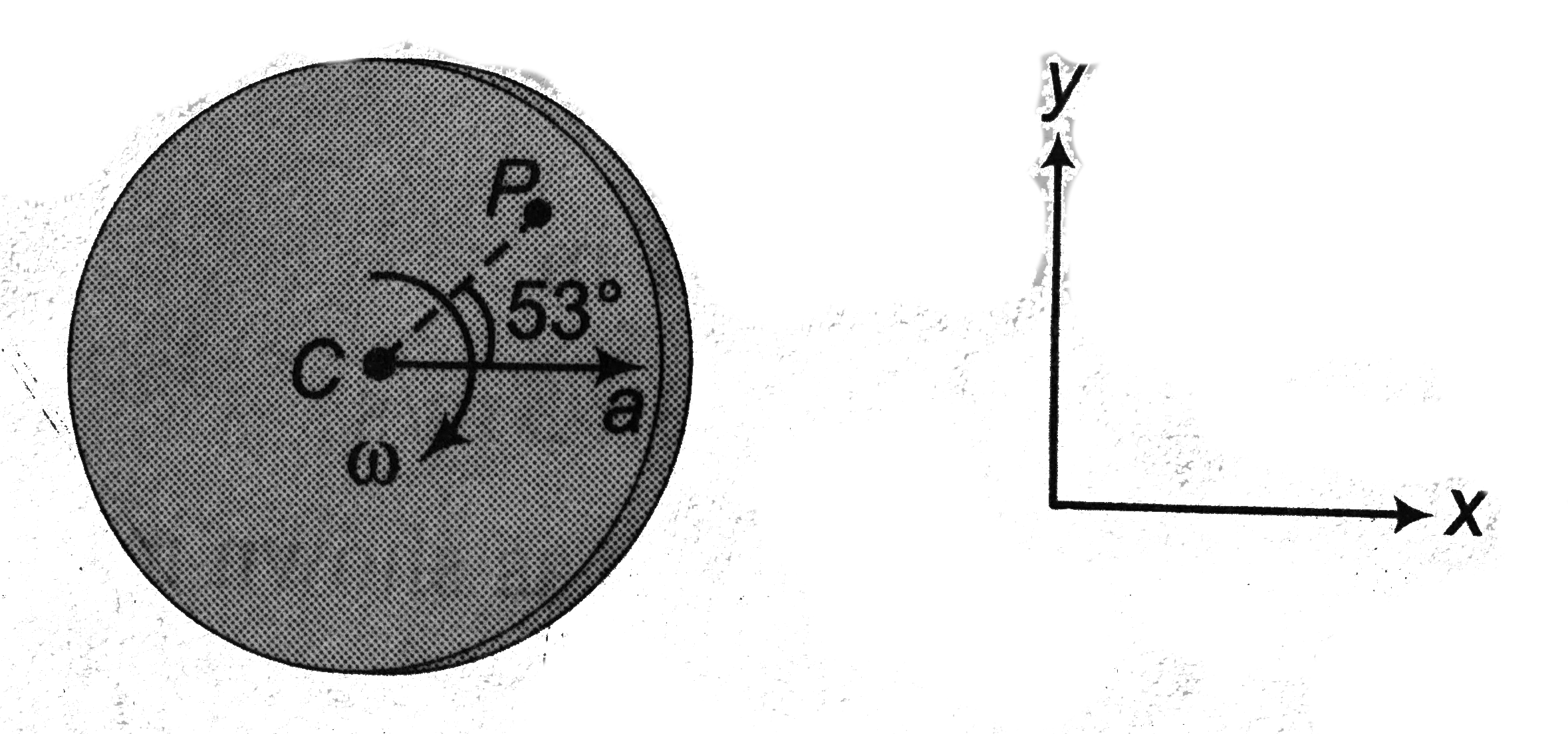
In the shown figure,
a=2m/s2,ω=(2t)rods−1 and CP=1m
In terms of ˆi and ˆj, find linear acceleration of the particle at P at P at t=1 s
 For particle at P
For particle at P
r=CP=1m
⇒α=dωdt=ddt(2t)=2rad/s2
At t=1 s
ω=2rad/s
α=2rad/s2
at=rα=2m/s2
ar=rω2=4m/s2
and a=2m/s2
Net acceleration of P is the vector sum of three terms a, ar and at as shown in figure below.
∴aP=2ˆi+(2cos37∘ˆi−2sin37∘ˆj)+(−4sin37∘ˆi−2sin37∘ˆj)−(−4sin37∘ˆi−4cos37∘ˆj)
=2ˆi+1.6ˆi−1.2ˆj−2.4ˆi−3.2ˆj
=(1.2ˆi−4.4ˆj)m/s2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Solved Examples
25 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Miscellaneous Examples
2 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Knowledge Check
If velcotiy of a particle is given by v=2t−1 then find the acceleration of particle at t = 2s.
A2B4C8D6the angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
A10rads2B5rads2CZeroD3rads2. If the velocity of a particle is (10 + 2 t 2) m/s , then the average acceleration of the particle between 2s and 5s is
A2m/s2B4m/s2C12m/s2D14m/s2
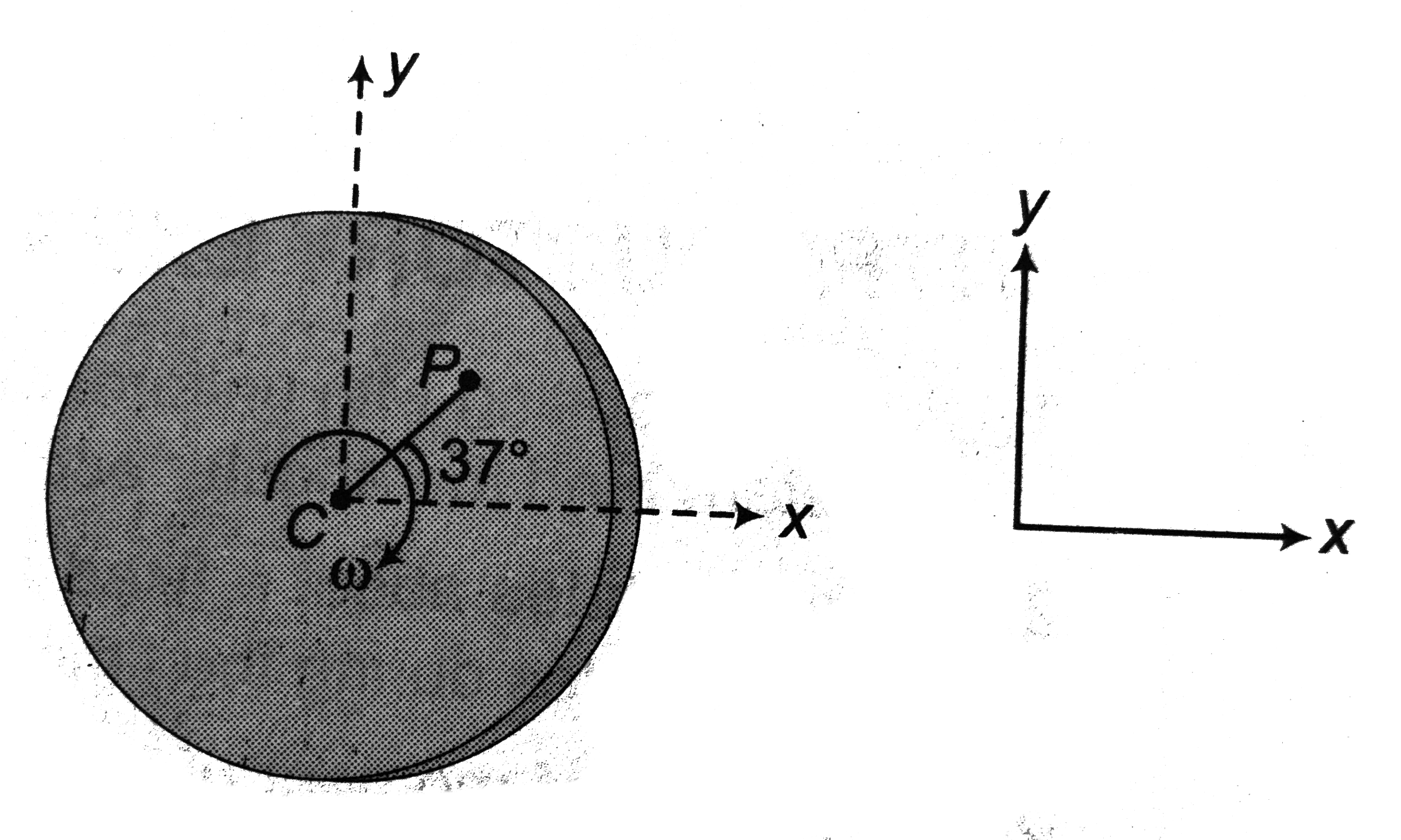
A circular disc is rotating with an angular speed (in radian per sec)
ω=2t2
given, CP=2m
In terms of ˆi,ˆj and ˆk at t=1s
find,
(a). ω
(b). α
(c). linear velocity of the particle lying at P (d). linear acceleration of the particle lying P
View SolutionIn the figure shown, find acceleration of the system and tenslons T1,T2andT3(Take=10m/s2)
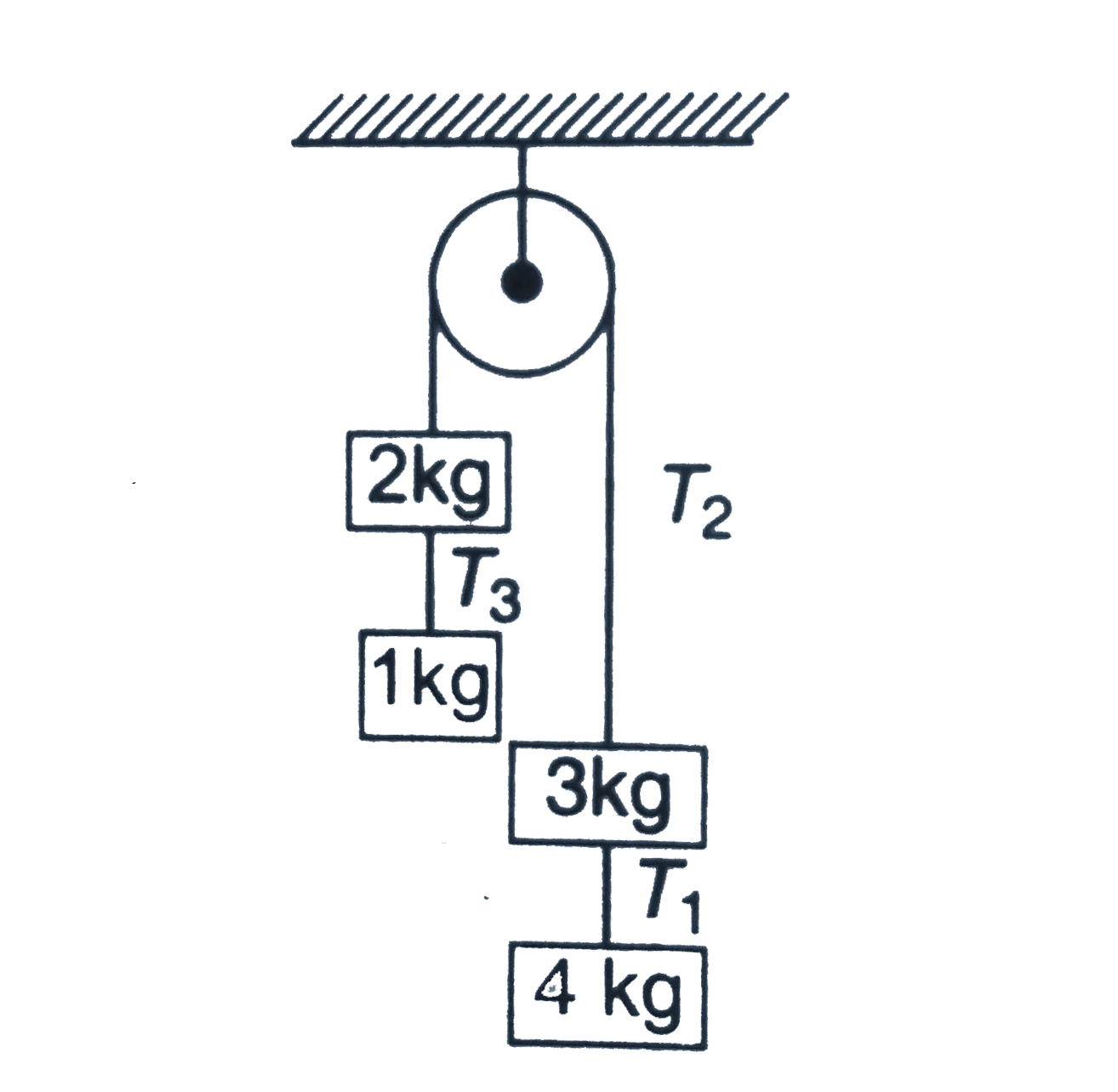
View SolutionVelocity of a particle in x-y plane at any time t is v=(2tˆi+3t2ˆj)m/s At t=0, particle starts from the co-ordinates (2m,4m). Find
(a) acceleration of the particle at t=1s.
(b) position vector and co-ordinates of the particle at t=2s.
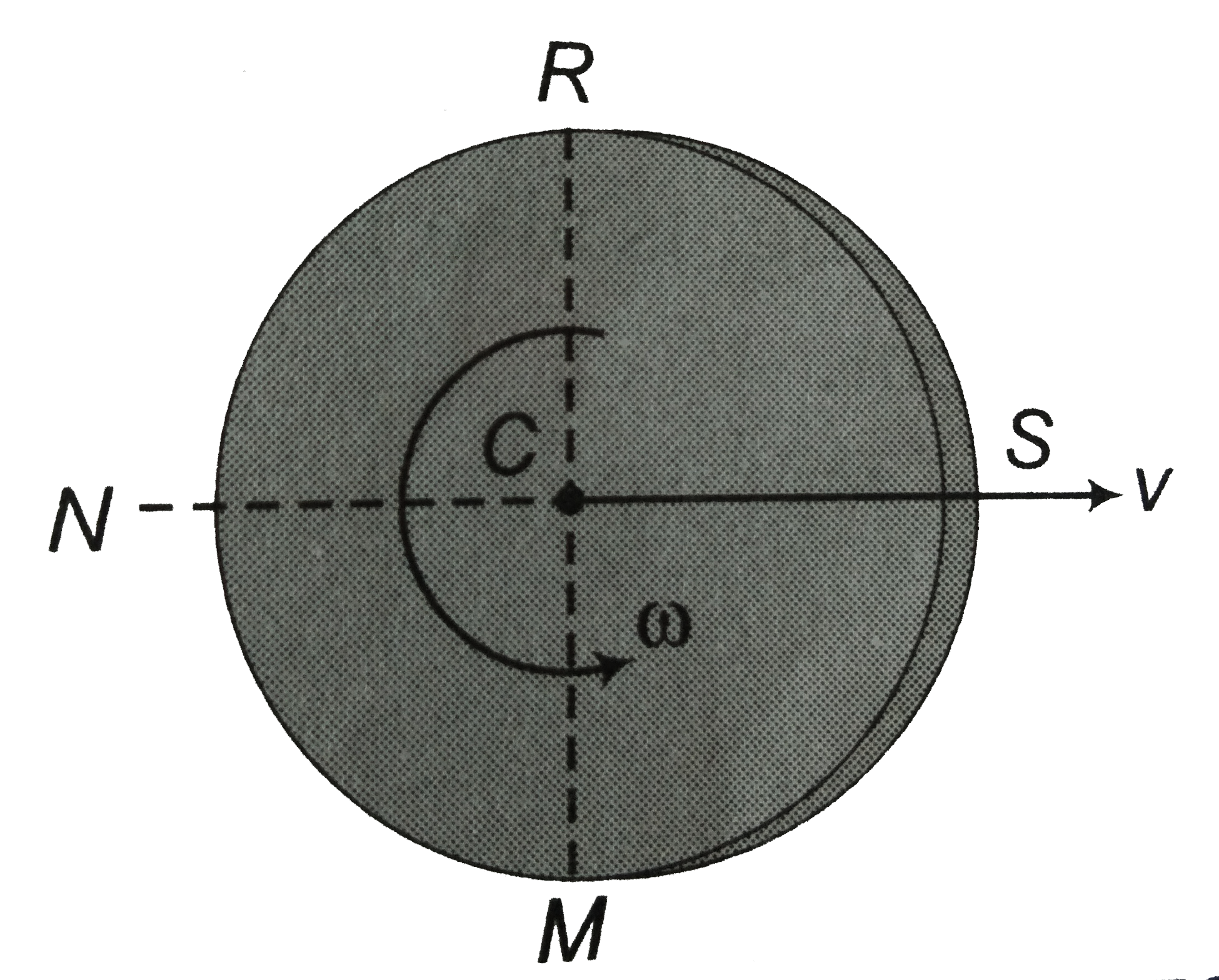
View SolutionIn the sae figure. If v and ω both are constant, then find linear acceleration of point M,N,R and S in terms of R,ω,ˆi and ˆj where R is the radius disc.
View SolutionIf the velocity of a particle is (10+2t^(2)m/s ,then the average acceleration of the particle between 2s and 5s is (in m/s^2)
View Solution