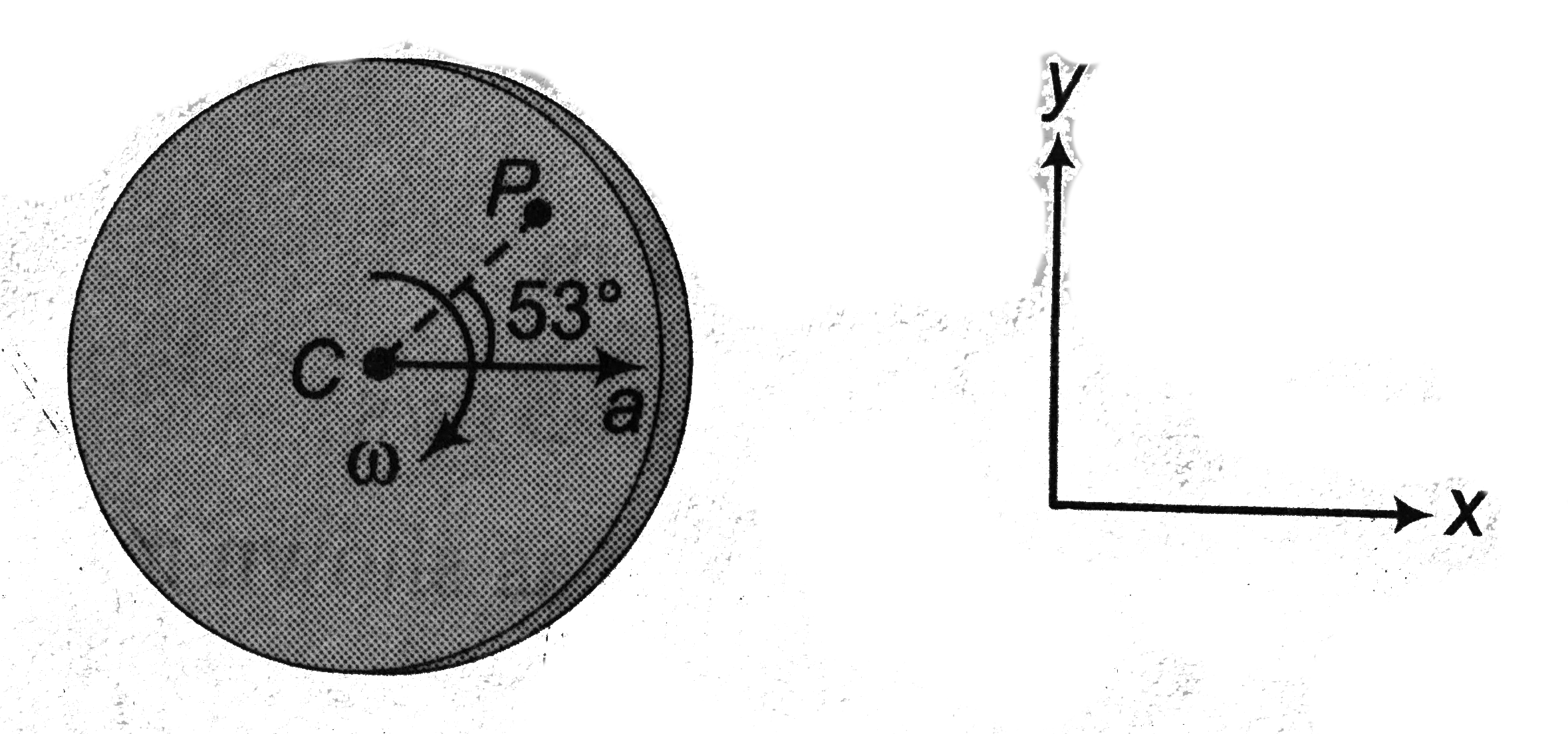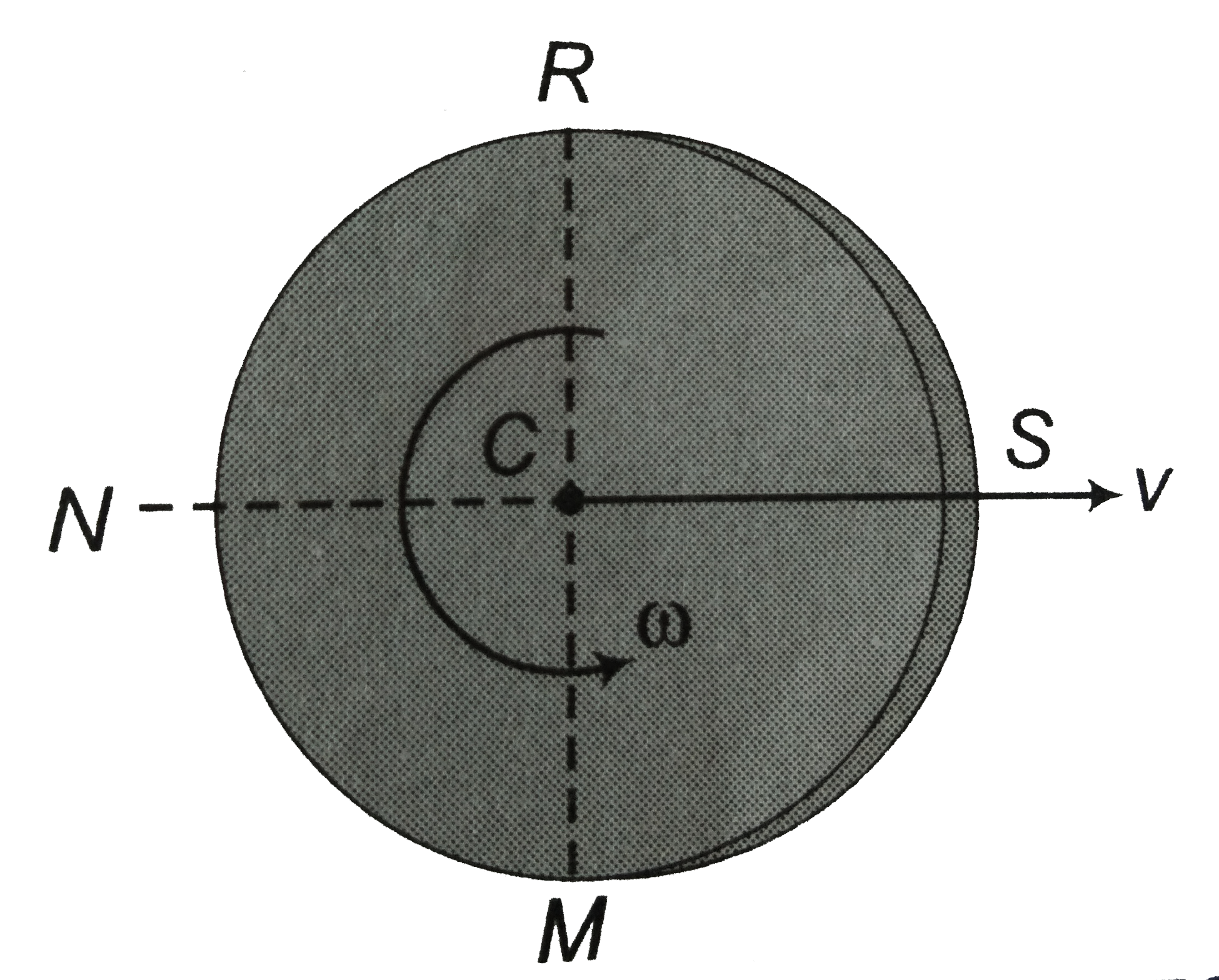
In the figure shown ω=v2R in terms of ˆi and ˆj find linear velocities of particles M, N, R and S.

ωR=v2
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.83videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.92videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.64videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
A disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in Fig. The magnitude of acceleration of point P as shown in the figure at an instant when its linear velocity is v and angular velocity is ω will be a
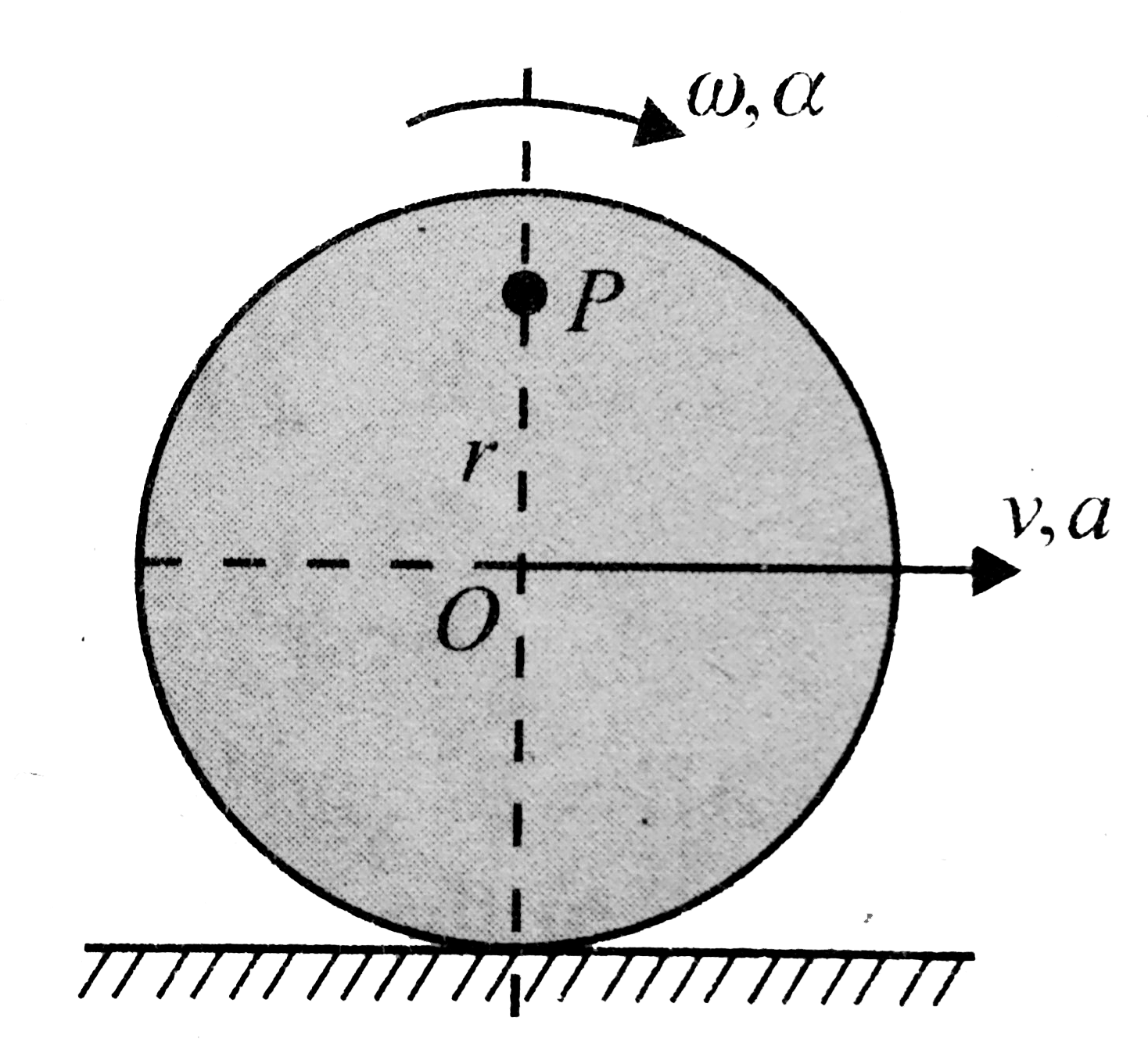 A√(a+rα)2+(rω2)2BarRC√r2α2+r2ω4Drα
A√(a+rα)2+(rω2)2BarRC√r2α2+r2ω4Drα
In the sae figure. If v and ω both are constant, then find linear acceleration of point M,N,R and S in terms of R,ω,ˆi and ˆj where R is the radius disc.
View Solution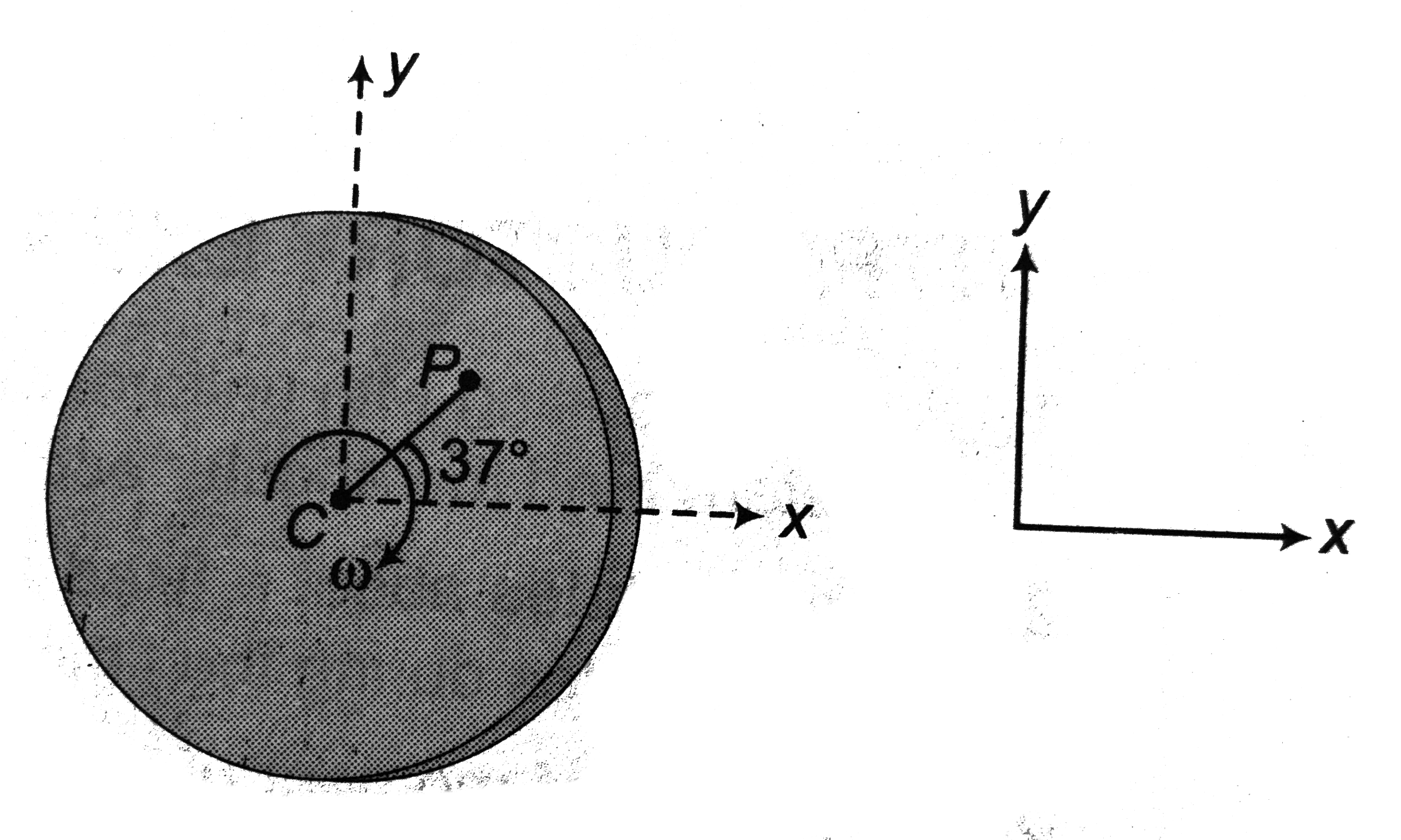
A circular disc is rotating with an angular speed (in radian per sec)
ω=2t2
given, CP=2m
In terms of ˆi,ˆj and ˆk at t=1s
find,
(a). ω
(b). α
(c). linear velocity of the particle lying at P (d). linear acceleration of the particle lying PView SolutionIf angular velocity of a particle having position vector →r=(2ˆi−2ˆj+2ˆk)m about the origin is →w=(2ˆi−2ˆj−ˆk)rads then magnitude of linear velocity of the particle will be
View SolutionA particle is given an initial velocity of →u=(3ˆi+4ˆj)m/s. Acceleration of the particle is →a=(3t2+2tˆj)m/s2. Find the velocity of particle at t=2s.
View Solutionif the displacement of the particle at an instant is given by
y=rsin(ωt−θ)
where r is amplitude of oscillation. ω is the angular velocity and −θ is the initial phase of the particle, then find the particle velocity and particle acceleration.View SolutionIf →ω=2ˆi−3ˆj+4ˆk and →r=2ˆi−3ˆj+2ˆk then the linear velocity is
View SolutionA charged particle enters a uniform magnetic field with velocity v0=4m/s perpendicular to it, the length of magnetic field is x=(√32)R, where R is the radius of the circular path of the particle in the field. Find the magnitude of charge in velocity (in m/s) of the particle when it comes out of the field.
View Solution