A body moves in a circular orbit of radius R under the action of a central force. Potential due to the central force is given by V(r) = kr (k is a positive constant). Period of revolution of the body is proportional to-
R1/2
R−1/2
R3/2
R−5/2
The correct Answer is:A
Step by step video, text & image solution for A body moves in a circular orbit of radius R under the action of a central force. Potential due to the central force is given by V(r) = kr (k is a positive constant). Period of revolution of the body is proportional to- by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
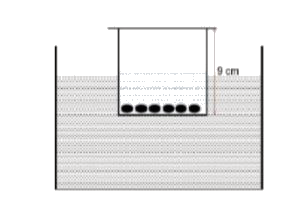
A wide bottom cylindrical massless plastic container of height 9 cm has 40 identical coins inside it and is floating on water with 3 cm inside the water. If we start putting more of such coins on its lid. It is observed that after N coins are put, its equilibrium changes from stable to unstable. Equilibrium in floating is stable if the geometric center of the submerged portion is above the center of mass of the object) The value of N is closed to
View SolutionA body of mass 2kg is moving under the influence of a central force whose potential energy is given by U=2r3J. If the body is moving in a circular orbit of 5m, its energy will be
View SolutionA particle moves in a circular orbit under the action of a central attractive force inversely proportional to the distance r. The speed of the particle is
View SolutionA particle of mass 9 kg is moving under the action of a central force whose potential energy is given by U=10/r For what energy it will orbit a circle of radius 10 m ? Calculate the time period of this motion
View SolutionA particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the nth power of R. If the period of rotation of the particle is T, then :
View Solutionएक कण R त्रिज्या के एक वृताकार पथ पर किसी एक केंद्रीय बल जो की R की n वि घाट के व्योककृमानुपाती है, के अंतर्गत घूमता है । यदि कण का आवर्तकाल t हो, तो :
View SolutionA particle moves in a circular orbit under the action of a central attractive force which is inversely proportional to the distance 'r' . The speed of the particle is
View SolutionA particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the n th power of R. If the period of rotation of the particle is T, then
View Solutionएक वस्तु r त्रिज्या की वृत्तीय कक्षा में केन्द्रीय आकर्षण बल क F=−kr,(kस्थिरांक है)। से गतिज है। वस्तु की गति का आवर्तकाल समानुपाती होगा|
View SolutionA particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the n^(th) power of R. If the period of rotation of the particle is T, then :
View SolutionIf the force acting on the body moving in uniform circular motion is inversely proportional to r3, then the time period of its revolution is proportional to ?
View SolutionA particle is moving with uniform speed along the circumference of a circle of radius R under the action of a central fictitious force F which is inversely proportional to R3. its time period of revolution will be given by :
View Solutionएक कृत्रिम उपग्रह, M द्रव्यमान और R त्रिज्या के ग्रह के चरों ओर r त्रिज्या की कक्षा में परिक्रमा कर रहा है। किसी केंद्रीय पिंड के चारोबन ओर परिक्रमा करते किसी उपग्रह के लिए, केप्लर के तृतीय नियमानुसार परिक्रमण काल T का वर्ग कक्षा की त्रिज्या r के घन के समानुपाती होता है। विमीय विश्लेषण विधि का उपयोग करके दर्शाइए,
T=kR√r3g, जहाँ k एक विमाविहीन नियतांक है और g केंद्रीय पिंड के गुरत्व के कारण त्वरण है।
View SolutionA particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the n^(th) power of R. If the period of rotation of the particle is T, then :
View SolutionA body moves in a circular orbit of radius R under the action of a central force. Potential due to the central force is given by V(r) = kr (k is a positive constant). Period of revolution of the body is proportional to-
View Solution
