An ideal gas has initial volume V and pressure p. In doubling its volume the minimum work done will be in the process (of the given processes)
(a) isobaric process
(b) isothermal process
(c) adiabatic process
(d) same in all given processes
The correct Answer is:C
To determine the process in which the minimum work is done when an ideal gas doubles its volume from an initial volume V and pressure P, we will analyze three different thermodynamic processes: isobaric, isothermal, and adiabatic.
1. Identify the Initial and Final States:
- Initial volume V1=V
- Final volume V2=2V
- Initial pressure P1=P
2. Understand the Types of Processes:
- Isobaric Process: The pressure remains constant. The work done W is given by:
W=PΔV=P(V2−V1)=P(2V−V)=PV
- Isothermal Process: The temperature remains constant. For an ideal gas, the work done is given by:
W=nRTln(V2V1)=nRTln(2)
- Adiabatic Process: No heat is exchanged with the surroundings. The work done can be derived from the first law of thermodynamics and is generally less than that of isothermal processes for the same change in volume.
3. Analyze the Work Done in Each Process:
- Isobaric Work: The work done is W=PV.
- Isothermal Work: The work done is W=nRTln(2). This is generally larger than the work done in an adiabatic process.
- Adiabatic Work: The work done is less than that of isothermal because the gas does not absorb heat. The exact expression for work done in an adiabatic process can be derived using the relation PVγ=constant, but it is known that it results in less work compared to isothermal and isobaric processes.
4. Conclusion:
- Among the three processes, the adiabatic process requires the least amount of work to double the volume of the gas. Therefore, the minimum work done occurs in the adiabatic process.
Final Answer:
The minimum work done will be in the adiabatic process.
- Initial volume V1=V
- Final volume V2=2V
- Initial pressure P1=P
- Isobaric Process: The pressure remains constant. The work done W is given by:
W=PΔV=P(V2−V1)=P(2V−V)=PV
- Isothermal Process: The temperature remains constant. For an ideal gas, the work done is given by:
W=nRTln(V2V1)=nRTln(2)
- Adiabatic Process: No heat is exchanged with the surroundings. The work done can be derived from the first law of thermodynamics and is generally less than that of isothermal processes for the same change in volume.
- Isobaric Work: The work done is W=PV.
- Isothermal Work: The work done is W=nRTln(2). This is generally larger than the work done in an adiabatic process.
- Adiabatic Work: The work done is less than that of isothermal because the gas does not absorb heat. The exact expression for work done in an adiabatic process can be derived using the relation PVγ=constant, but it is known that it results in less work compared to isothermal and isobaric processes.
- Among the three processes, the adiabatic process requires the least amount of work to double the volume of the gas. Therefore, the minimum work done occurs in the adiabatic process.
The minimum work done will be in the adiabatic process.
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 1 Objective Questions1videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 1 Subjective24videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEYCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 1 Assertion And Reason10videos
LAWS OF THERMODYNAMICS
- BOOK - DC PANDEYCHAPTER - LAWS OF MOTIONEXERCISE - Medical entrances gallery39videos
LAWS OF MOTION
- BOOK - DC PANDEYCHAPTER - MAGNETIC EFFECT OF CURRENT AND MAGNETISMEXERCISE - Integer type Questions10videos
MAGNETIC EFFECT OF CURRENT AND MAGNETISM
Similar Questions
Knowledge Check
- Question 1 - Select One
An ideal gas is initially at P1,V1 is expands to P2,V2 and then compressed adiabatically to the same volume V1 and pressure P3. If W is the net work done by the gas in complete process which of the following is true.
AW>0,P3>P1BW<0,P3>P1CW>0,P3<P1DW<0,P3<P1 - Question 2 - Select One
An ideal monatomic gas expands to twice its volume. If the process is isothermal, the magnitude of work done by the gas is W1. If the process is adiabatic, the magnitude of work done by the gas is Wa . Which of the following is true ?
AWi=Wa>0BWi>Wa=0CWi>Wa>0DWi>Wa>0 - Question 3 - Select One
16 g oxygen gas expands at STP to occupy double of its original volume. The magnitude of work done during the process is:
A260 calB180 calC130 calD271.6 cal
An ideal gas has initial pressure of 3 presssure units and an initial volume units the table gives the final pressure and volume of the gas ( in those same units ) in five processes which processes start and end on the same isotherm ?
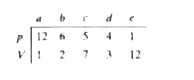 View Solution
View SolutionOne mole of an ideal gas at initial temperature T, undergoes a quasi-static process during which the volume V is doubled. During the process the internal energy U obeys the equation U=aV(3) where a is a constant. The work done during this process is-
View Solution1 liter of an ideal gas (γ=1.5) at 300k is suddenly compressed to half its original volume. (a) Find the ratio of the final pressure to the initial pressure. (b) If the original pressure is 100kpa, find the work done by the gas in the process. (c) What is the change in internal energy? (d) What is the final temperature? (e) the gas is now colled to 300k keeping its pressure constant. Calculate the work done during the process . (f) The gas is now expanded iasothermally to achive its original volume of 1 liters. Calculate the work done by the gas .(g) Calculate the total work done in the cycle.
View SolutionAn ideal diatomic gas is expanded so that the amount of heat transferred to the gas is equal to the decrease in its internal energy.
If in the above process, the initial temperature of the gas be T0 and the final volume by 32 times the initial volume, the work done ( in joules ) by the gas during the process will beView SolutionThe pressure of an ideal gas varies with volume as P= aV, where a is a constant. One mole of the gas is allowed to undergo expansion such that its volume becomes ‘m’ times its initial volume. The work done by the gas in the process is
View Solution