An ideal gas has initial volume V and pressure P . To triple it a volume the minimum work done will be in
Isothermal process
Adiabatic process
Isobaric process
Equal in all process
To solve the problem of finding the minimum work done to triple the volume of an ideal gas, we will analyze the work done during different thermodynamic processes: isobaric, isothermal, and adiabatic.
1. Understanding the Initial Conditions:
We have an ideal gas with an initial volume V and pressure P. We want to triple the volume, which means the final volume will be 3V.
2. Work Done in Thermodynamic Processes:
The work done W in a thermodynamic process can be calculated using the formula:
W=∫PdV
This means that the work done is equal to the area under the P vs. V curve for the process.
3. Analyzing Different Processes:
- Isobaric Process: In an isobaric process, the pressure remains constant. The work done can be calculated as:
Wisobaric=PΔV=P(3V−V)=2PV
- Isothermal Process: In an isothermal process, the temperature remains constant. The work done is given by:
Wisothermal=nRTln(VfVi)=nRTln(3)
(where n is the number of moles and R is the gas constant).
- Adiabatic Process: In an adiabatic process, no heat is exchanged with the surroundings. The work done can be derived from the first law of thermodynamics, but it is generally less than that of isothermal and isobaric processes for the same change in volume.
4. Comparing Work Done:
To find the minimum work done, we need to compare the work done in each process. The work done in the adiabatic process is less than that in the isothermal and isobaric processes for the same change in volume.
5. Conclusion:
The minimum work done to triple the volume of the gas will occur during the adiabatic process. Therefore, the answer is that the minimum work done will be in the adiabatic process.
Final Answer:
The minimum work done to triple the volume of the ideal gas will be in the adiabatic process.
---
We have an ideal gas with an initial volume V and pressure P. We want to triple the volume, which means the final volume will be 3V.
The work done W in a thermodynamic process can be calculated using the formula:
W=∫PdV
This means that the work done is equal to the area under the P vs. V curve for the process.
- Isobaric Process: In an isobaric process, the pressure remains constant. The work done can be calculated as:
Wisobaric=PΔV=P(3V−V)=2PV
- Isothermal Process: In an isothermal process, the temperature remains constant. The work done is given by:
Wisothermal=nRTln(VfVi)=nRTln(3)
(where n is the number of moles and R is the gas constant).
- Adiabatic Process: In an adiabatic process, no heat is exchanged with the surroundings. The work done can be derived from the first law of thermodynamics, but it is generally less than that of isothermal and isobaric processes for the same change in volume.
To find the minimum work done, we need to compare the work done in each process. The work done in the adiabatic process is less than that in the isothermal and isobaric processes for the same change in volume.
The minimum work done to triple the volume of the gas will occur during the adiabatic process. Therefore, the answer is that the minimum work done will be in the adiabatic process.
The minimum work done to triple the volume of the ideal gas will be in the adiabatic process.
Topper's Solved these Questions
Similar Questions
An ideal gas has initial pressure of 3 presssure units and an initial volume units the table gives the final pressure and volume of the gas ( in those same units ) in five processes which processes start and end on the same isotherm ?
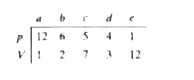
View SolutionAn ideal gas has pressure P, volume V and temperature T. Select the correct option.
View Solution
Knowledge Check
An ideal gas has initial volume V and pressure p. In doubling its volume the minimum work done will be in the process (of the given processes)
A(a) isobaric processB(b) isothermal processC(c) adiabatic processD(d) same in all given processesAn ideal gas of volume V and pressure P expands isothermally to volume 16 V and then compressed adiabatically to volume V . The final pressure of gas is [γ=1.5]
APB3PC4PD6P5 mole of an ideal gas of volume is expanded against vaccum to make its volume 2 times, then work done by the gas is:
A−RT(V2−V1)B−RTln(V2V1)C0DCv(T2−T1)
An ideal gas having initial pressure P, volume V and temperature T is allowed to expands adiabatically until its volume becomes 5.66V while its temperature falls to T/2.
(i) How many degrees of freedom do the gas molecules have?
Obtain the work done by the gas during the expansion as a function of the initial pressure P and volume V.
View SolutionAn ideal gas having initial pressure p, volume V and temperature T is allowed to expand adiabatically until its volume becomes 5.66V, while its temperature falls to T/2.
(a) How many degrees of freedom do the gas molecules have?
(b) Obtain the work done by the gas during the expansion as a function of the initial pressure p and volume V.
Given that (5.66)0.4=2
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermically to a volume 2V and a final pressure Pi, If the same gas is expanded adiabatically to a volume 2V, the final pressure Pa. The ratio of the specific heats of the gas is 1.67. The ratio PaP1 is .......
View SolutionAn ideal gas is initially at P1,V1 is expands to P2,V2 and then compressed adiabatically to the same volume V1 and pressure P3. If W is the net work done by the gas in complete process which of the following is true.
View SolutionAn ideal gas with pressure P, volume V and temperature T is expanded isothermally to a volume 2V and final pressure PI. The same gas is expanded adiabatically to a volume 2V and final pressure in this case is PA. In terms of the ratio of the two specific heats for the gas γ, the ratio PI/PA is
View Solution
