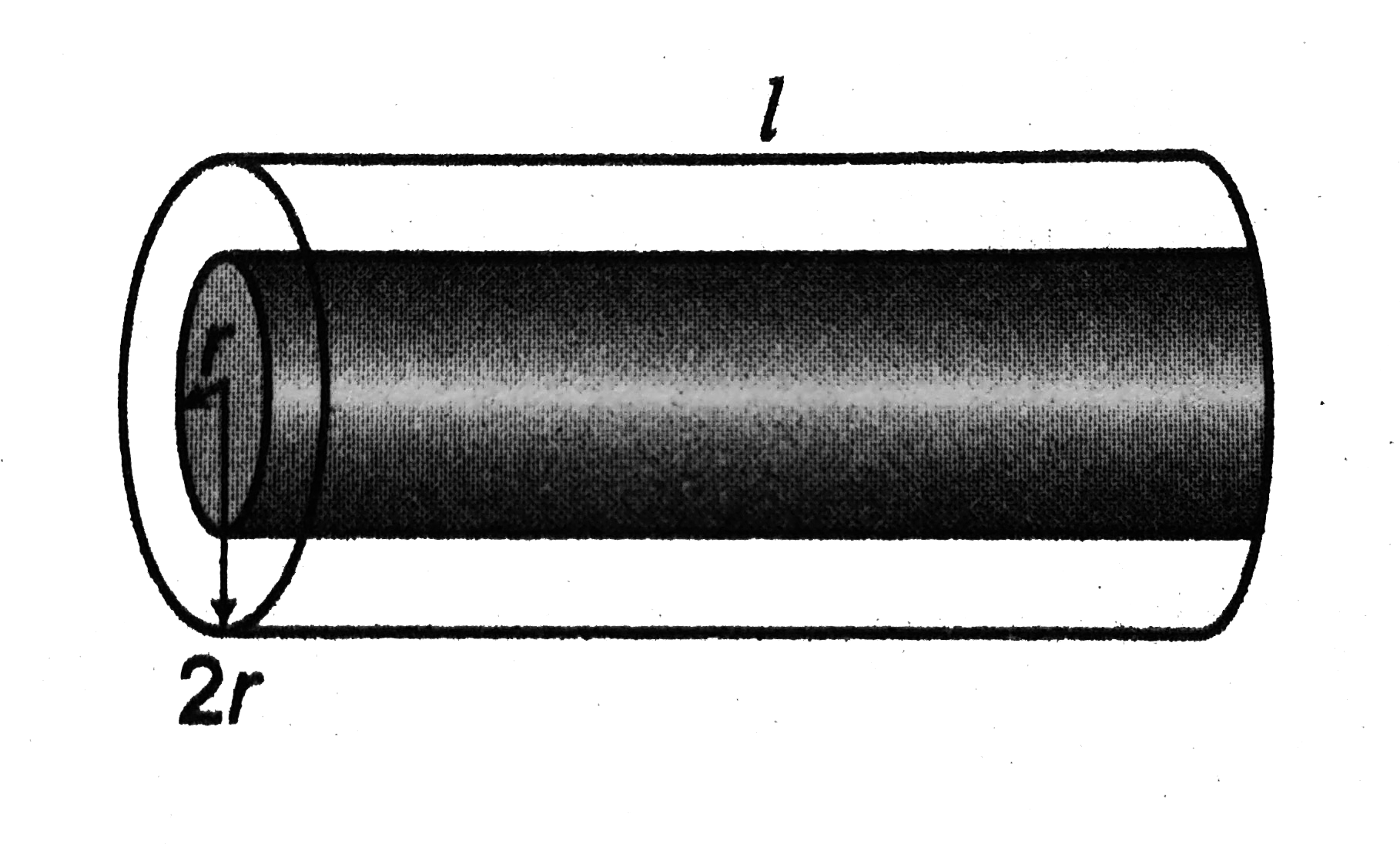
A cylinder of radius R made of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 2R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. The effective thermal conductivity of the system is
K1+K2
K1K2K1+K2
K1+3K24
3K1+K24
The correct Answer is:C
To find the effective thermal conductivity of the given system, we will analyze the problem step by step.
Step 1: Understand the Configuration
We have two cylindrical components:
1. A central cylinder with radius R and thermal conductivity K1.
2. A cylindrical shell surrounding the central cylinder with inner radius R and outer radius 2R and thermal conductivity K2.
Step 2: Identify the Heat Transfer Mechanism
Since the system is in a steady state and there is no heat loss across the cylindrical surfaces, we can treat the heat transfer through the two cylindrical components as being in parallel.
Step 3: Calculate the Resistance of Each Component
The thermal resistance R for a cylindrical object can be calculated using the formula:
R=LK⋅A
Where:
- L is the length of the cylinder,
- K is the thermal conductivity,
- A is the cross-sectional area.
For the inner cylinder (radius R):
- The cross-sectional area A1=πR2.
- Therefore, the thermal resistance R1 is given by:
R1=LK1⋅πR2
For the outer cylindrical shell (inner radius R and outer radius 2R):
- The cross-sectional area A2 is the difference between the outer and inner areas:
A2=π(2R)2−πR2=π(4R2−R2)=3πR2
- Therefore, the thermal resistance R2 is given by:
R2=LK2⋅3πR2
Step 4: Calculate the Total Resistance in Parallel
Since the resistances are in parallel, the total thermal resistance Rtotal can be calculated using:
1Rtotal=1R1+1R2
Substituting the values of R1 and R2:
1Rtotal=K1⋅πR2L+K2⋅3πR2L
Factoring out common terms:
1Rtotal=πR2L(K1+3K2)
Step 5: Find the Effective Thermal Conductivity
The effective thermal conductivity Keff can be related to the total resistance:
Rtotal=LKeff⋅Atotal
Where Atotal=π(2R)2=4πR2.
Thus:
1Rtotal=Keff⋅4πR2L
Equating the two expressions for 1Rtotal:
πR2L(K1+3K2)=Keff⋅4πR2L
Cancelling πR2L from both sides:
K1+3K2=4Keff
Step 6: Solve for Keff
Rearranging gives:
Keff=K1+3K24
Final Answer
The effective thermal conductivity of the system is:
Keff=K1+3K24
---
We have two cylindrical components:
1. A central cylinder with radius R and thermal conductivity K1.
2. A cylindrical shell surrounding the central cylinder with inner radius R and outer radius 2R and thermal conductivity K2.
Since the system is in a steady state and there is no heat loss across the cylindrical surfaces, we can treat the heat transfer through the two cylindrical components as being in parallel.
The thermal resistance R for a cylindrical object can be calculated using the formula:
R=LK⋅A
Where:
- L is the length of the cylinder,
- K is the thermal conductivity,
- A is the cross-sectional area.
- The cross-sectional area A1=πR2.
- Therefore, the thermal resistance R1 is given by:
R1=LK1⋅πR2
- The cross-sectional area A2 is the difference between the outer and inner areas:
A2=π(2R)2−πR2=π(4R2−R2)=3πR2
- Therefore, the thermal resistance R2 is given by:
R2=LK2⋅3πR2
Since the resistances are in parallel, the total thermal resistance Rtotal can be calculated using:
1Rtotal=1R1+1R2
Substituting the values of R1 and R2:
1Rtotal=K1⋅πR2L+K2⋅3πR2L
Factoring out common terms:
1Rtotal=πR2L(K1+3K2)
The effective thermal conductivity Keff can be related to the total resistance:
Rtotal=LKeff⋅Atotal
Where Atotal=π(2R)2=4πR2.
1Rtotal=Keff⋅4πR2L
πR2L(K1+3K2)=Keff⋅4πR2L
K1+3K2=4Keff
Rearranging gives:
Keff=K1+3K24
The effective thermal conductivity of the system is:
Keff=K1+3K24
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Example Type 14videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Example Type 22videos
CALORIMETRY & HEAT TRANSFER
- BOOK - DC PANDEYCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise13videos
BASIC MATHEMATICS
- BOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery38videos
CALORIMETRY AND HEAT TRANSFER
Similar Questions
A cylinder of radius R made of a material of thermal conductivity K1 is surrounded by cylindrical shell of inner radius R and outer radius 2R made of a material of thermal con-ductivity K2 The two ends of the combined system are maintained at two differnet tem-peratures There is no loss of heat across the cylindrical surface and system is in steady state What is the effective thermal conductivity of the system
 .View Solution
.View SolutionA cylinder of radius R, made up of a material (thermal conductivity k1) is surrounded by a cylindrical sheet of inner radius R and outer radius 2R (thermal conductivity k2). The two ends of the combined system are maintained at two different temperatures. There is no loss of heat across the cylindrical surface and the system is in steady state. Calculate the effective thermal conductivity of the system.
View Solution
Knowledge Check
- Question 1 - Select One
A cylinder of radius R made of material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius R and outer radius 3R made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperatures. What is the effective thermal conductivity of the system ?
AK1+K2BK1+8K29CK1K2K1+K2D8K1+K29 - Question 2 - Select One
A cylinder A of a material of thermal conductivity K1 is surrounded by a cylindrical shell of inner radius equal to the cylinder. The shell is made of a material of thermal conductivity K2. The two ends of the combined system are maintained at two different temperature. if the effective thermal conductivity of the system is 4K1+5K29, find the rate of outer radius of the shell to the radius of the cylinder.
 A2.0B5/2C5/3D3/2
A2.0B5/2C5/3D3/2 - Question 3 - Select One
The ends of a rod of uniform thermal conductivity are maintained at different (constant) temperatures. Afer the steady state is achieved:
Aheat flows in the rod from high temperature to low temperature even if the rod has nonuniform cross sectional area.Btemperature gradient along length is same even if the rod has non uniform cross sectional area.Cheat current is same even if the rod has nono-uniform cross sectional areaDif the rod has uniform cross sectional area the temperature is same at all points of the rod.
A cylinder of radius R is surrounded by a cylindrical shell of inner radius R and oputer radius 2R. The thermal conductivity of the material of the inner cylinder si k1 and that of the outer cylinder is K2 ,Assumming no loss of heat , the effective thermal conductivity of the system for heat flowing along the length of the cylionder is :
View SolutionThermal conductivity of inner core of radius r is K and of the outer one of radius 2r is 2K. Find equivalent value of thermal conductivity between its two ends.
 View Solution
View SolutionCalculated thermal conductance for radial flow of a spherical sheel of inner and outer radius r1and r2. Assume that thermal conductivity of the material is K
View SolutionA metallic cylindrical shell of length 50 cm has inner radius of 3 cm and outer radius of 6 cm. If the inner and outer surfaces of the cylinder are maintained at 0∘C and 80∘C , respectively, then find the rate of flow of heat from the outer surface to the inner surface. Take, thermal conductivity of metal =69.3Wm−1k−1
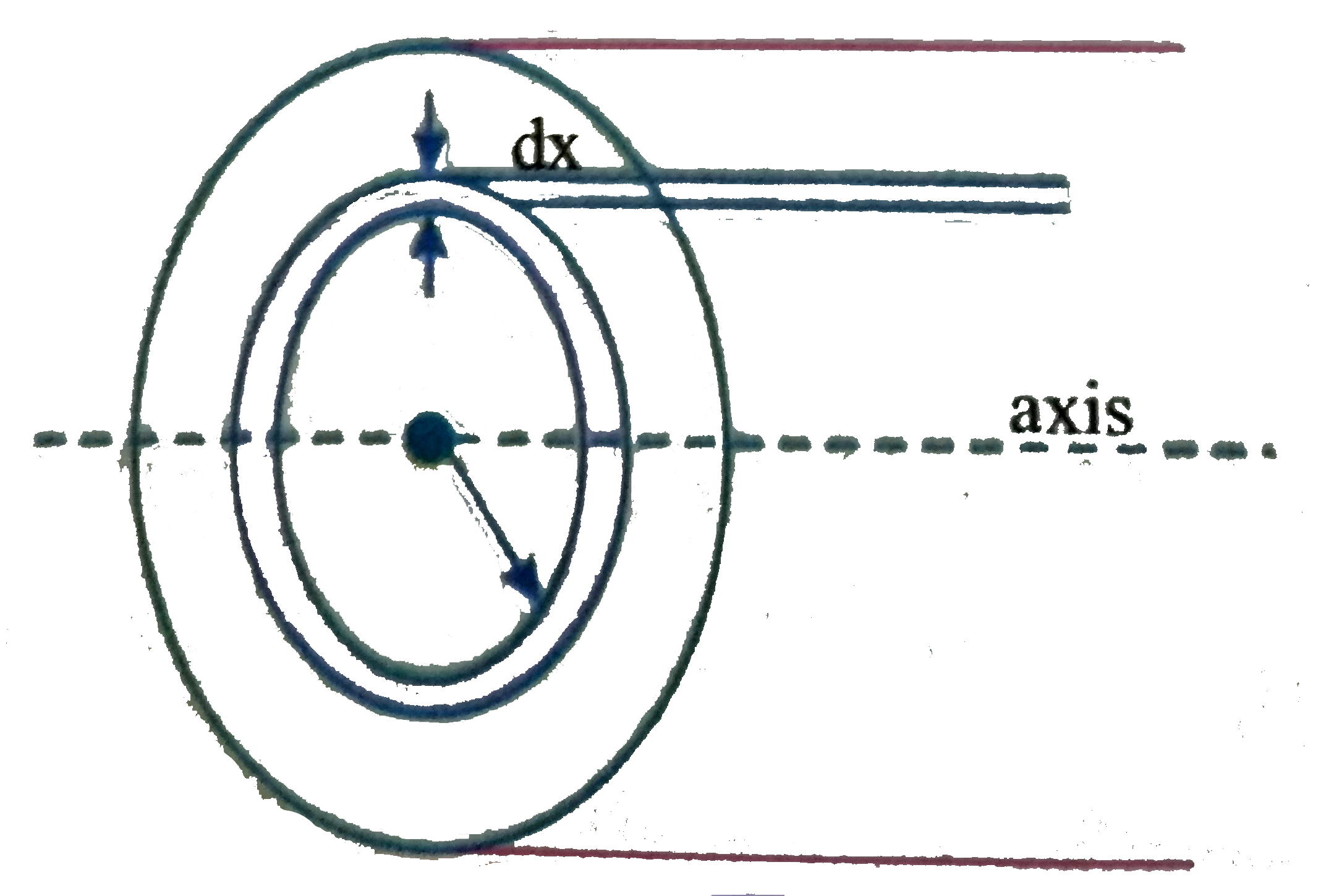
View SolutionA cylinder of radius R and length l is made uo of a substnace whose thermal conductivity K varies with the distance x from the axis as K=K1x+K2 Detemine the effective thermal conductivity between the flat faces of the cylinder
 .View Solution
.View Solution

