Assertion: Discharging graphs of two C.R. circuits having the same value of C is shown in figure. From the graph we can say that $τ_{C_{1}} > τ_{C_{2}}$

Reason: $R_{1} > R_{2}$

A

If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.

B

If both Assertion and Reason are true but Reason is not the correct explanation of Assertion.

C

If Assertion is true, but the Reason is false.

D

If Assertion is false but the Reason is true.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

In graph 1 , discharging is slow.
Hence $τ_{C_{1}} > τ_{C_{2}}$
Further,
$τ_{C} = C R$
$τ_{C} \propto R (a s C = c o n s tan t)$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One or More
In the L-C-R circuit as shown in figure,

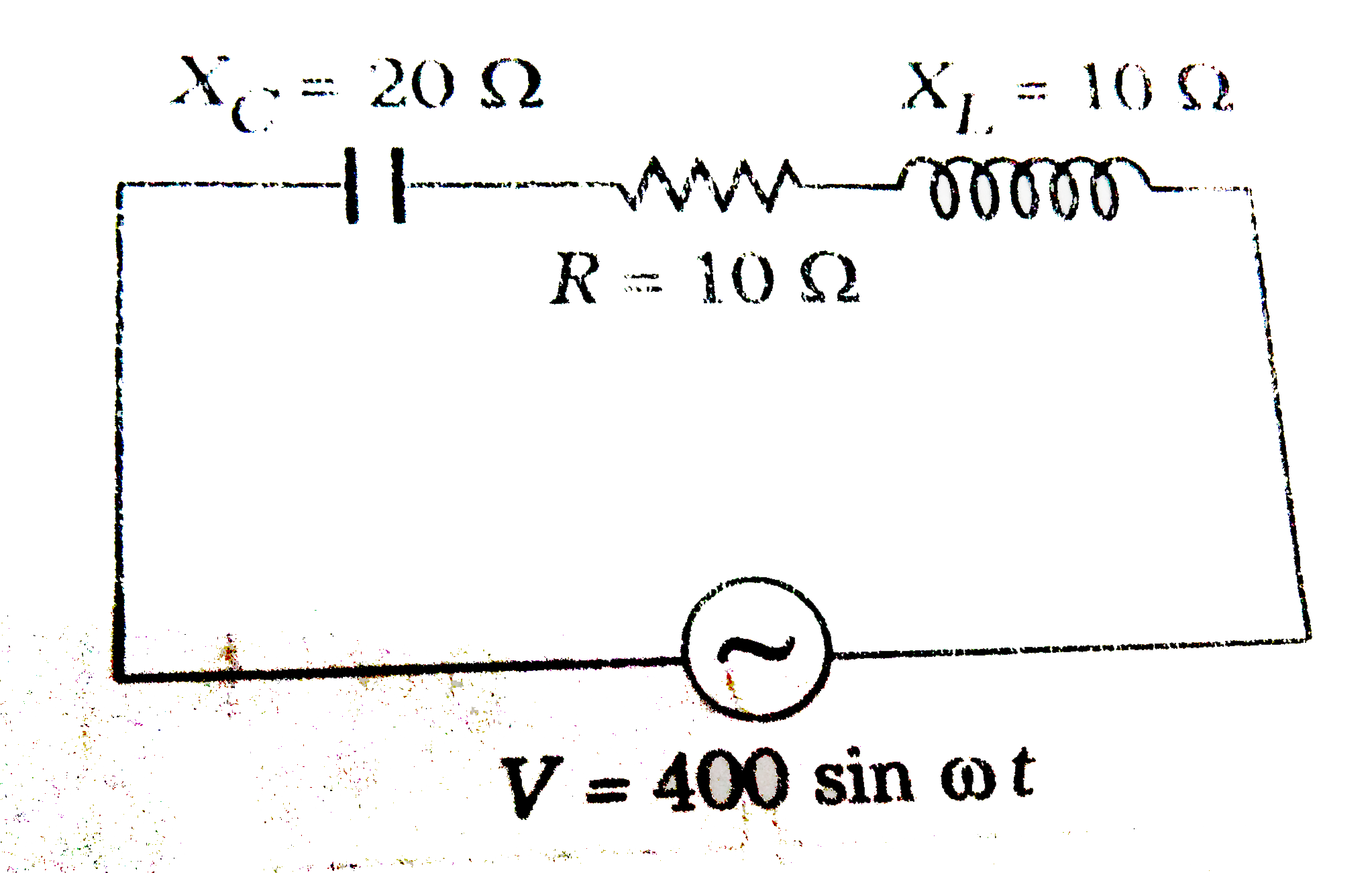ACurrent will lead the voltage
BRuns value of current is 20 A
CPower factor of the circuit is $\frac{1}{\sqrt{2}}$
DVoltage drop across resistance is 200 V
Question 2 - Select One
The charge across the capacitor in two different $R C$ circuit $1$ and $2$ are potted as shown in figure.

Identify the correct statement $(s)$ related to the $R_{1}, R_{2}, C_{1}$ and $C_{2}$ of the two $R C$ circuit-
A $R_{1} > R_{2}$ if $E_{1} = E_{2}$
B $C_{1} < C_{2}$ if $E_{1} = E_{2}$
C $R_{1} C_{1} > R_{2} C_{2}$
D $\frac{R_{1}}{R_{2}} < \frac{C_{2}}{C_{1}}$
Question 3 - Select One
In the circuit shown in the figure $X_{L} = \frac{X_{C}}{2}) = R$ the peck value current $i_{0}$ is
AAn inductor of 0.103H
BAn inductor of 0.25H
CA resistance of $6 . Ω$
DA resistance of $100 Ω$

DC PANDEY-CAPACITORS-Exercise

Home
Ask Doubt
Profile