A uniformly charged non conducting disc with surface charge density 10nC/m2 having radius R=3cm. Then find the value of electric field intensity at a point on the perpendicular bisector at a distance of r=2cm
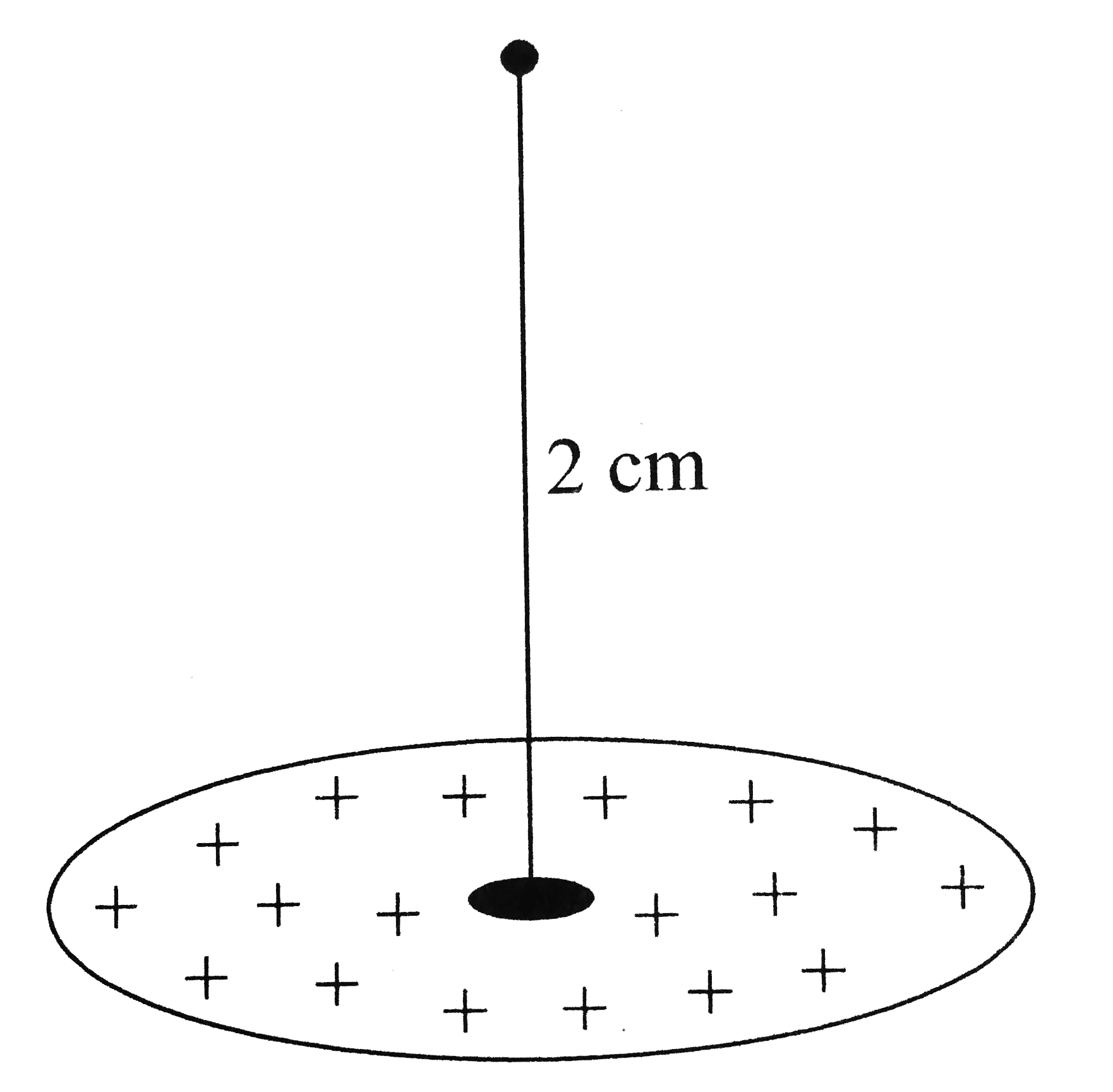
E=k6.2π[1−x√R2+x2]
E=9×109×10×10−9×6.28[1−x√4+9]
E=90×6.28[1−2√13]
E=251.2N/C
Topper's Solved these Questions
Similar Questions
" Electric field intensity due to a point charge " "q" ' at a distance 'r' from it is "
View SolutionA uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View Solution
Knowledge Check
- Question 1 - Select One
Two charges 10μCand−10μC are placed at points A.andB separated by a distance of 10 cm. Find the electric field at a point P on the perpendicular bisector of AB at. a distance of 12 cm from its middle point.
A4.1×106N/CB2.2×106N/CC4.1×105N/CD2.2×105N/C - Question 2 - Select One
For a uniformly charged non conducting sphere of radius R which of following shows a correct graph between the electric field intensity and the distance from the centre of sphere –
A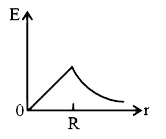 B
B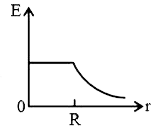 C
C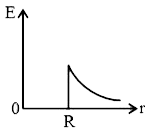 D
D
- Question 3 - Select One
Find the electric field intensity due to a positively charged conducting cylinder with radius 1 cm and surface charge density 10−9C/m2, at a point at a distance of 2 m from the axis of cylinder. The dielectric constant of the medium surrounding the cylinder is 2.
A0.28V/mB1.28V/mC2.28V/mD1.00V/m
Find : (i)Electric field intensity due to an infinitely long uniformly charged, straight conductor , at a perpendicular distance d from rod.
(ii)Electric field intensity at a point on perpendicular bisector of uniformly charged rod of length l and charge Q at a distance d from the centre of rod.View SolutionA uniformly charged conducting sphere is having radius 1 m and surface charge density 20 Cm−2. The total flux leaving the Gaussian surface enclosing the sphere is
View SolutionCalculate the magnitude of electric field intensity at a point 10 cm away from a line charge of linear charge density 5 μC/m.
View SolutionDerive an expression for the strength of electric field intensity at a point on the axis of a uniformly charged circular coil of radius R carrying charge Q.
View SolutionA Uniformly charged solid non-conducting sphere of uniform volume charge density ρ and radius R is having a concentric spherical cavity of radius r. Find out electric field intensity at following points, as shown in the figure :

(i) Point A (ii) Point B
(iii) Point C (iv) Centre of the sphereView Solution

