Assertion: →E=Exˆi+Eyˆj+Ezˆk,→V×→E=0
Resion Ex,Ey,Ez is independent.
If both assertion and reason are true and reason is the correct explanation of assertion.
If both assertion and reason are true but reason is not the correct explanation of assertion.
If assertion is true but reason is false.
If both assertion and reason are false.
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
An electron (mass m ) with initival velocity →v=v0ˆi+v0ˆj is the an electric field →E=−E0ˆk . It λ0 is initial de - Broglie wavelength of electron, its de-Broglie wave length at time t is given by :
View SolutionAn electron (mass m ) with initival velocity →v=v0ˆi+v0ˆj is the an electric field →E=−E0ˆk . It λ0 is initial de - Broglie wavelength of electron, its de-Broglie wave length at time t is given by :
View Solution
Knowledge Check
If unifrom electric filed →E=E0ˆi+2E0ˆj, where E0 is a constant, exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,0) will be.
AzeroB−E0x0C−2E0x0D−√5E0x0The displacement of a chrage Q in the electric field
E=e1ˆi+e2ˆj+e3ˆk is →r=aˆi+bˆj. The work done isAQ(ae1+be2)BQ√(ae21)+(be22)CQ(e1+e2)√a2+b2DQ(√e21+e22)(a+b)An electron is travelling with a constant velocity →v=v0ˆj in the presence of a uniform electric field →E=E0ˆk, where E0=mge (Here, m denotes the mass of the electron and e denotes its charge g denotes the acceleration due to gravity). Gravity acts in the -Z direction. At t=0, when the electron is at the origin, a uniform magnetic fiedl →B=Bxˆi+Byˆj is switched on. Here Bx and By are fixed positive constants and B0=√B2x+B2y. The coordinates of the point whre the electron intersects the first time after t=0 are given by:
A(2πmv0e(B2xB30),2πmv0e(BxByB30))B(2πmv0e(BxByB30),2πmv0e(BxByB30))C(2πmv0e(B2xB30),2πmv0e(B2yB30))D(2πmv0e(BxByB30),2πmv0e(B2yB30))
If unifrom electric filed →E=E0ˆi+2E0ˆj, where E0 is a constant, exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,0) will be.
View SolutionLet V0 be the potential at the origin in an electric field →E=Exˆi+Eyˆj. The potential at the point (x,y) is
View SolutionA particle of charge q, mass starts moving from origin under the action of an electric field →E=E0ˆi and magnetic field →B=B0ˆk . Its velocity at (x,0,0) is v0(6ˆi+8ˆj). The value of x is
View SolutionLet V0 be the potential at the origin in an electric field →E=Exˆi+Eyˆj. The potential at the point (x,y) is
View SolutionDue to a charge inside the cube, the electric field is: Ex = 600x, Ey = 0, Ez = 0. The charge inside the cube is nearly -
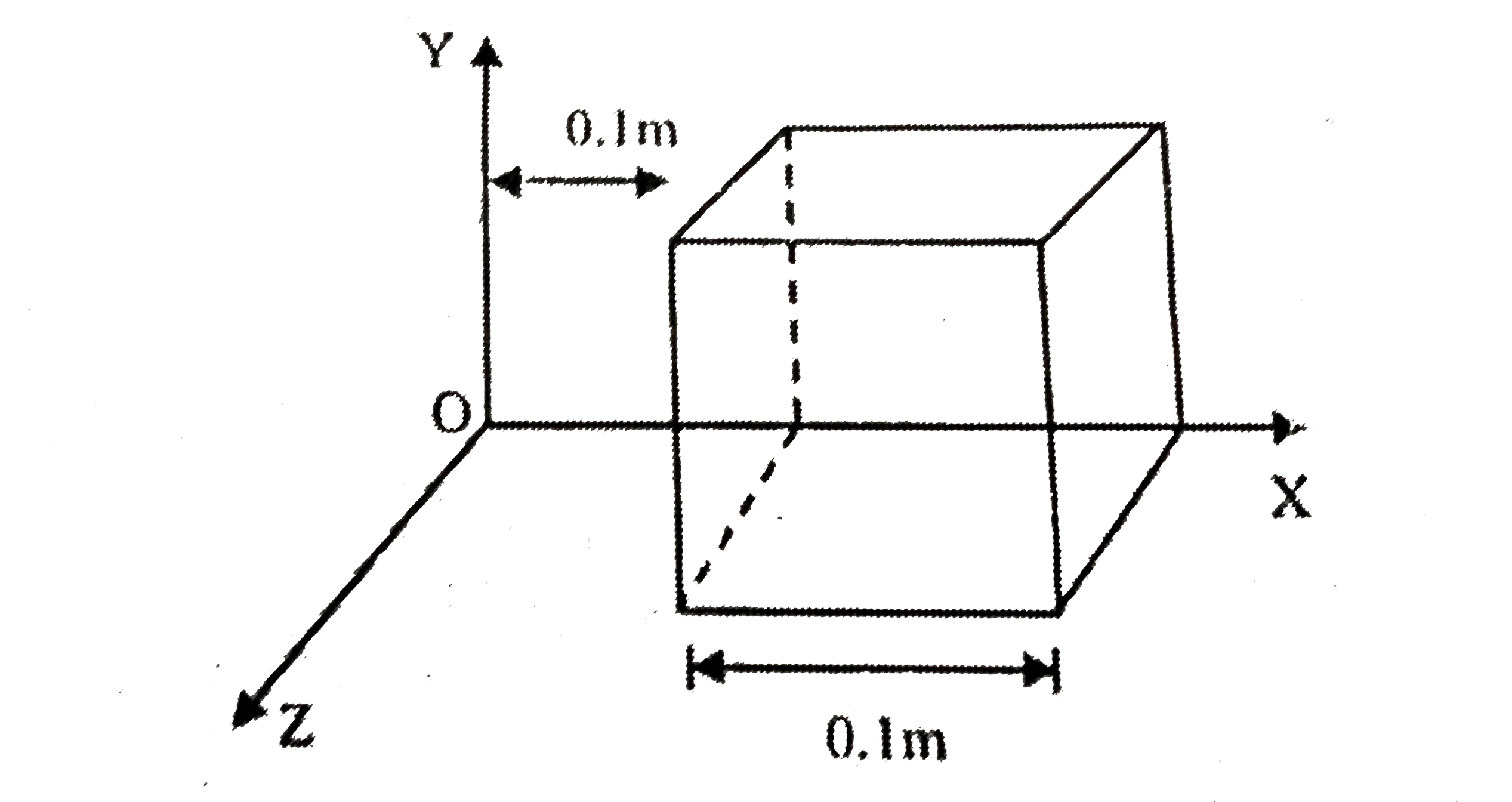
View Solution
