If unifrom electric filed →E=E0ˆi+2E0ˆj, where E0 is a constant, exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,0) will be.
Zero
−E0x0
−2E0x0
−√5E0x0
The correct Answer is:B
To solve the problem, we need to find the electric potential at the point (x0,0) given that the electric potential at the origin (0,0) is zero and the uniform electric field is →E=E0^i+2E0^j.
1. Understand the Electric Field:
The electric field is given as →E=E0^i+2E0^j. This means:
- The electric field in the x-direction, Ex=E0.
- The electric field in the y-direction, Ey=2E0.
2. Use the Relation Between Electric Field and Potential:
The relationship between electric field and electric potential is given by:
Ex=−dVdx
This implies:
Exdx=−dV
3. Calculate the Change in Potential:
We want to find the potential at the point (x0,0). Since the potential at the origin (0,0) is V(0,0)=0, we can express the change in potential as:
dV=−Exdx
Here, dx is the change in the x-coordinate from 0 to x0, so dx=x0−0=x0.
4. Substitute the Values:
Substitute Ex=E0 into the equation:
dV=−E0dx
Therefore, we have:
dV=−E0x0
5. Find the Potential at (x0,0):
The potential at point (x0,0) can be expressed as:
V(x0,0)=V(0,0)+dV
Since V(0,0)=0, we get:
V(x0,0)=0−E0x0=−E0x0
Final Answer:
The potential at the point (x0,0) is:
V(x0,0)=−E0x0
The electric field is given as →E=E0^i+2E0^j. This means:
- The electric field in the x-direction, Ex=E0.
- The electric field in the y-direction, Ey=2E0.
The relationship between electric field and electric potential is given by:
Ex=−dVdx
This implies:
Exdx=−dV
We want to find the potential at the point (x0,0). Since the potential at the origin (0,0) is V(0,0)=0, we can express the change in potential as:
dV=−Exdx
Here, dx is the change in the x-coordinate from 0 to x0, so dx=x0−0=x0.
Substitute Ex=E0 into the equation:
dV=−E0dx
Therefore, we have:
dV=−E0x0
The potential at point (x0,0) can be expressed as:
V(x0,0)=V(0,0)+dV
Since V(0,0)=0, we get:
V(x0,0)=0−E0x0=−E0x0
The potential at the point (x0,0) is:
V(x0,0)=−E0x0
Topper's Solved these Questions
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.3
20 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.4
15 Videos
- ELECTRIC POTENTIALBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC POTENTIALEXERCISE - DPP 3.1
14 Videos
- ELECTRIC FLUX AND GAUSS LAWBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s
38 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
Similar Questions
If uniform electric field →E=E0ˆi+2E0ˆj, where E0 is a constant exists in a region of space and at (0,0) the electric potential V is zero, then the potential at (x0,2x0) will be -
View SolutionConisder an electric field →E=E0ˆx where E0 is a constant .
The flux through the shaded area (as shown in the figure) due to this field is
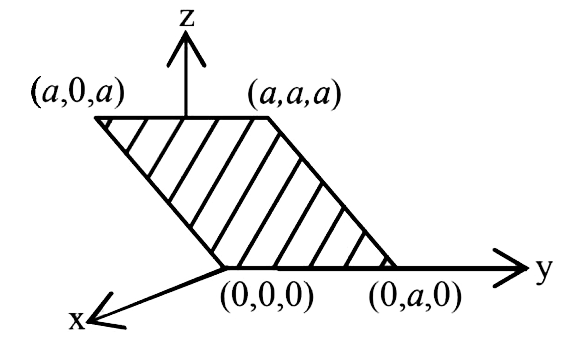
View SolutionA cube of side a is placed in a uniform electric field E=E0ˆi+E0ˆj+E0k. Total electric flux passing through the cube would be
View SolutionAn electric field E=(20ˆi+30ˆj) N/C exists in the space. If the potential at the origin is taken be zero, find the potential at (2m,2m).
View SolutionA particle of charge q and mass m is subjected to an electric field E=E0(1−ax2) in the x - direction, where a and E0 are constants. Initially the particle was at rest at x = 0. Other than the initial position the kinetic energy of the particle becomes zero when the distance of the particle from the origin is :
View SolutionAssume that an electric field →E=30x2ˆi exists in space. Then the potential differences VA−V0 where V0 is the potential at the origin and VA, the potential at x=2m is
View SolutionA uniform electric field E0 exists in a region at angle 45∘ with the x - axis. There are two point A(a,0)andB(0,b) having potential VAandVB, respectively, then
 .
.
View SolutionA unifrom electric field having a magnitude E0 and direction along the positive X-axis exists. If the protential V is zero at x=0, then its value at X=+x will be
View SolutionIn a certain region of space the electric potential V is known to be constant. Is the electric field in this region (a) positive (b) zero ,or (c ) negative ?
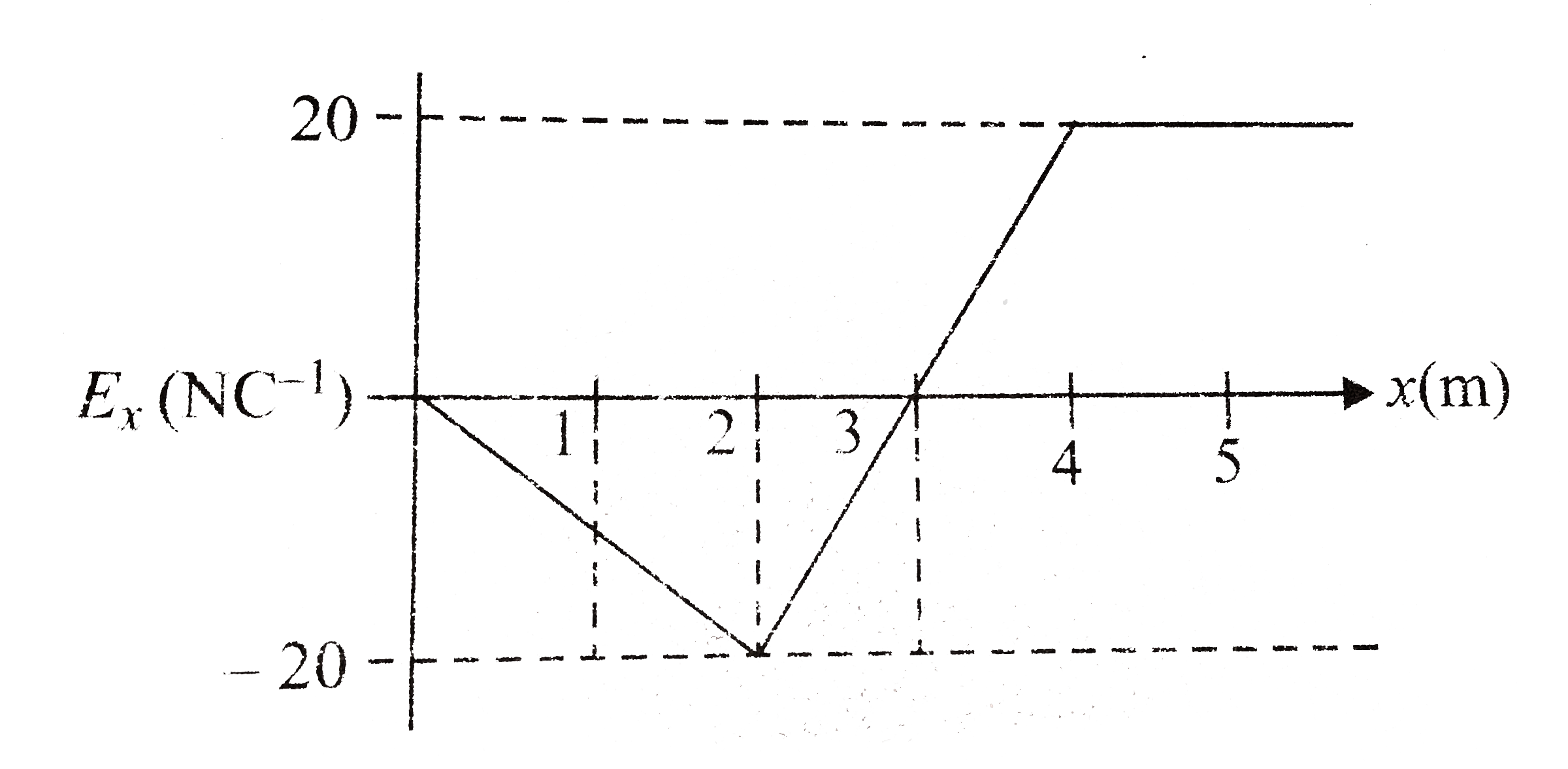
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
View Solution
