Initially spring is in natural length and both blocks are in rest condition. Then deter mine
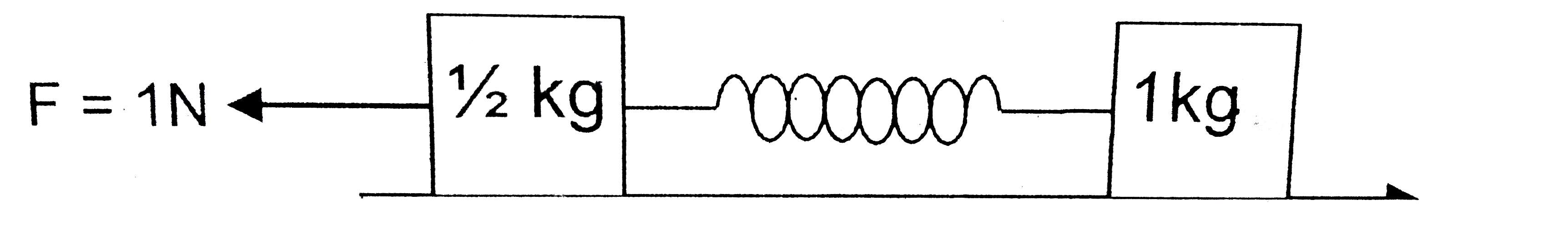
maximum extension in spring . K = 20 N/M
203cm
103cm
403cm
193cm
The correct Answer is:A
a=Fm1+m2
By work - energy theorem
(F−m1a)x1+(m2a)x2−12k(x1+x2)2=0
m2×Fm1+m2(x1+x2)=K2(x1+x2)2
(x1+x2)=m2×Fm1+m2×2k
=1×11.5×220=115m=10015cm=203cm
Topper's Solved these Questions
Similar Questions
Two bolcks A & B are connected by a spring of stiffness 512N/m and placed on a smooth horizontal surface. Initially the spring has its equilibrium length. The indicated velocities are imparted to A & B. Find the maximum extension in the spring?
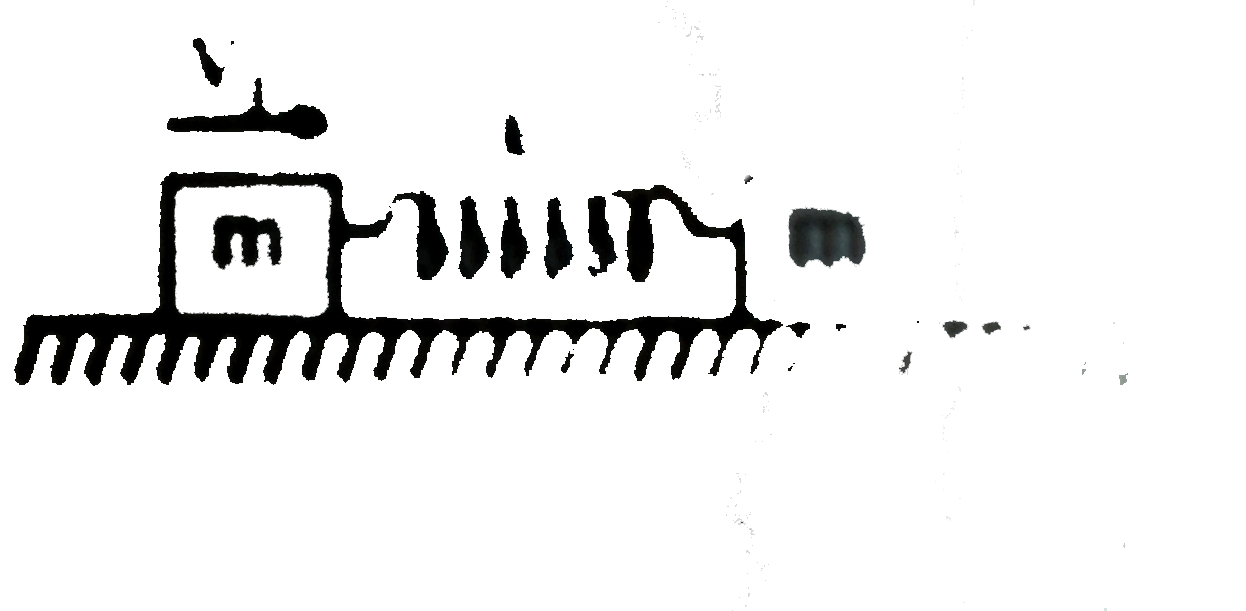
View SolutionTwo blocks A and B of masses m & 2m placed on smooth horizontal surface are connected with a light spring. The two blocks are given velocities as shown when spring is at natural length.
(i) Find velocity of centre of mass (b) maximum extension in the spring
View Solution
Knowledge Check
Initially spring is at it's natural length and collision is elastic. Then find maximum compression of spring during motion :
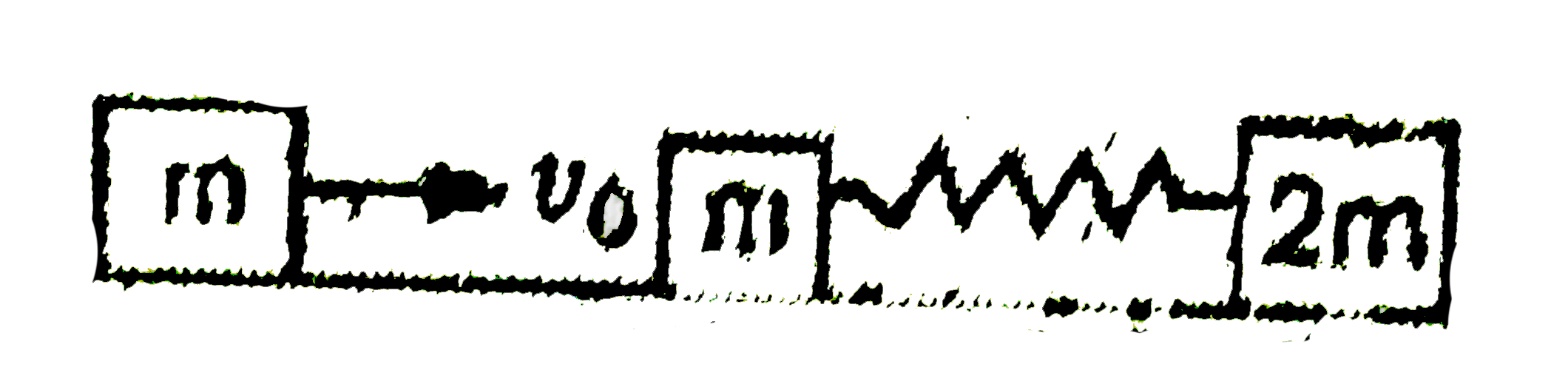A√2m3kυ0B√3m2kυ0C√m2kυ0D√mkυ0The system is released from rest with spring intially in its natural length. If mass of the block m = 10 kg. and spring constant k=100N/m, then maximum extension in spring is :
A1 mB12mC2 mD2.5 mBlock A of mass m is placed on a plank B. A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initially spring is in its natural length. If the plank B is given an acceleration a, then maximum compression in the spring is xmak. Find the value of x (All the surface are smooth)
A12B2C1D4
A system consists of block A and B each of mass m connected by a light spring as shown in the figure with block B in contact with a wall. The block A compresses the spring by 3mg/k from natural length of spring and then released from rest. Neglect friction anywhere.
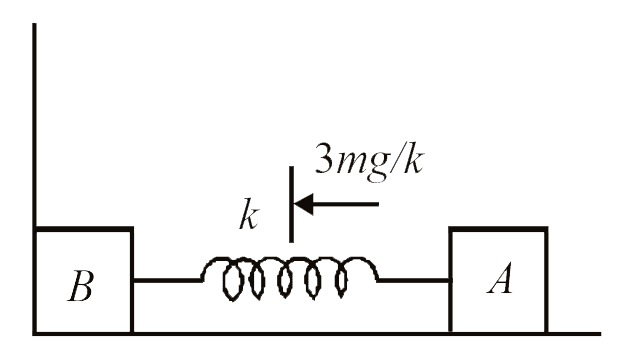
Maximum extension in the spring after system loses contact with wall
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
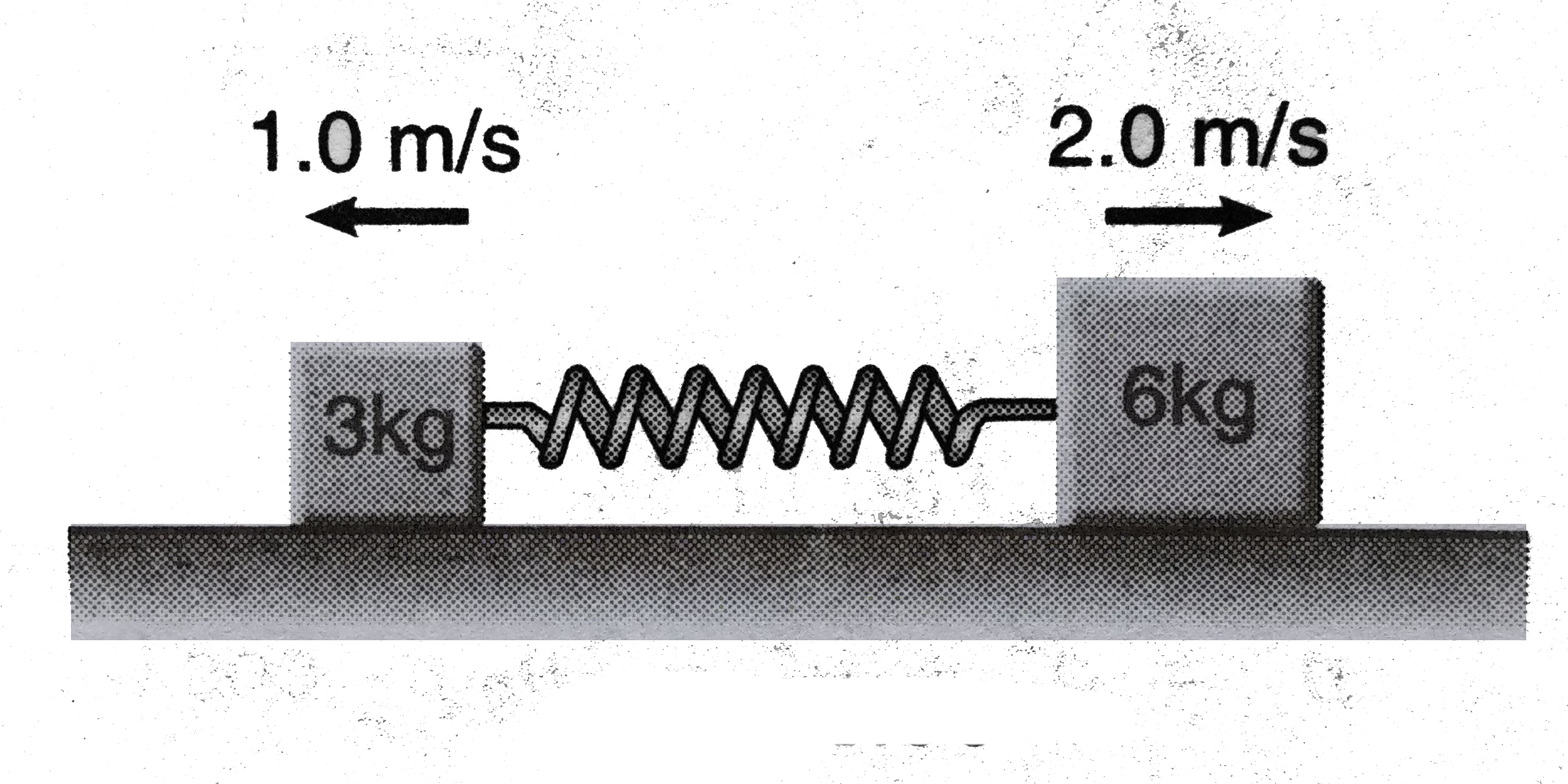
View SolutionA block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
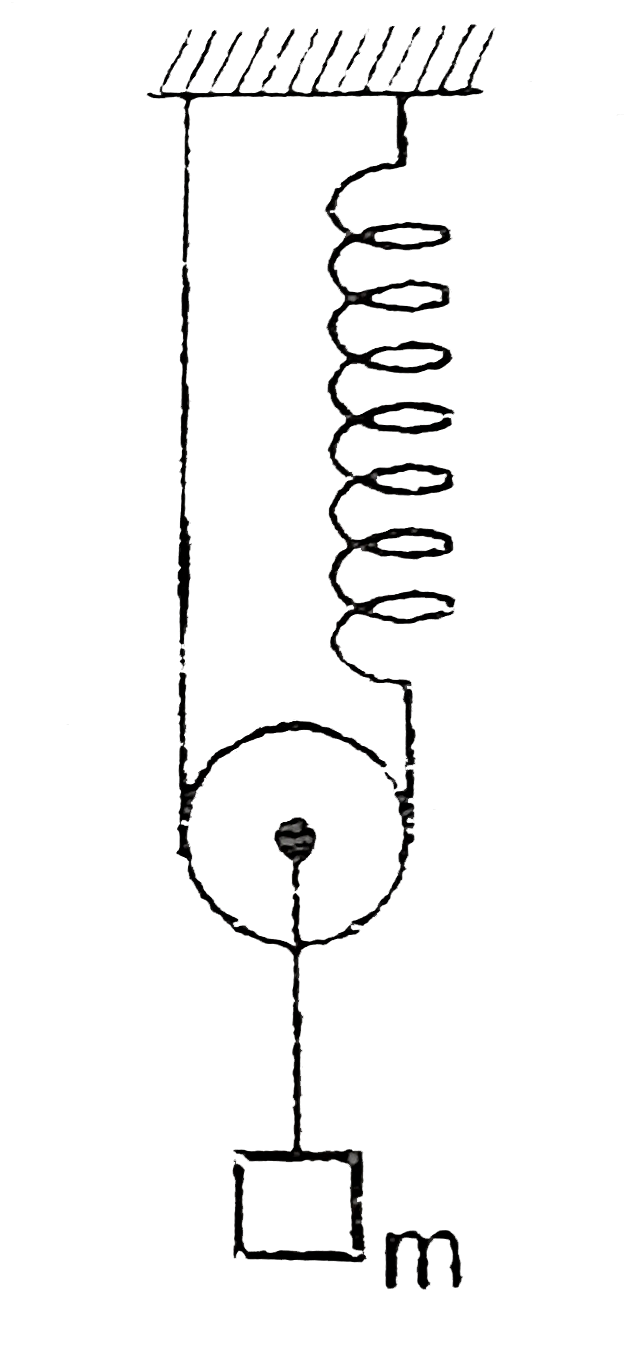
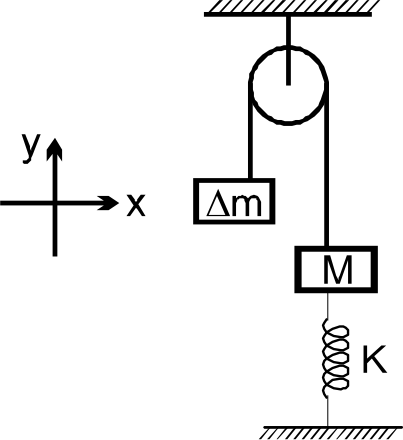
View SolutionConsider the system shown in figure. Pulley, string and spring are ideal and Δm<<M. Initially spring is in it’s natural length and both the blocks are at rest. (Assume that initially Δm was situated at origin). Maximum y coordinate of Δm in subsequent motion is xmg/k then value of x is .
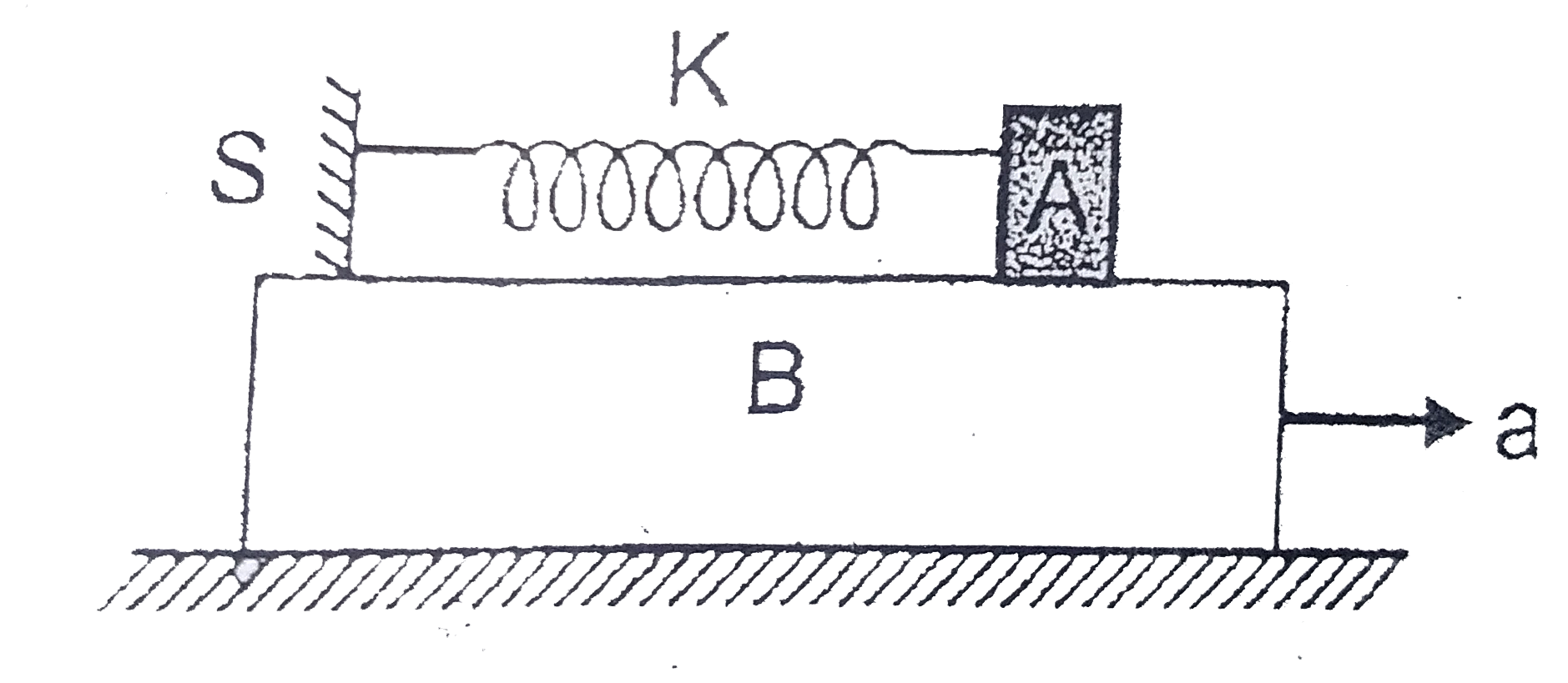
View SolutionBlock A of mass m is placed on a plank B . A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initialy spring is in the natural length, and the system is at rest. Find the maximum compression in the spring, if the plank B is moved with a constant acceleration 'a' . (All the surface are smooth) :
View Solution