Two bolcks A & B are connected by a spring of stiffness 512N/m and placed on a smooth horizontal surface. Initially the spring has its equilibrium length. The indicated velocities are imparted to A & B. Find the maximum extension in the spring?
The correct Answer is:25m
Using centre of mass frome of refrence, we can say that
12μv2rel=12kx2 [Here μ=m1m2m1+m2 (Reduced mass)]
⇒(3×63+6)(1.8+2.2)2=512x2
⇒(2)(4)2=512x2
⇒x=14m=25m
Topper's Solved these Questions
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-A) (JEE-ADVANCED Previous Year Questions)
11 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-4 (SECTION-A) (Comprehension)
3 Videos
- CENTRE OF MASS & MOMENTUM CONSERVATIONBOOK - BANSALCHAPTER - CENTRE OF MASS & MOMENTUM CONSERVATIONEXERCISE - EXERCISE-2[MATRIX TYPE]
2 Videos
- GRAVITATIONBOOK - BANSALCHAPTER - GRAVITATIONEXERCISE - EXERCISE -4 Section - B
6 Videos
Similar Questions
Two blocks A(3kg) and B(6kg) are connected by a spring of stiffness 512 N/m and placed on a smooth horizontal surface. Initially the spring has its equilibrium length. Velocities 1.8m/s and 2.2 m/s are imparted to A and B in opposite direction. The maximum extension in the spring will be –
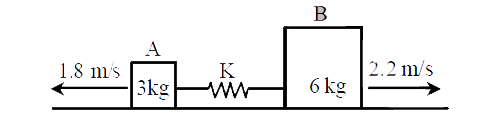
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
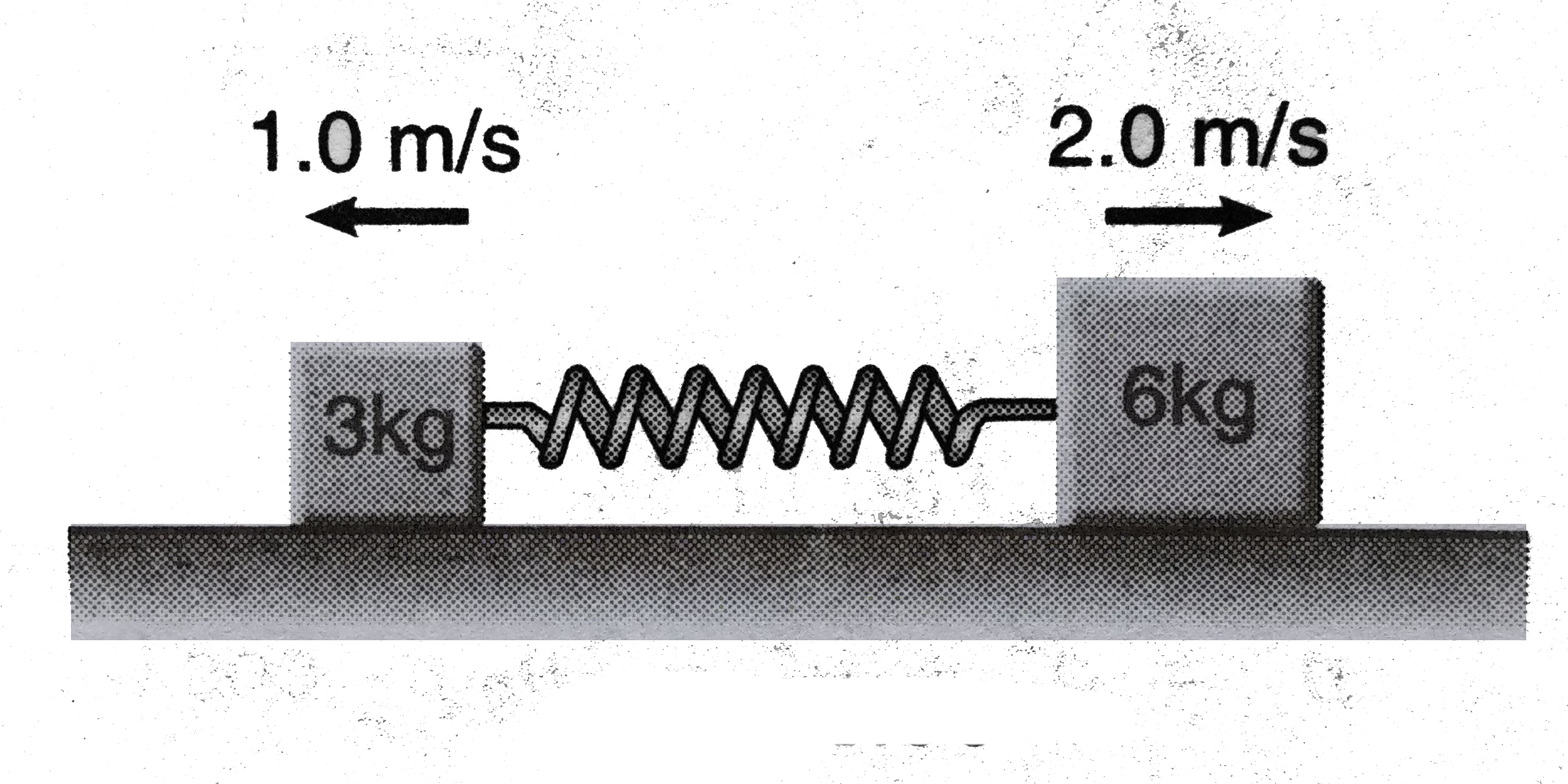
View Solution
Knowledge Check
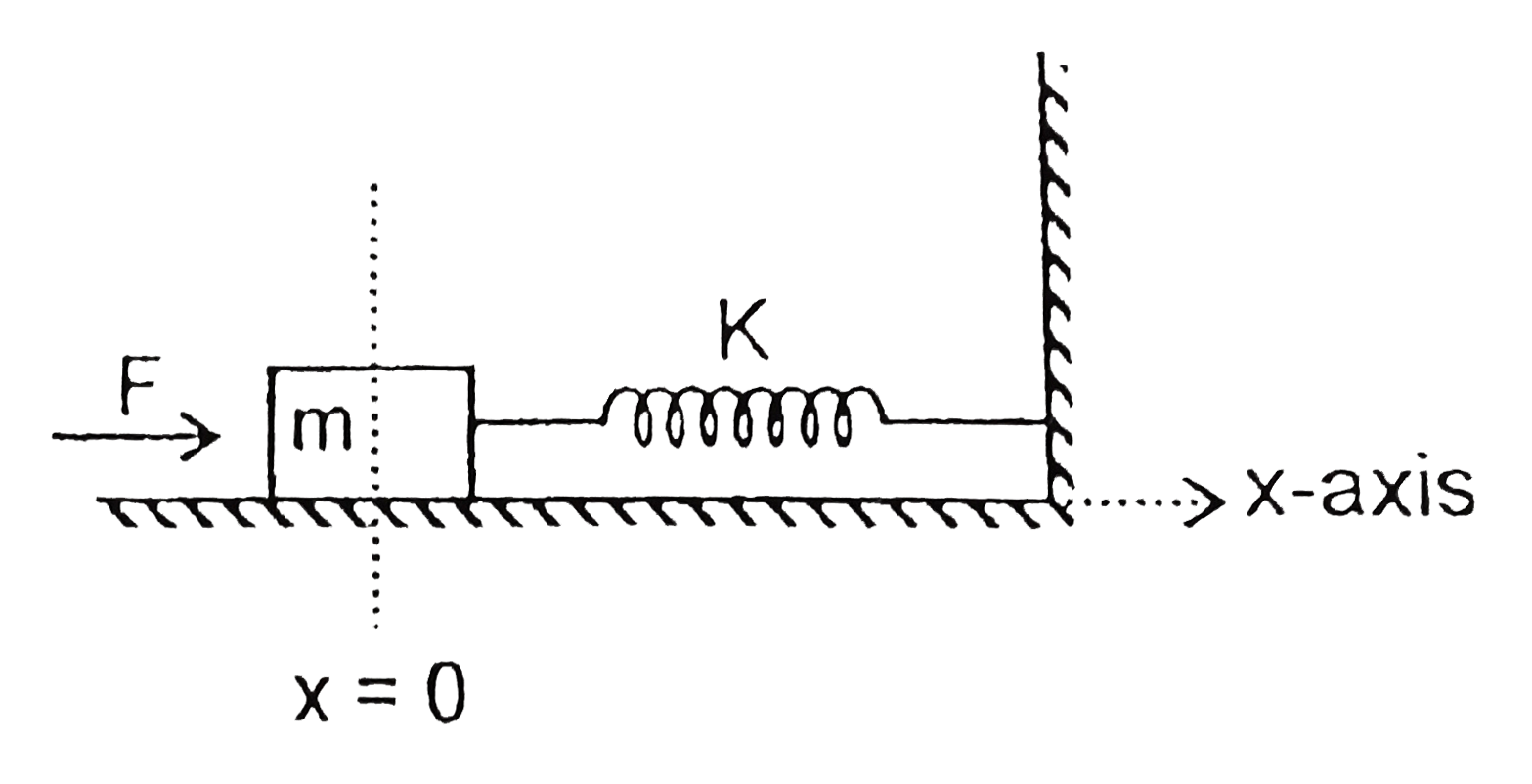
A block of mass m connected to a spring of stiffness k is placed on horizontal smooth surface. When block is at x=0, spring is in natural length. The block is also subjected to a force F=k|x|∘ thenAMotion of block is SHMBTime period of motion is π√mk[√2+√23]CTime period of motion is π√mk[1+√32]DSum of potential energy and kinetic energy of spring block system is maximum at right extreme.Two blocks A(3kg) and B(2kg) resting on a smooth horizontal surface is connected by a spring of stiffness 480N/m. Initially the spring is underformed and a velocity of 2m/s is imparted to A along the line of the spring away from B. The maximum extension in meters of the spring during subsequent motion is :-
A110B12√10C12√15D0.15
Two blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
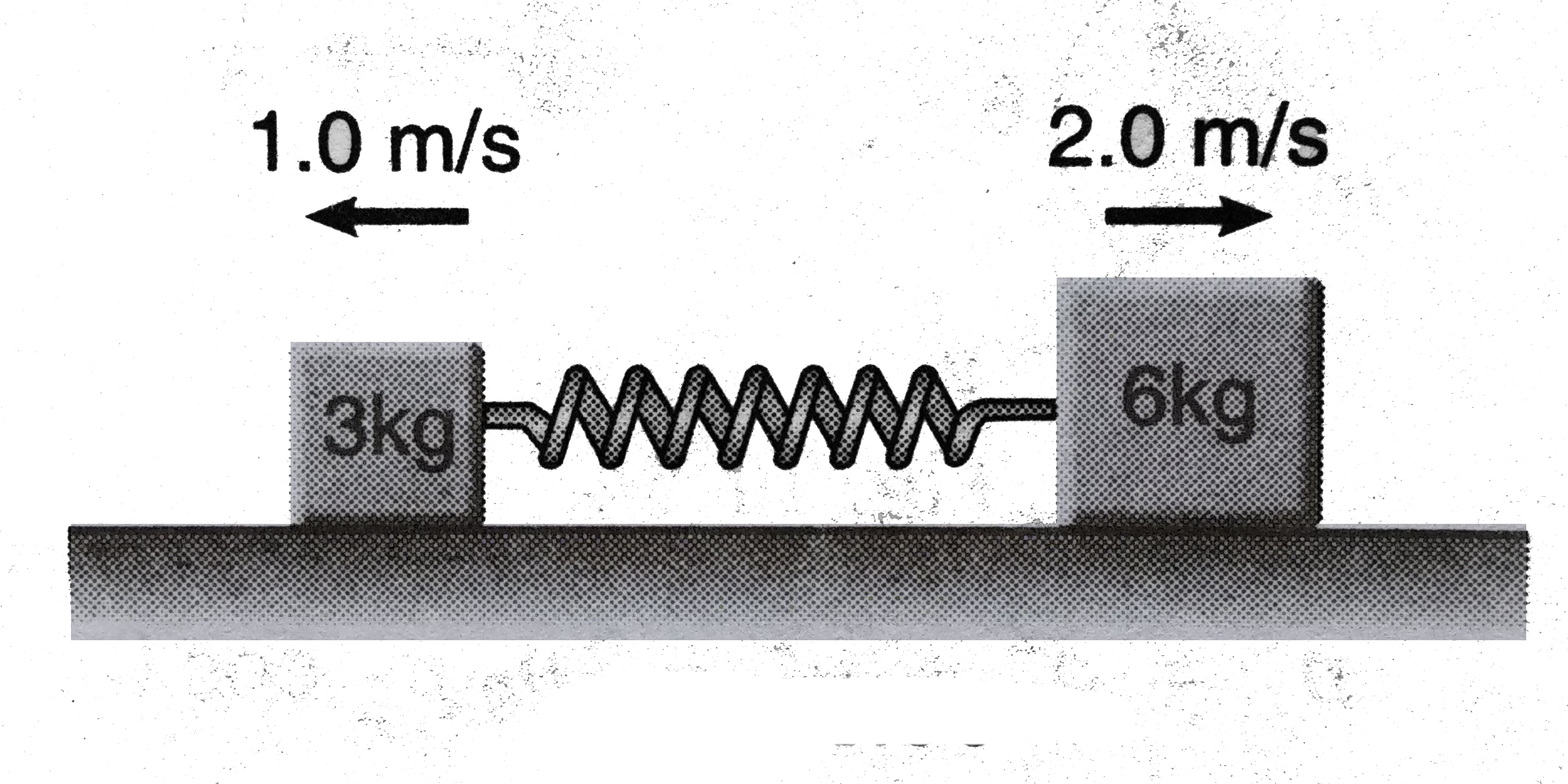
View SolutionTwo blocks of masses 3kg and 6kg respectivley are placed on a smooth horizontal surface. They are connected by a light spring of force constant k=200N/m. Initially the spring is unstretched. The indicated velocities are imparted to the blocks. Find the maximum extension of the spring.
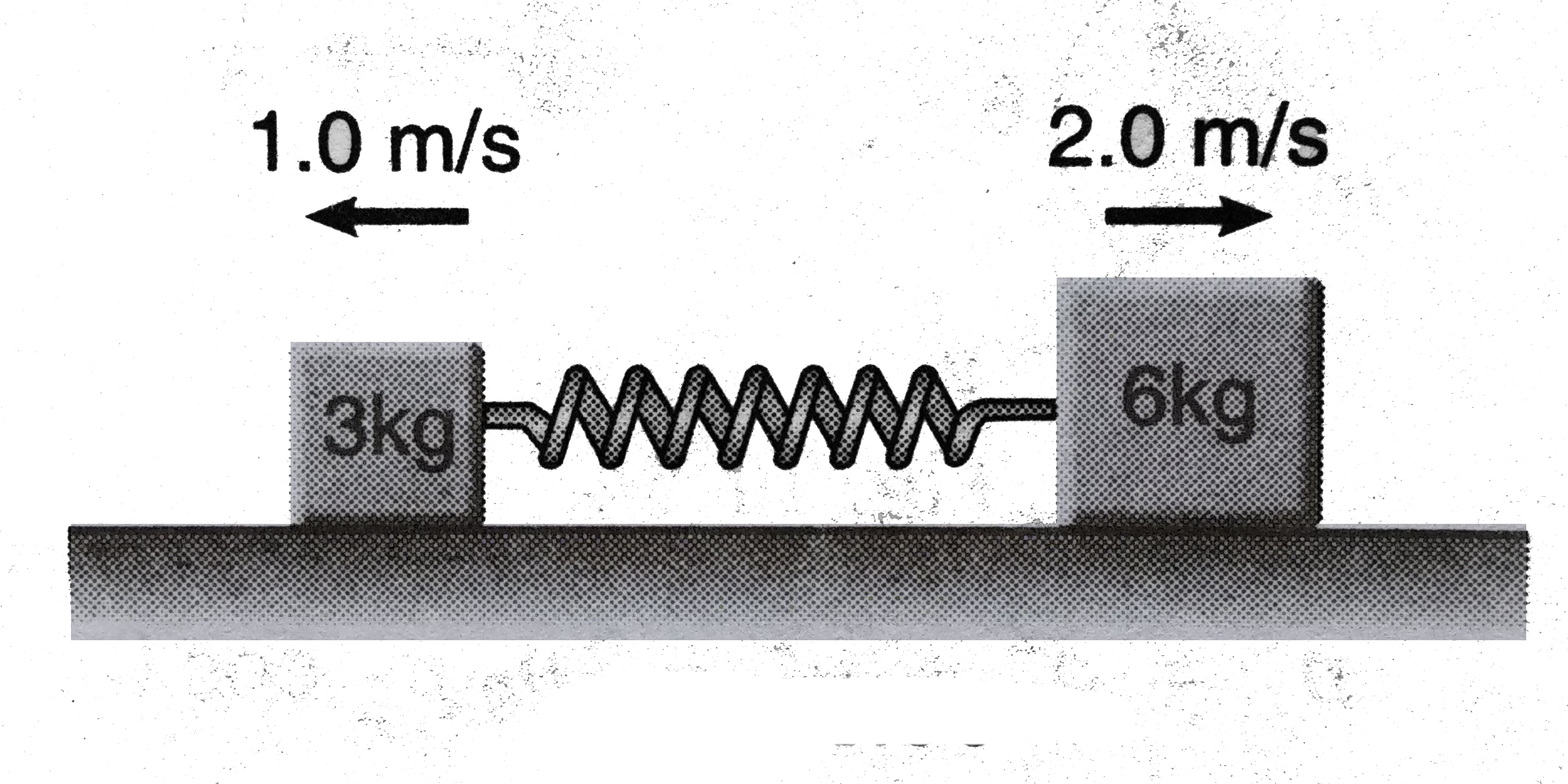
View SolutionA dumbbell consists of two balls A and B of mass m=1 kg and connected by a spring. The whole system is placed on a smooth horizontal surface as shown in the figure. Initially the spring is at its natural length, the ball B is imparted a velocity v0=8√7m/s in the direction shown. The spring constant of the spring is adjusted so that the length of the spring at maximum elongation is twice that of the natural, length of the spring. Find the maximum potential energy stored (in Joule) in the spring during the motion.

View SolutionA dumbbell consists of two balls A and B of mass m=1 kg and connected by a spring. The whole system is placed on a smooth horizontal surface as shown in the figure. Initially the spring is at its natural length, the ball B is imparted a velocity v0=8√7m/s in the direction shown. The spring constant of the spring is adjusted so that the length of the spring at maximum elongation is twice that of the natural, length of the spring. Find the maximum potential energy stored (in Joule) in the spring during the motion.

View SolutionTwo blocks of masses 7 kg and 3 kg are connected by a spring of stiffness 1000Nm−1 and placed on a smooth horizontal surface. They are acted by horizontal forces of 72 N and 32 N in opposite directions as shown in the figure. When accelerations of the blocks are equal and constant, the extension of the spring is
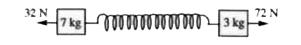
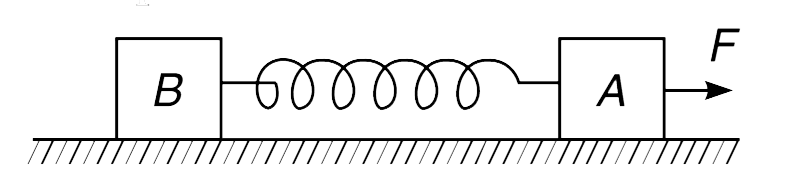
View SolutionTwo blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ?
View Solution
