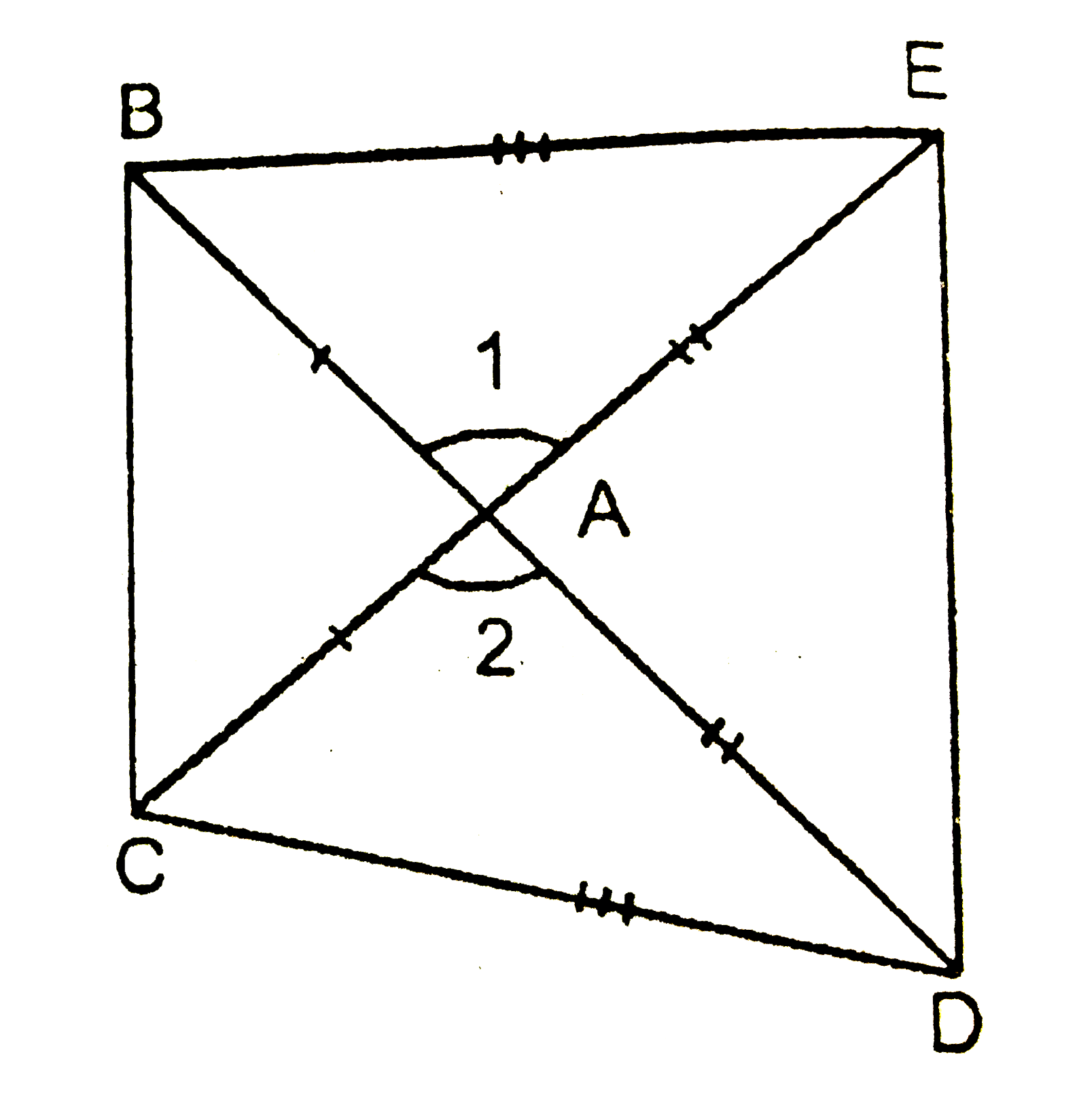
दिए गये चित्र में यदि . दिखायें कि .
(दिया हुआ है)
[CPCT]
[CPCT]
और [CPCT]
अब
इसी तरह से,
....(i)
अब और में,
और
[SAS समरूपता से]
Topper's Solved these Questions
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.1
22 Videos
- त्रिभुज BOOK - KC SINHACHAPTER - त्रिभुज EXERCISE - EXCERCISE 6.2 (अतिलघु उत्तरीय प्रश्न )
8 Videos
- त्रिकोणमितीय अनुपात और सर्वसमिकाएँ BOOK - KC SINHACHAPTER - त्रिकोणमितीय अनुपात और सर्वसमिकाएँ EXERCISE - EXERCISE 8.4
85 Videos
- दो चर वाले रैखिक समीकरण युग्मBOOK - KC SINHACHAPTER - दो चर वाले रैखिक समीकरण युग्मEXERCISE - वस्तुनिष्ठ प्रश्न
44 Videos
Similar Questions
कोष्ठक में दिए उपयुक्त शब्द से रिक्त स्थानों को भरें :
2 cm भुजा वाले सभी वर्ग ................. होते है । (सद्रश्य , सर्वागसम , सद्रश्य और सर्वागसम दोनों)
View SolutionΔABC में ,P और AB क्रमशः AB तथा AC पर दो बिन्दु इस प्रकार है कि PQ∣∣BC और APPB=23 तो AQQC का मान ज्ञात करें ।
View Solutionरिक्त स्थानों की पूर्ति करें :
sin2θ+cos2θ= ……………..
View Solutionयदि a1b2≠a2b1 तब समीकरण निकाय a1x+b1y+c1=0,a2x+b2y+c2=0 का
View SolutionIn ΔABC if AD is the altitude and O is the orthocentre of ΔABC then AO:OD=
View SolutionAD और PM त्रिभुजों ABC और PQR कि क्रमशः मध्यिकाएँ है जबकि ΔABC~ΔPQR है सिद्ध कीजिए कि ABPQ=ADPM है
View SolutionIn that figure, if ΔABE≅ΔACD, show that ΔADE≅ΔABC.
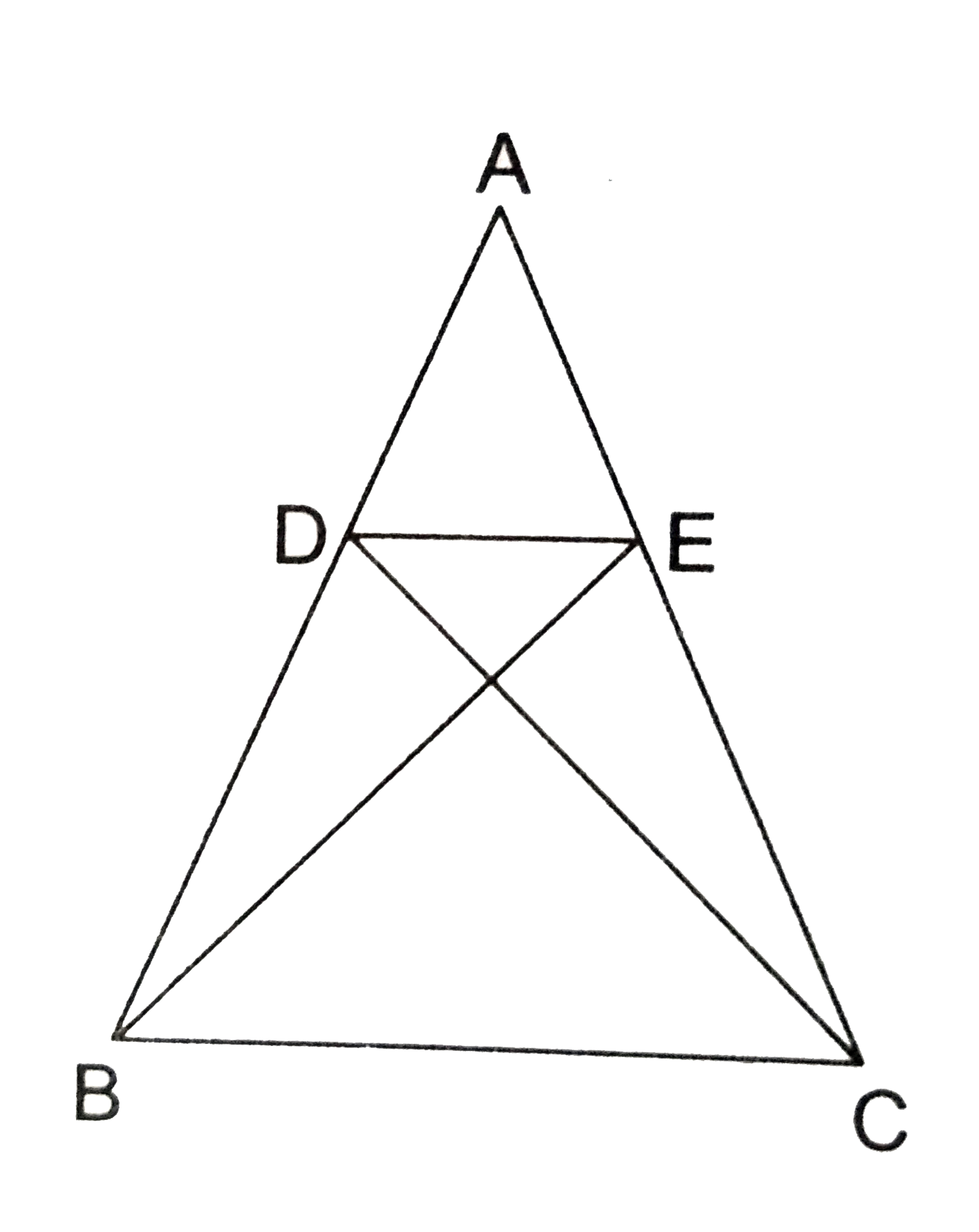
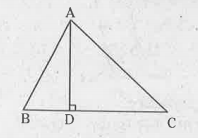
View SolutionΔABC में AD भुजा BC का लम्ब समद्विभाजक है। दर्शाइए कि ΔABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
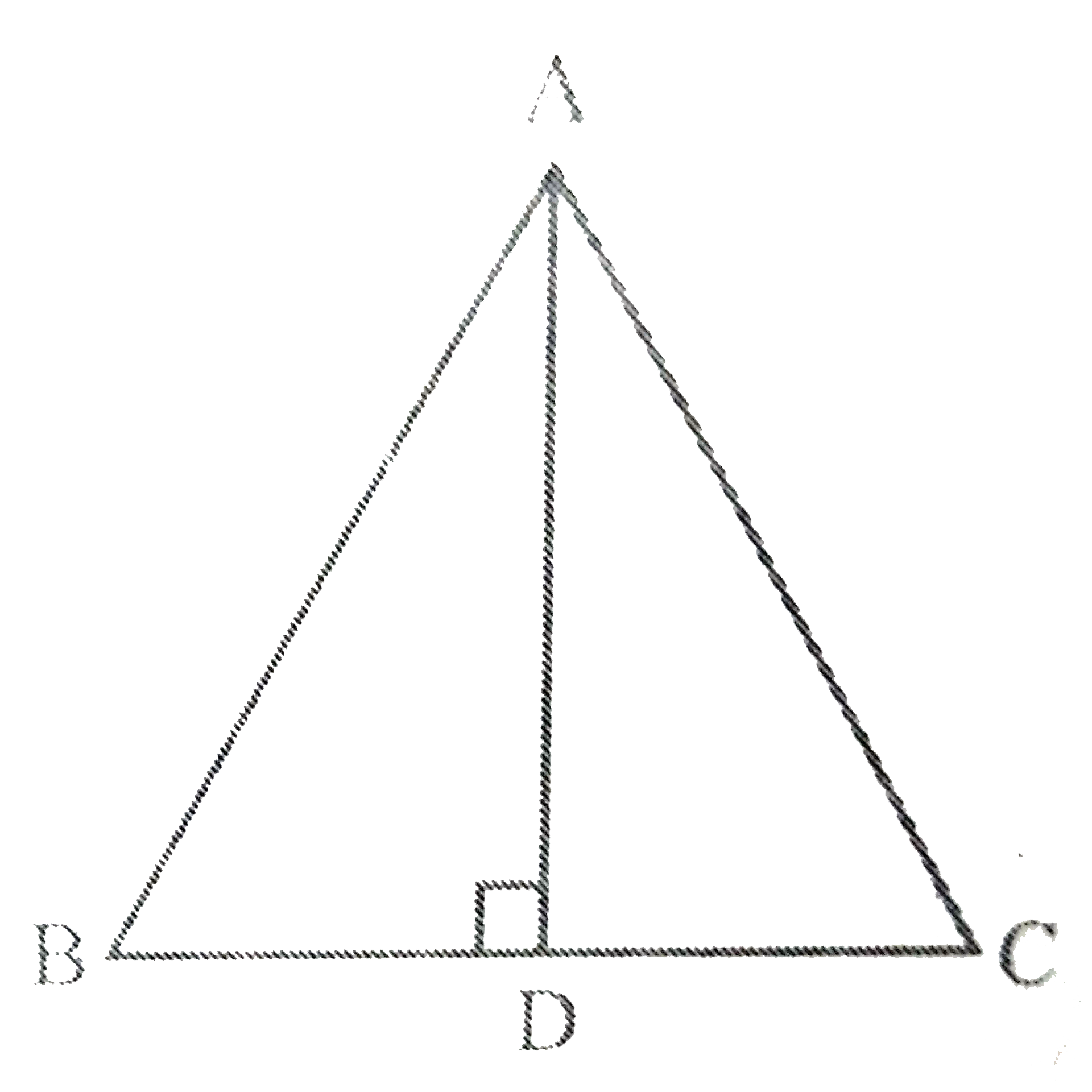
View SolutionΔABCमें ,AD,BC का लम्ब समद्विभाजक है तो दिखाइये कि ΔABC एक समद्विबाहु त्रिभुज है जिसमें AB = AC
View Solutionसमबाहु त्रिभुज ABC की AD एक ऊंचाई है|यदि AD को आधार लेकर एक समबाहु त्रिभुज ADE बनाई गई है तो सिद्ध करो की Area(ΔADE):Area(ΔABC)=3:4
View SolutionIf ΔABC be an equilateral triangle and AD⊥BC, then AD2 =
View SolutionIn Fig. If ΔABE=ACD , show that ΔADE~ΔABC .
View SolutionIn the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
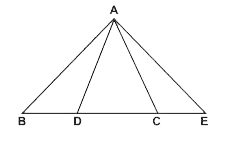
View SolutionΔABC లో AD⊥BC మరియు AD2=BD∗CD అయిన త్రిభుజము ABC లంబకోణ త్రిభుజామని చూపుము.
View SolutionAD, BE and CF are altitudes of △ ABC. If AD = BE = CF, prove that △ ABC is an equilateral triangle.
View Solution
