AD, BE and CF are altitudes of △ ABC. If AD = BE = CF, prove that △ ABC is an equilateral triangle.Solution in Gujrati
Step by step video & image solution for AD, BE and CF are altitudes of triangle ABC. If AD = BE = CF, prove that triangle ABC is an equilateral triangle. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - KUMAR PRAKASHANCHAPTER - TRIANGLESEXERCISE - MULTIPLE CHOICE QUESTIONS
15 Videos
- TRIANGLESBOOK - KUMAR PRAKASHANCHAPTER - TRIANGLESEXERCISE - SUMS TO ENRICH REMEMBER
9 Videos
- TRIANGLESBOOK - KUMAR PRAKASHANCHAPTER - TRIANGLESEXERCISE - EXERCISE 7.5
4 Videos
- SURFACE AREAS AND VOLUMESBOOK - KUMAR PRAKASHANCHAPTER - SURFACE AREAS AND VOLUMESEXERCISE - MULTIPLE CHOICE QUESTIONS
18 Videos
Similar Questions
In △ABC,∠A=∠C,AC=5 and BC = 4. Then, the perimeter of △ ABC is ..........
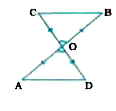
View SolutionIn the given figures, OA = OB and OD = OC. Show that
(i) △AOD=△BOC and (ii) AD||BC
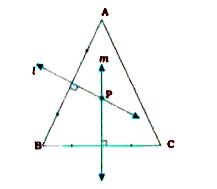
View SolutionABC is a triangle. Locate a point in the interior of △ ABC which is equidistant from all the vertices of △ ABC
View SolutionThe total surface area of a cuboid with length 20 cm, breadth 15 cm and height 10 cm is ……… cm2.
View SolutionAD BE and CF are the medians of a Delta ABC .Prove that 2(AD+BE+CF)<3(AB+BC+CA)<4(AD+BE+CF)
View SolutionIn given figure the altitudes AD, BE and CF , the altitudes of triangle ABC are equal. Prove that ABC is an equilateral triangle.
View SolutionIf in a Delta ABC,AD,BE and CF are the altitudes and R is the circumradius,then the radius of the circumcircle of Delta DEF is
View SolutionAD, BE and CF, the altitudes of ABC are equal. Prove that ABC is an equilateral triangle.
View SolutionAD, BE and CF, the altitudes of ABC are equal. Prove that ABC is an equilateral triangle.
View SolutionAD, एक समबाहु त्रिभुज ABC की एक ऊँचाई है | AD आधार का एक अन्य समबाहु त्रिभुज ADE यहाँ स्थित है | तो सिद्ध कीजिए कि (△ADE) का क्षेत्रफल : (△ABC) का क्षेत्रफल =3:4
View SolutionIf in a ΔABC,AD,BEandCF are the altitudes and R is the circumradius, then find the radius of the DEF.
View Solutionसमबाहु त्रिभुज ABC की AD एक ऊंचाई है|यदि AD को आधार लेकर एक समबाहु त्रिभुज ADE बनाई गई है तो सिद्ध करो की Area(ΔADE):Area(ΔABC)=3:4
View Solutionयदि AD, BE और CF एक त्रिभुज ABC कि मध्यिकाएँ है, तो सिद्ध करें कि −−→AD+−−→BE+−−→CF=→0
View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
View SolutionBE and CF are two equal altitudes of a triangle ABC. Using RHS congruence rule, prove that the triangle ABC is isosceles.
View Solution
