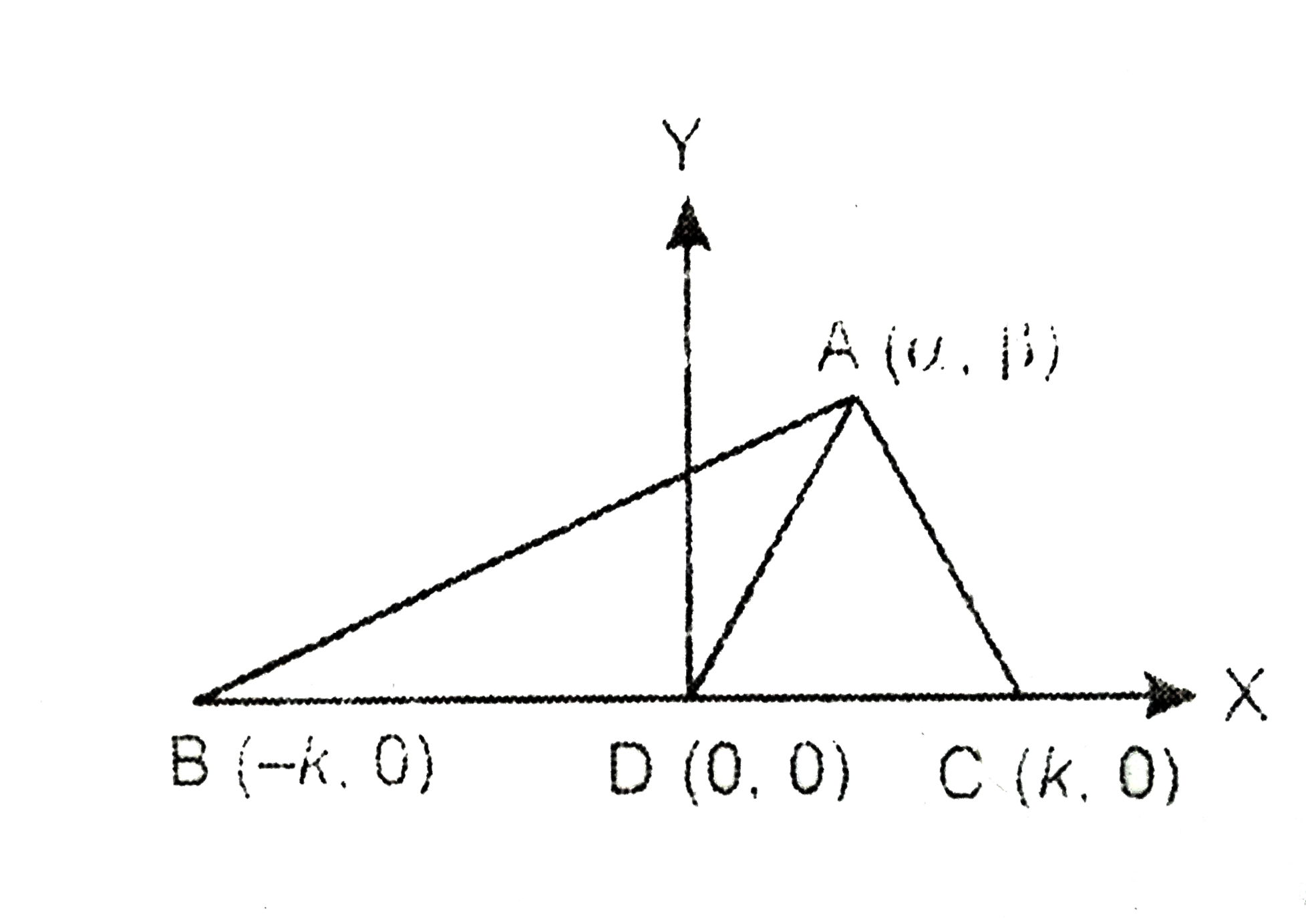
किसी ΔABC में सिध्द करे कि AB2+AC2=2(AD2+BD2), जहाँ D,BC का मध्य बिन्दु है |
हम D को मूल बिन्दु मान लेते है और DC तथा DY को क्रमश : x - अक्ष एव y - अक्ष है |
माना कि BC = 2k , तो B≡(−k,0),C≡(k,0)
मान ले A≡(α,β)
अब बाया पक्ष =AB2−AC2
=(α+k)2+(β−0)2+(α−k)2+(β+0)2
=α2+k2+2αk+β2+k2−2α+β2
=2α2+2β2+2k2=2(α2−β2+k2)
और दाया पक्ष = 2(AD2+BD2)
=2[(α−0)2+(β−0)2+(0−k)2+(0−0)2]
=2(α2−β2−k2)
अतः बाया पक्ष = दाया पक्ष
Topper's Solved these Questions
- निर्देशांक ज्यामिति BOOK - KC SINHACHAPTER - निर्देशांक ज्यामिति EXERCISE - प्रश्नावली 7.1 (अतिलघु उत्तरीय प्रश्न )
13 Videos
- निर्देशांक ज्यामिति BOOK - KC SINHACHAPTER - निर्देशांक ज्यामिति EXERCISE - प्रश्नावली 7.1 (लघु उत्तरीय प्रश्न )
5 Videos
- द्विघात समीकरण BOOK - KC SINHACHAPTER - द्विघात समीकरण EXERCISE - वस्तुनिष्ट प्रशन
37 Videos
- पृष्ठीय क्षेत्रफल और आयतन BOOK - KC SINHACHAPTER - पृष्ठीय क्षेत्रफल और आयतन EXERCISE - वस्तुनिष्ट प्रश्न(Objective Questions)
30 Videos
Similar Questions
निम्नलिखित बिन्दुए किस चतुर्थेाश में स्थित है |
(10,−3)
View Solutionयदि किसी आयत के तीन शीर्ष (−2,0),(2,0),(2,1) है तो चौथे शीर्ष के नियामक ज्ञात कीजिए |
View Solutionयदि a और b समीकरण x2−ax+b=0 के मूल है तब
View Solutionएक खोखला धातुई गोला जिसकी बाह्य त्रिज्या 6cm और अन्तः त्रिज्या 4cm है को पिघलाया जाता है और इसे एक शंकु जिसके आधार की त्रिज्या 6cm है, के रूप में ढाला जाता है, तो शंकु की ऊँचाई है:
View SolutionIf ABC is an isosceles triangle and D is a point on BC such that AD⊥BC , then AB2−AD2=BD.DC (b) AB2−AD2=BD2−DC2 (c) AB2+AD2=BD.DC (d) AB2+AD2=BD2−DC2
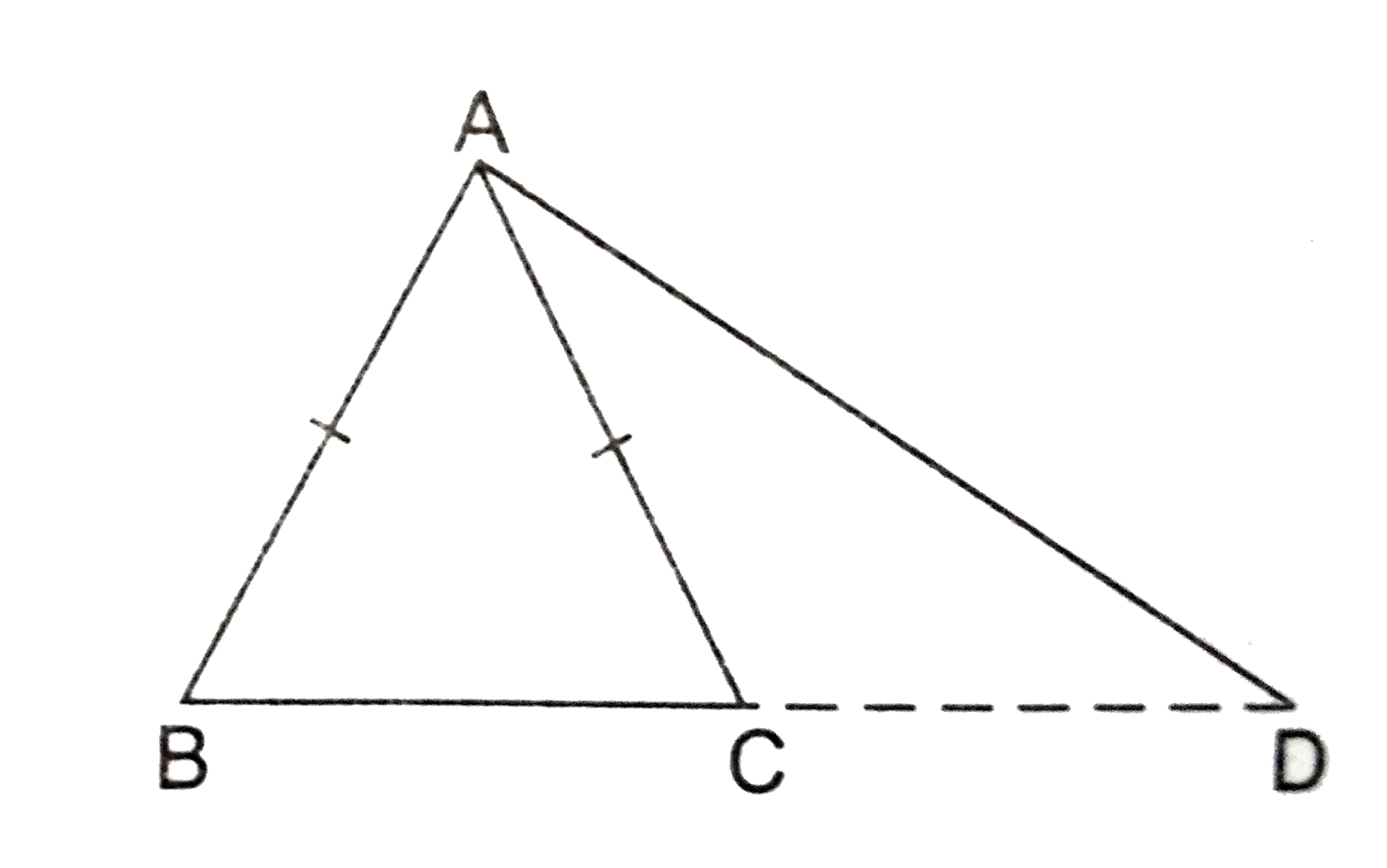
View SolutionIn an isoscles ΔABC,AB=ACandD is a point on BC. Prove that AB2−AD2=BD⋅CD.
View SolutionIn ΔABC,AB=AC. Side BC is produced to D. Prove that (AD2−AC2)=BD⋅CD.
View Solutionयदि ΔABC की भुजा BC का मध्य बिन्दु D है तब सिद्ध कीजिये कि
AB2+AC2=2(AD2+BD2)
View Solutionएक त्रिभुज ABC है | जिसमे AB = AC तथा D, BC पर कोई बिंदु है | तो सिद्ध कीजिए कि
AB2−AD2=BD⋅CD
View Solutionसिद्ध कीजिए कि:
∣∣∣ad+bcbd−acac−bdad+bc∣∣∣=(a2+b2)(c2+d2).
View SolutionIf in ΔABC,AD⊥BC,then prove that AB2+CD2=AC2+BD2
View Solutionसमकोण ΔABC में ∠A=90∘ तथा AD भुजा BC पर लम्ब है सिद्ध कीजिये कि
AB2−BD2=AC2−CD2
View Solutionसिद्ध कीजिए कि: ∣∣∣ad+bcac−bdbd−acad+bc∣∣∣=(a2+b2)(c2+d2)
View Solutionयदि ΔABC में AD|BC है, तो सिद्ध करें कि AB2 +CD2 =BD2+AC2.
View SolutionIn ΔABC, BD:CD=3:1 and AD⊥BC. Prove that 2(AB2−AC2)=BC2.
View Solution
