If ABC is an isosceles triangle and D is a point on BC such that AD⊥BC , then AB2−AD2=BD.DC (b) AB2−AD2=BD2−DC2 (c) AB2+AD2=BD.DC (d) AB2+AD2=BD2−DC2
Step by step video & image solution for If A B C is an isosceles triangle and D is a point on B C such that A D_|_B C , then A B^2-A D^2=B DdotD C (b) A B^2-A D^2=B D^2-D C^2 (c) A B^2+A D^2=B DdotD C (d) A B^2+A D^2=B D^2-D C^2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In an equilateral triangle ABC if AD⊥BC, then AD2 = (a)CD2 (b) 2CD2 (c) 3CD2 (d) 4CD2
View SolutionABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
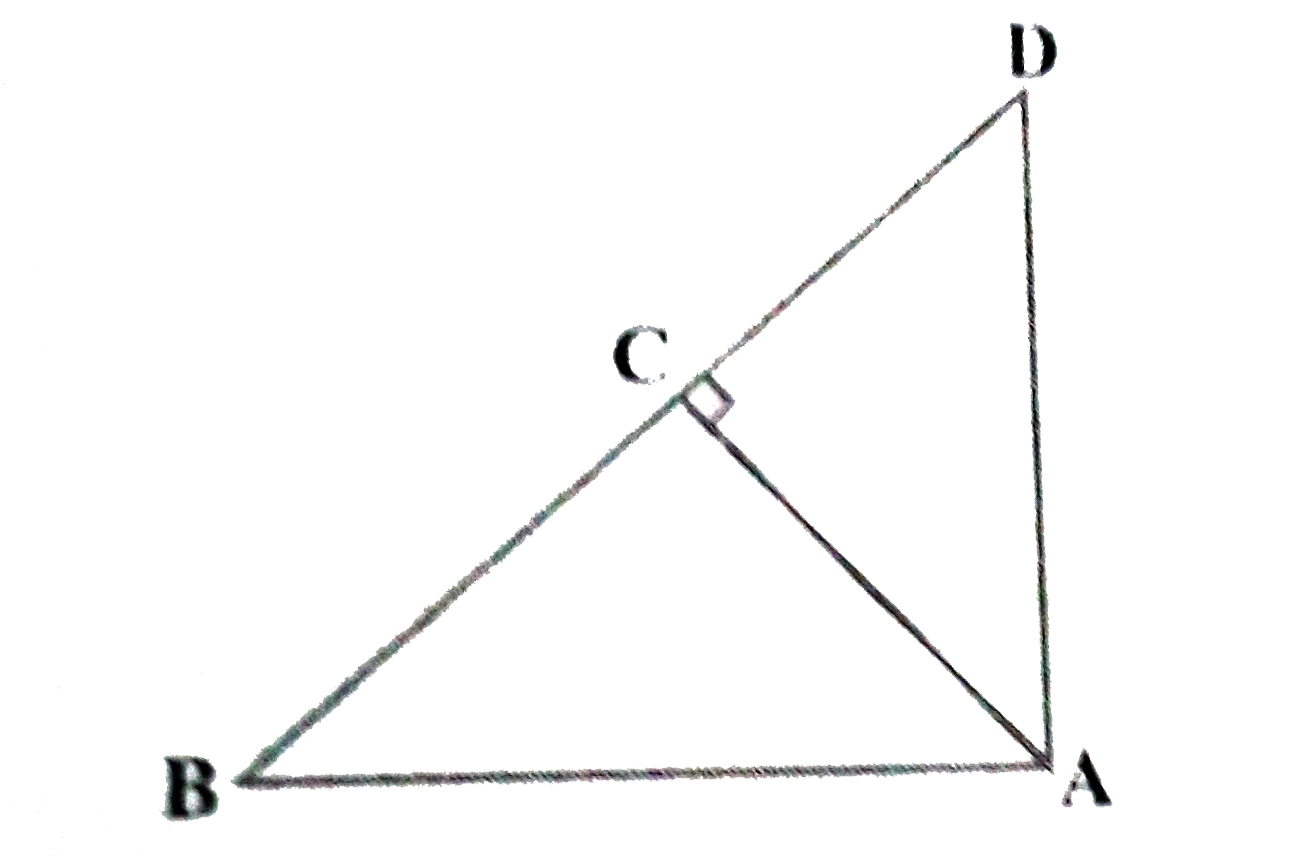
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn figure, O is a point in the interior of a triangle ABC, OD⊥BC,OE⊥ACand OF⊥AB. Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AW2+CD2+BF2

View SolutionIn A B C, if AB=10,BC=8,CA=12 and a point D is taken on AB such that A D: D B is 3:2 , then the square of length of CD is
View SolutionIn ABC , AD is a median. Prove that AB2+AC2=2 AD2+2 DC2 .
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
View SolutionIn a scalene triangle ABC,D is a point on the side AB such that CD2=ADDB, sin s∈AS∈B=sin2C2 then prove that CD is internal bisector of ∠C.
View SolutionA point D is taken on the side BC of a ABC such that BD=2dC. Prove that ar(ABD)=2ar(ADC).
View Solution
