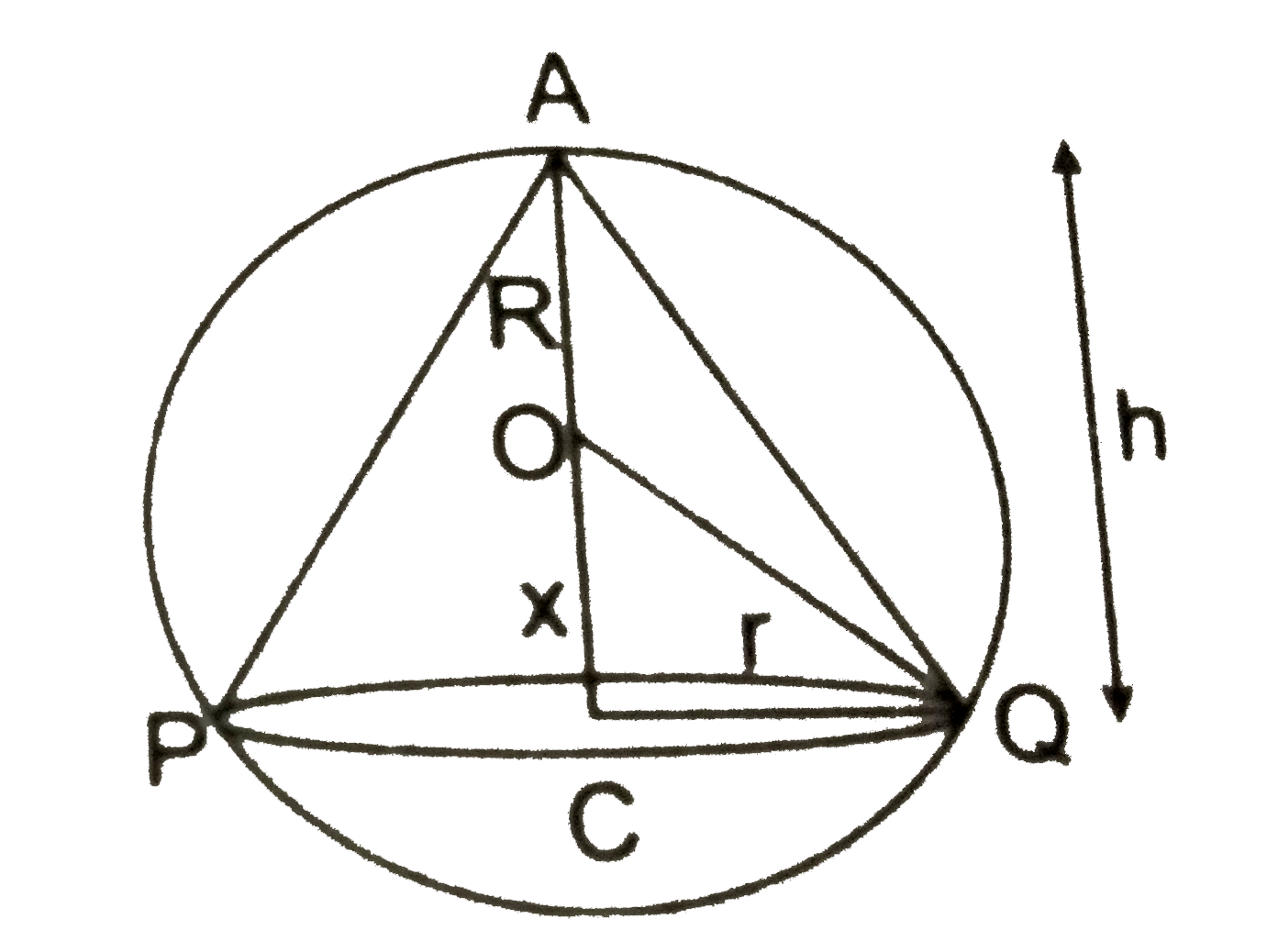
सिद्ध कीजिए कि R त्रिज्या के गोले के अन्तर्गत विशालतम शंकु का आयतन, गोले कि आयतन का $\frac{8}{27}$ होता है.

Video Solution

Text Solution

Verified by Experts

मान लीजिए कि $O C = x, C Q = r$
अब $O A = R$ (दिया है)
शंकु कि ऊँचाई $= h = x + R ... (1)$
$∴$ शंकु का आयतन $= V = \frac{1}{3} π r^{2} h$
अब समकोण $Δ O C Q$ में, $O C^{2} + C Q^{2} = O Q^{2}$
$\Rightarrow x^{2} + r^{2} = R^{2}$
$\Rightarrow r^{2} = R^{2} - x^{2} ... (2)$
समीकरण (1 ) और (2 ) से h और r का मान V में रखने पर,
$V = \frac{1}{3} π (R^{2} - x^{2}) (x + R) [∵ h = x + R] ... (3)$
समीकरण (3 ) को x के सापेक्ष अवकलन करने पर,
$\frac{d V}{d x} = \frac{1}{3} π [(R^{2} - x^{2}) - 2 x (x + R)]$
$\Rightarrow \frac{d V}{d x} = \frac{π}{3} [R^{2} - x^{2} - 2 x^{2} - 2 x R]$
$\Rightarrow \frac{d V}{d x} = \frac{π}{3} (R^{2} - 2 x R - 3 x^{2})$
$\Rightarrow \frac{d V}{d x} = \frac{π}{3} (R - 3 x) (R + x) ... (4)$

उच्चतम मान के लिए $\frac{d V}{d x} = 0$
$\frac{π}{3} (R - 3 x) (R + x) = 0$
$\Rightarrow x = \frac{R}{3}$ या $x = - R \Rightarrow x = \frac{R}{3}$
$(∵ x$ त्राणात्मक नहीं हो सकता है)
x के सापेक्ष समीकरण (4 ) का अवकलन करने पर,
$\frac{d^{2} V}{{d x}^{2}} = \frac{π}{3} [(- 3) (R + x) + (R - 6 x)$
$x = \frac{R}{3}$ पर, $\frac{d^{2} V}{{d x}^{2}} = \frac{- π}{3} (2 R + \frac{6 R}{3}) = - \frac{4 π}{3} R < 0$
$∴ V$ का स्थानीय उच्चतम मान $x = \frac{R}{3}$ पर है
अब x का मान समीकरण (3 ) में रखने पर,
$V = \frac{π}{3} (R^{2} - \frac{R^{2}}{9}) (R + \frac{R}{3})$
$= \frac{π}{3} . \frac{8 R^{2}}{9} . \frac{4 R}{3} = \frac{8}{27} (\frac{4}{3} π R^{3})$
$\Rightarrow V = \frac{8}{27} \times$ गोले का आयतन

Updated on:21/07/2023

|

Class 12 MATHS INTEGRALS

Topper's Solved these Questions

Similar Questions

NOOTAN HINDI-अवकलन के अनुप्रयोग -प्रश्नावली 6.5

Home
Ask Doubt
Profile