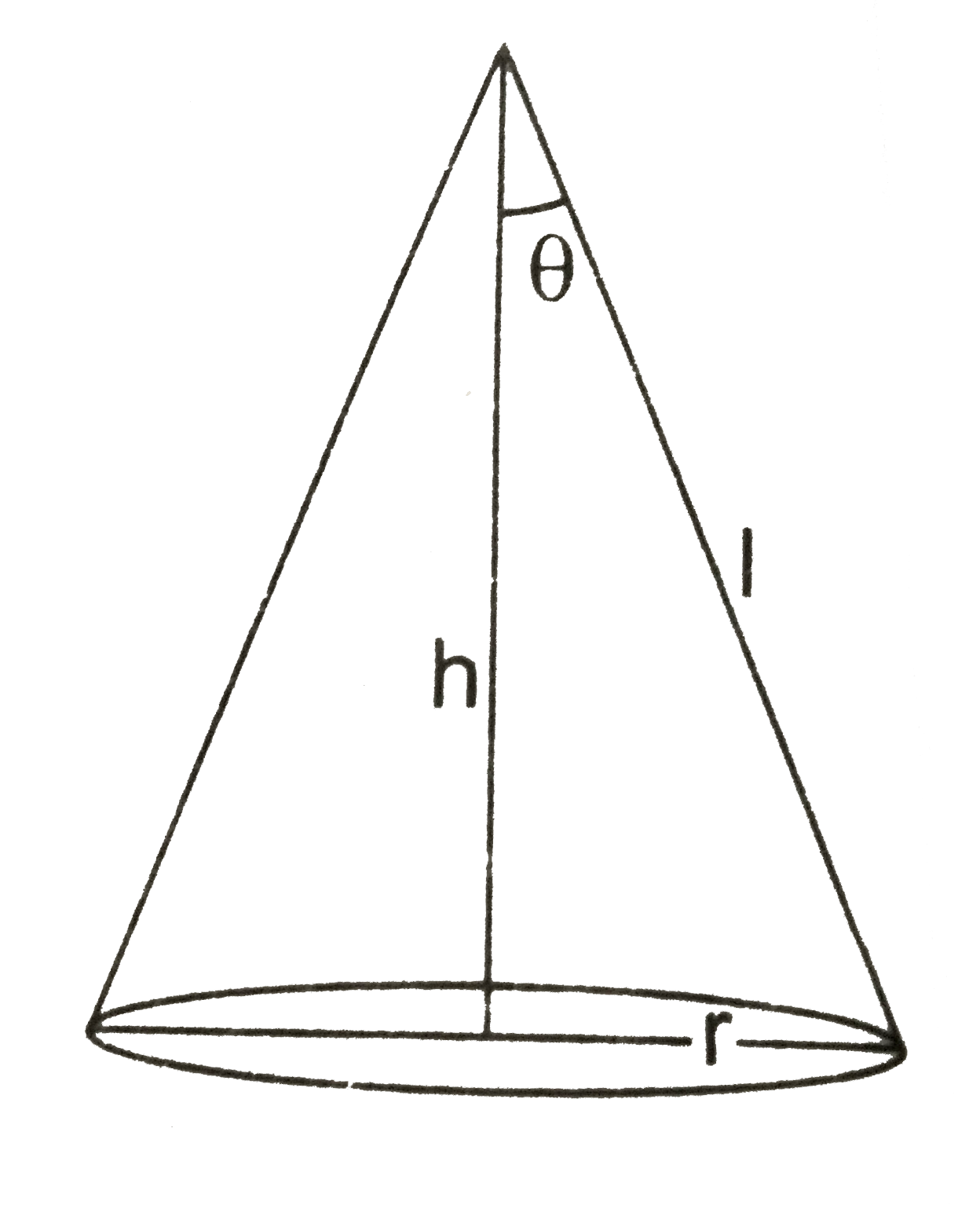
सिद्ध कीजिए कि दी गई तिर्यक ऊँचाई और महत्तम आयतन वाले शंकु का अर्द्धशीर्ष ${tan}^{- 1} \sqrt{2}$ होता है.

Video Solution

Text Solution

Verified by Experts

माना शंकु के आधार कि त्रिज्या 'r ' और ऊँचाई 'h ' है
$∴ h^{2} + r^{2} + l^{2}$ जहाँ l दी गई तिर्यक ऊँचाई है.
$\Rightarrow r^{2} = l^{2} - h^{2} ... (1)$
शंकु का आयतन $V = \frac{1}{3} π r^{2} h$
$\Rightarrow V = \frac{1}{3} π h (l^{2} - h^{2})$
$= \frac{1}{3} π (l^{2} h - h^{2})$
$\Rightarrow \frac{d V}{d h} = \frac{1}{3} π (l^{2} - 3 h^{2})$

उच्चिष्ट/निम्निष्ठ के लिये, $\frac{d V}{d h} = 0$
$\Rightarrow l^{2} - 3 h^{2} = 0$
$\Rightarrow l^{2} = 3 h^{2}$
और $\frac{d^{2} V}{d h^{2}} = \frac{1}{3} π (0 - 6 h) = - 2 π h < 0$
$\Rightarrow V$ उच्छिष्ट है
अब समीकरण (2 ) से
$l^{2} = 3 h^{2}$
$\Rightarrow r^{2} + h^{2} = 3 h^{2}$ [समीकरण (1 ) से]
$\Rightarrow r^{2} = 2 h^{2}$
$\Rightarrow r = \sqrt{2} \cdot h \Rightarrow \frac{r}{h} = \sqrt{2}$
$\Rightarrow tan θ = \sqrt{2}$ यहाँ $θ$ शंकु का अर्द्धशीर्ष कोण है.
$\Rightarrow θ = {tan}^{- 1} \sqrt{2}$
अतः उच्चतम आयतन वाले शंकु का अर्द्धशीर्ष कोण ${tan}^{- 1} \sqrt{2}$

Updated on:21/07/2023

|

Class 12 MATHS INTEGRALS

Topper's Solved these Questions

Similar Questions

NOOTAN HINDI-अवकलन के अनुप्रयोग -प्रश्नावली 6.5

Home
Ask Doubt
Profile