सिद्ध कीजिए कि दिए हुआ पृष्ठ और महत्तम आयतन वाले लम्ब वृत्तीय शंकु का अर्ध शीर्ष कोण ${sin}^{- 1} (\frac{1}{3})$ होता है.

Video Solution

Text Solution

Verified by Experts

माना शंक्वाकार डेरे कि त्रिज्या 'r ' और ऊँचाई 'h ' है. यदि तिर्यक कि ऊँचाई 'l ' है,
इसका सम्पूर्ण पृष्ठ
$S = π r^{2} + π r l$
$\Rightarrow l = \frac{S - π r^{2}}{π r}$
शंकु का आयतन $V = \frac{1}{3} π^{2} r^{4} h^{2}$
$\Rightarrow V^{2} = \frac{1}{9} π^{2} r^{4} h^{2}$

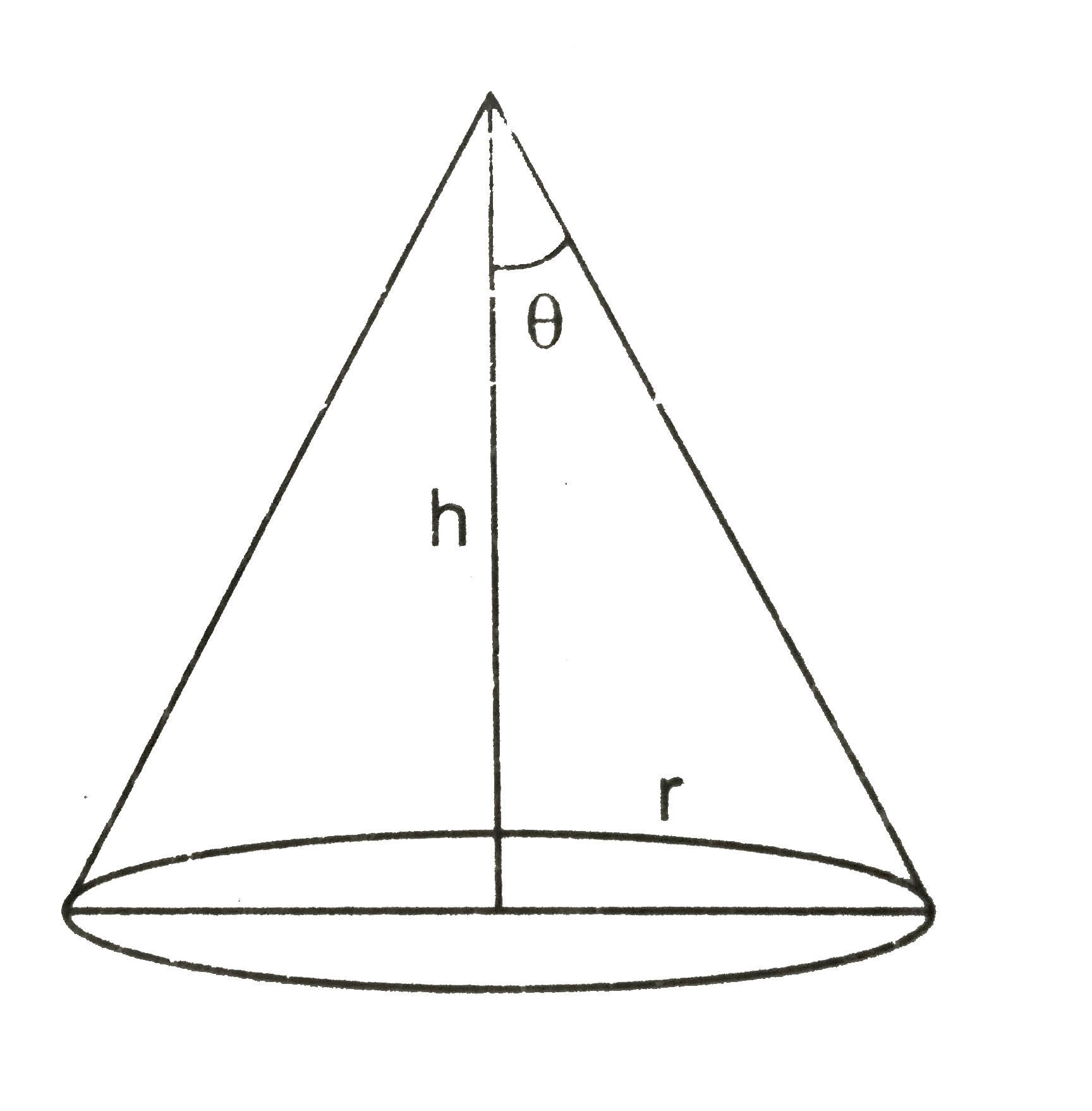
$V^{2} = \frac{1}{9} π^{2} r^{4} (l^{2} - r^{2})$
$= \frac{1}{9} π^{2} r^{4} [{(\frac{S - π r^{2}}{π r})}^{2} - r^{2}]$
$= \frac{1}{9} π^{2} r^{4} ⎡ ⎣ \frac{{(S - π r^{2})}^{2} - π^{2} r^{4}}{π^{2} r^{2}} ⎤ ⎦$
$\Rightarrow = \frac{1}{9} r^{2} [S^{2} - 2 π S r^{2}]$
माना $Z = V^{2} = \frac{S}{9} [S r^{2} - 2 π r^{4}]$
$\frac{d Z}{d r} = \frac{S}{9} [2 S r - 8 π r^{3}]$
अब $\frac{d^{2} Z}{d r^{2}} = \frac{S}{9} (2 S - 24 π r^{2})$
उच्चिष्ठ/नमनिष्ठ के लिये $\frac{d Z}{d r} = 0$
$\Rightarrow 2 S r = 8 π r^{3}$
$\Rightarrow 2 (π r^{2} + π r l) = 8 π r^{2}$
$\Rightarrow π r l = 3 π r^{2}$
$\Rightarrow l = 3 r \Rightarrow \frac{r}{l} = \frac{1}{3}$
$\Rightarrow sin α = \frac{1}{3}$ जहाँ $α =$ अर्द्धशिर्ष कोण है.
$α = {sin}^{- 1} \frac{1}{3}$
$l = 3 r$ पर
$\frac{d^{2} Z}{d r^{2}} = \frac{S}{9} (2 S - 24 π r^{2})$
$= \frac{2 S}{9} (π r^{2} + π r l - 12 π r^{2})$
$= π r \frac{2 S}{9} (1 - 11 r)$
$= \frac{2 S π r}{9} (- 8 r) < 0$
अतः Z अधिकतम है.
$\Rightarrow V^{2}$ अधिकतम है
$\Rightarrow V$ अधिकतम है.
अतः अधिकतम आयतन के लिये अर्द्धशिर्ष कोण $= {sin}^{- 1} \frac{1}{3}$

Updated on:21/07/2023

|

Class 12 MATHS INTEGRALS

Topper's Solved these Questions

Similar Questions

NOOTAN HINDI-अवकलन के अनुप्रयोग -प्रश्नावली 6.5

Home
Ask Doubt
Profile