Prove that 3OD+DA+DB+DC is equal to OA+OB+OC.
To prove that 3OD+DA+DB+DC=OA+OB+OC, we will use the concept of position vectors. Let's denote the position vectors as follows:
- Let the position vector of point O be →O=→0 (the origin).
- Let the position vector of point D be →D.
- Let the position vector of point A be →A.
- Let the position vector of point B be →B.
- Let the position vector of point C be →C.
Step 1: Express the vectors in terms of position vectors
We can express the vectors OD, DA, DB, and DC in terms of the position vectors:
1. Vector OD:
→OD=→D−→O=→D−→0=→D
2. Vector DA:
→DA=→A−→D
3. Vector DB:
→DB=→B−→D
4. Vector DC:
→DC=→C−→D
Step 2: Substitute the vectors into the equation
Now we substitute these expressions into the left-hand side of the equation 3OD+DA+DB+DC:
3→OD+→DA+→DB+→DC=3→D+(→A−→D)+(→B−→D)+(→C−→D)
Step 3: Simplify the expression
Now we simplify the expression:
=3→D+→A−→D+→B−→D+→C−→D
=(3→D−→D−→D−→D)+→A+→B+→C
=→A+→B+→C
Step 4: Compare with the right-hand side
The right-hand side of the equation is:
→OA+→OB+→OC=→A+→B+→C
Conclusion
Since both sides of the equation are equal, we have:
3OD+DA+DB+DC=OA+OB+OC
Thus, we have proved the statement.
- Let the position vector of point D be →D.
- Let the position vector of point A be →A.
- Let the position vector of point B be →B.
- Let the position vector of point C be →C.
We can express the vectors OD, DA, DB, and DC in terms of the position vectors:
→OD=→D−→O=→D−→0=→D
→DA=→A−→D
→DB=→B−→D
→DC=→C−→D
Now we substitute these expressions into the left-hand side of the equation 3OD+DA+DB+DC:
3→OD+→DA+→DB+→DC=3→D+(→A−→D)+(→B−→D)+(→C−→D)
Now we simplify the expression:
=3→D+→A−→D+→B−→D+→C−→D
=(3→D−→D−→D−→D)+→A+→B+→C
=→A+→B+→C
The right-hand side of the equation is:
→OA+→OB+→OC=→A+→B+→C
Since both sides of the equation are equal, we have:
3OD+DA+DB+DC=OA+OB+OC
Thus, we have proved the statement.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 3
11 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Single Option Correct Type Questions)
81 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 1
7 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
Knowledge Check
A point O lies inside a square ABCD such that OA=3, OB=4 and OD=5, find the value of OC.
AA)3√3BB)6.67CC)3√2DD)4√2In the given figure, rays OA, OB, OC and OD are such that ∠AOB = 50∘ , ∠BOC = 90∘, ∠COD=70∘ and ∠AOD=x∘. Then, the value of x is
 A50∘B70∘C150∘D90∘
A50∘B70∘C150∘D90∘OA, OB, OC are the sides of a rectangular parallelopiped whose diagonals are OO', AA' , BB' and CC' . D is the centre of the rectangle AC'O'B' and D' is the centre of the rectangle O'A'CB' . If the sides OA, OB , OC are in the ratio 1:2:3 , the angle∠DOD' is equal to
Acos−1(24)√697Bcos−1(22)√619Csin−1(24)√697Dsin−1(22)√619
Suppose line segments AB and CD intersect at O in such a way that AO=OD and OB=OC. Prove that AC=BD but AC may not be parallel to BD
View SolutionIf a plane cuts off intercepts OA=a,OB=b,OC=c from the coordinate axes 9where 'O' is the origin). then the area of the triangle ABC is equal to
View SolutionIn the figure shown, OABC is a rectangle with OA=3 units, OC = 4 units. If BD = 2.5 units, then the slope of the diagonal OB is equal to
View SolutionOAOC=ODOB. Prove that ∠A=∠C and ∠B=∠D.
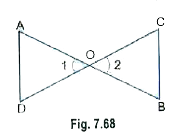
View SolutionIf ABCD is a rombus whose diagonals cut at the origin O, then OA + OB + OC + OD equals to
View Solution
