A line passes through the points whose position vectors are ˆi+ˆj−2ˆk and ˆi−3ˆj+ˆk. The position vector of a point on it at unit distance from the first point is
15(5ˆi+ˆj−7ˆk)
15(4ˆi+9ˆj−15ˆk)
(ˆi−4ˆj+3ˆk)
15(ˆi−4ˆj+3ˆk)
The correct Answer is:A
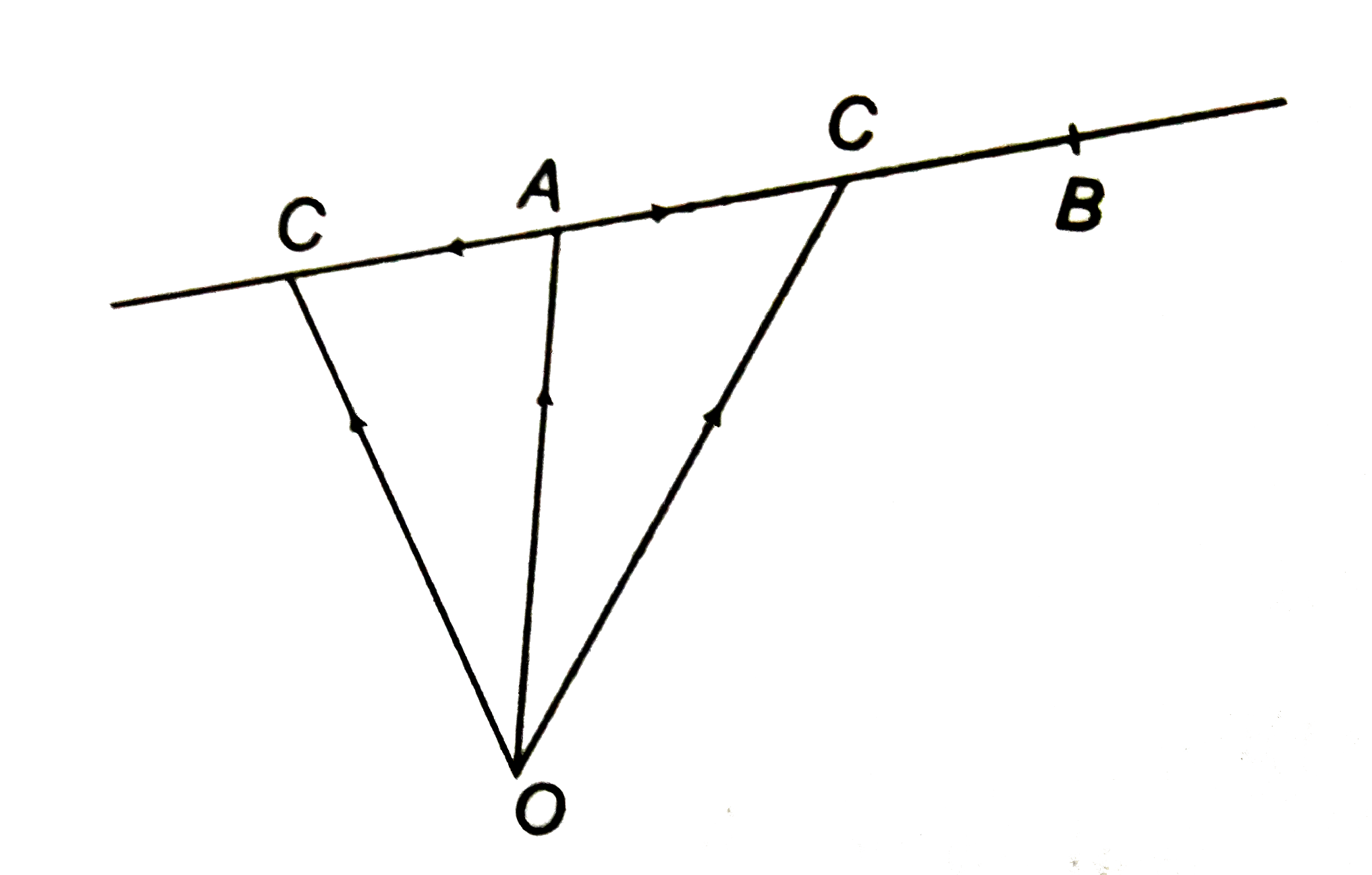
We have, A(ˆi+ˆj−2ˆk)andB(ˆi−3ˆj+ˆk).
On line AB points C and C' are at distance 1 unit from A.
OC=OA+AC, where AC is unit vector in direction of AB
∴OC=OA+AB|AB|
Similarly, OC'=OA−AB|AB|
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (More Than One Correct Option Type Questions)
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Statement I And Ii Type Questions)
3 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 3
11 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
A linepasses through the points whose positions vectors ˆi+ˆj−2ˆk and ˆi−3ˆj+ˆk. The position vector of a point on it at a unit distance from the first point is (A) ˆi−ˆj+3ˆjk (B) 15(4ˆi+9ˆj−13ˆk0 (C) 15(6ˆi+ˆj−7ˆk) (D) none of these
View SolutionFind the equation of a line passes through the points whose position vectors are (ˆi+4ˆj+ˆk) and (2ˆi−ˆj+5ˆk).
View Solution
Knowledge Check
The position vectors of A and B are ˆi−ˆj+2ˆkand3ˆi−ˆj+3ˆk. The position vector of the middle points of the line AB is
A12ˆi−12ˆj+ˆkB2ˆi−ˆj+52ˆkC32ˆi−12ˆj+32ˆkDnone of theseThe points with position vectors 5ˆi+5ˆk,−4ˆi+3ˆj−ˆk and 2ˆi+ˆj+3ˆk
AcollinearBnon-collinearCnon-collinear and non planarDnon-collinear but coplanarIf the point whose position vectors are 2ˆi+ˆj+ˆk,6ˆi−ˆj+2ˆkand12ˆi−5ˆj+pˆk are collinear, then the value of p is
A2B4C6D8
Show that the three points whose position vectors are −3ˆi+ˆj+5ˆk,2ˆi+3ˆk,−13ˆi+3ˆj+9ˆk are collinear
View SolutionFind the vector equation of a lin e passes through the point whose position vector is (2ˆi−ˆj−ˆk) and parallel to vector ˆi+5ˆk.
View SolutionShow that the points with position vectors ˆi+2ˆj+7ˆk,2ˆi+6ˆj+3ˆk and 3ˆi+10ˆj−ˆk are collinear
View SolutionIf the point whose position vectors are 2ˆi+ˆj+ˆk,6ˆi−ˆj+2ˆkand12ˆi−5ˆj+pˆk are collinear, then the value of p is
View SolutionA unit vector perpendicular to the plane passing through the points whose position vectors are ˆi−ˆj+2ˆk,2ˆi−ˆk and 2ˆi+ˆk is
View Solution
