If in a triangle AB=a,AC=b and D,E are the mid-points of AB and AC respectively, then DE is equal to
a4−b4
a2−b2
b4−a4
b2−a2
The correct Answer is:D
To solve the problem, we need to find the length of segment DE in triangle ABC, where D and E are the midpoints of sides AB and AC, respectively. We know that AB = a and AC = b.
1. Identify the Midpoints:
Let D be the midpoint of AB and E be the midpoint of AC. By the midpoint theorem, we know that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half its length.
2. Express DE in terms of BC:
According to the midpoint theorem, the length of DE is equal to half the length of BC:
DE=12BC
3. Determine the Length of BC:
To find BC, we can use the coordinates of points A, B, and C. Let's assume:
- A is at the origin (0, 0).
- B is at (a, 0).
- C is at (0, b).
Now we can find the coordinates of D and E:
- D, the midpoint of AB, has coordinates:
D=(0+a2,0+02)=(a2,0)
- E, the midpoint of AC, has coordinates:
E=(0+02,0+b2)=(0,b2)
4. Calculate the Length of DE:
Now, we can calculate the distance DE using the distance formula:
DE=√(a2−0)2+(0−b2)2
Simplifying this gives:
DE=√(a2)2+(−b2)2=√a24+b24=√a2+b24=12√a2+b2
5. Relate DE to BC:
Since we established that DE is half of BC, we can express BC in terms of a and b. The length of BC can be derived from the coordinates of B and C:
BC=√(a−0)2+(0−b)2=√a2+b2
Therefore, we have:
DE=12BC=12√a2+b2
6. Final Expression:
However, we need to express DE in the form provided in the options. Since DE is half the difference of the lengths of the sides:
DE=b2−a2
Thus, we arrive at:
DE=b−a2
This matches with option 4: b2−a2.
Conclusion:
The length of segment DE is given by:
DE=b2−a2
Thus, the answer is option 4.
Let D be the midpoint of AB and E be the midpoint of AC. By the midpoint theorem, we know that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half its length.
According to the midpoint theorem, the length of DE is equal to half the length of BC:
DE=12BC
To find BC, we can use the coordinates of points A, B, and C. Let's assume:
- A is at the origin (0, 0).
- B is at (a, 0).
- C is at (0, b).
- D, the midpoint of AB, has coordinates:
D=(0+a2,0+02)=(a2,0)
- E, the midpoint of AC, has coordinates:
E=(0+02,0+b2)=(0,b2)
Now, we can calculate the distance DE using the distance formula:
DE=√(a2−0)2+(0−b2)2
Simplifying this gives:
DE=√(a2)2+(−b2)2=√a24+b24=√a2+b24=12√a2+b2
Since we established that DE is half of BC, we can express BC in terms of a and b. The length of BC can be derived from the coordinates of B and C:
BC=√(a−0)2+(0−b)2=√a2+b2
Therefore, we have:
DE=12BC=12√a2+b2
However, we need to express DE in the form provided in the options. Since DE is half the difference of the lengths of the sides:
DE=b2−a2
Thus, we arrive at:
DE=b−a2
This matches with option 4: b2−a2.
The length of segment DE is given by:
DE=b2−a2
Thus, the answer is option 4.
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (More Than One Correct Option Type Questions)
7 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise (Statement I And Ii Type Questions)
3 Videos
- VECTOR ALGEBRABOOK - ARIHANT MATHSCHAPTER - VECTOR ALGEBRAEXERCISE - Exercise For Session 3
11 Videos
- TRIGONOMETRIC FUNCTIONS AND IDENTITIESBOOK - ARIHANT MATHSCHAPTER - TRIGONOMETRIC FUNCTIONS AND IDENTITIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
19 Videos
Similar Questions
Knowledge Check
Given an equilateral triangle ABC, D, E and F are the mid-points of the sides AB, BC and AC respectively, then the quadrilateral BEFD is exactly a
AsquareBrectangleCparallelogramDrhombusIn a triangle ABC, D, E, F are the mid-points of the sides BC, CA and AB respectively , the vector →AD is equal to
A→BE+→CFB→BE−→CFC→CF−→BED−→BE−→CFIn the adjoining figure, ABC is an isosceles triangle in which AB=AC. If E and F be the midpoints of AC and AB respectively, then
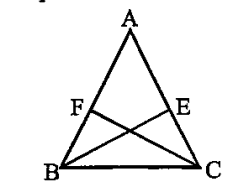ABE=CFB∠BFC=∠CEBCBF=CEDAll of these
ABC is an isosceles triangle in which AB=AC. If DandE are the mid-points of ABandAC respectively, prove that the points B,C,DandE are concylic.
View SolutionABC is an isosceles triangle in which AB=AC. If D and E are the mid-points of AB and AC respectively, prove that the points B, C, D and E are concyclic.
View SolutionLet ABC be an isosceles triangle with AB=AC and let D,E,F be the mid-points of BC,CA and AB respectively. Show that AD⊥FE and AD is bisected by FE.
"
View SolutionIn △ABC ,D and E are the points on sides AB and AC, respectively, such that DE || AC. If AD : DB = 5:3 then what is the ratio of the area of △BDE to that of the trapezium ACED ?/
त्रिभुज ABC में, D तथा E क्रमशः भुजा AB और BC पर स्थित ऐसे बिंदु हैं कि DE || AC है | यदि AD : DB = 5 : 3 है, तो त्रिभुज BDE के क्षेत्रफल और समलम्ब ACED के क्षेत्रफल में अनुपात ज्ञात करें |
View SolutionD and E are the mid-points of the sides AB and AC of ΔABC and O is any point on side BC. O is joined to A. If P and Q are the mid-points of OB and OC respectively, then DEQP is
View Solution