In the $△ O A B$ , M is the midpoint of AB, C is a point on OM, such that $2 O C = C M$ . X is a point on the side OB such that OX = 2XB. The line XC is produced to meet OA in Y. Then $\frac{O Y}{Y A} =$

A

$\frac{1}{3}$

B

$\frac{2}{7}$

C

$\frac{3}{2}$

D

$\frac{2}{5}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

$O A = a, B C = b$
$∴ O M = \frac{a + b}{2}$
$∴ O C = \frac{a + b}{6}$
$O X = \frac{2}{3} b$
Let $\frac{O Y}{Y A} = λ$
$∴ O Y = \frac{λ}{λ + 1} a$
Now points, Y,C and X are collinear.
$∴ Y C = m C X$
$∴ \frac{a + b}{6} - \frac{λ}{λ + 1} a = m \frac{2 b}{3} - m \frac{a + b}{6}$
Comparing coefficients of a and b
$∴ \frac{1}{6} - \frac{1}{λ + 1} = - \frac{m}{6}$
and $\frac{1}{6} = \frac{2 m}{3} - \frac{m}{6}$
$∴ m = \frac{1}{3} and λ = \frac{2}{7}$ .

|

Updated on:21/07/2023

Class 12 MATHS VECTOR ALGEBRA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In a triangle OAB, E is the midpoint of OB and D is a point on AB such that $A D : D B = 2 : 1$ . IF OD and AE intersects at P, then ratio of $\frac{O P}{P D}$ is equal to
A $3 : 2$
B $2 : 3$
C $3 : 4$
D $4 : 3$
Question 2 - Select One
In right triangle ABC, right angle at C, M is the mid-point of the hydrotenuse AB. C is joined to M and produced to a point D such that $D M = C M$ . Point D is joined to point B. Show that
(i) $Δ A M C ≅ Δ B M D$ (ii) $∠ D B C = ∠ A C B$
(iii) $Δ D B C ≅ Δ A C B$ (iv) $C M = \frac{1}{2} A B$

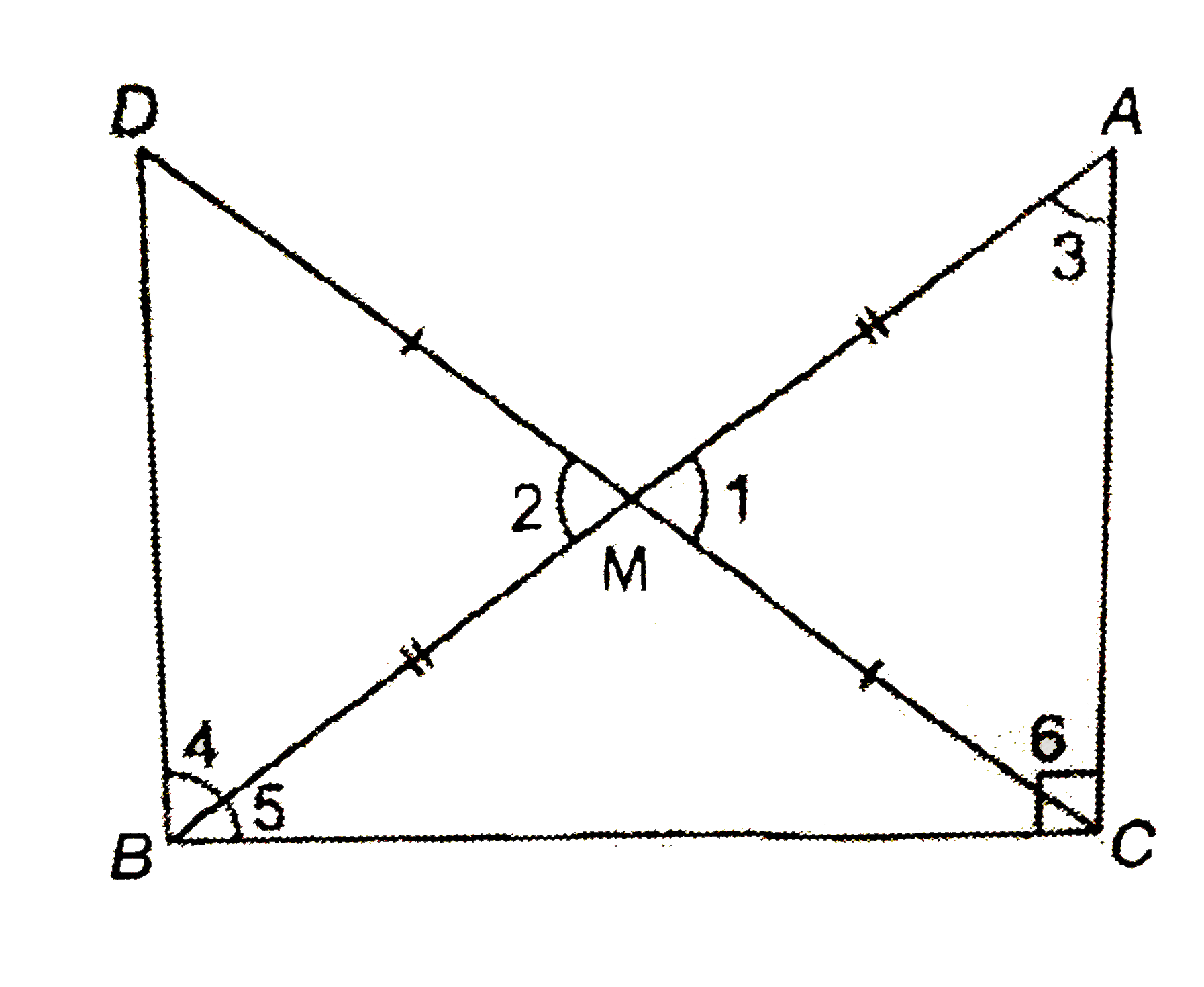AASA
BRHS
CSSS
DSAS
Question 3 - Select One
Let X be the midpoint of the side AB of triangle ABC. And Y be the mid point of CX. If Z is the point where BY meets the side AC, then $A Z : Z C$ is equal to
A $1 : 1$
B $2 : 1$
C $3 : 1$
D $3 : 2$

ARIHANT MATHS-VECTOR ALGEBRA-Exercise (Single Option Correct Type Questions)

Home
Ask Doubt
Profile