AB is a straight line and O is a point on AB, if a line OC is drawn not coinciding with OA or OB, then ∠AOC and ∠BOC are
equal
complementary
supplementary
together equal to 100
The correct Answer is:C
To solve the problem, we need to analyze the angles formed by the lines and points given in the question.
1. Identify the Points and Lines:
- We have a straight line AB.
- Point O is on line AB.
- Line OC is drawn such that it does not coincide with lines OA or OB.
2. Understanding the Angles:
- Since O is a point on the line AB, we can denote the angles formed by the lines as follows:
- Angle AOC is formed between line OA and line OC.
- Angle BOC is formed between line OB and line OC.
3. Analyzing the Angles:
- Since OC does not coincide with OA or OB, angles AOC and BOC are formed by the intersection of line OC with the lines OA and OB.
- The sum of angles around point O is 360 degrees.
4. Relationship Between Angles:
- The angles AOC and BOC are adjacent angles formed by the intersecting lines.
- Therefore, we can express the relationship between these angles:
- Angle AOC + Angle BOC + Angle AOB = 360 degrees.
- Since angle AOB is a straight line, it measures 180 degrees.
5. Final Relationship:
- Thus, we can conclude:
- Angle AOC + Angle BOC = 180 degrees.
Conclusion:
- Therefore, angles AOC and BOC are supplementary angles.
- We have a straight line AB.
- Point O is on line AB.
- Line OC is drawn such that it does not coincide with lines OA or OB.
- Since O is a point on the line AB, we can denote the angles formed by the lines as follows:
- Angle AOC is formed between line OA and line OC.
- Angle BOC is formed between line OB and line OC.
- Since OC does not coincide with OA or OB, angles AOC and BOC are formed by the intersection of line OC with the lines OA and OB.
- The sum of angles around point O is 360 degrees.
- The angles AOC and BOC are adjacent angles formed by the intersecting lines.
- Therefore, we can express the relationship between these angles:
- Angle AOC + Angle BOC + Angle AOB = 360 degrees.
- Since angle AOB is a straight line, it measures 180 degrees.
- Thus, we can conclude:
- Angle AOC + Angle BOC = 180 degrees.
- Therefore, angles AOC and BOC are supplementary angles.
Topper's Solved these Questions
Similar Questions
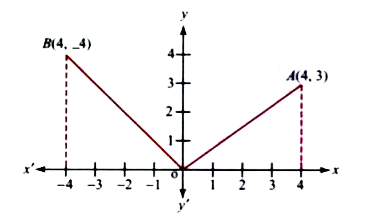
In the diagram, find the inclination of the line OB and also find the slope of the straight lines OA and OB.
View SolutionTwo straight lines AB and AC include an angle. A circle is drawn in this angle which touches both these lines. One more circle is drawn which touches both these lines as well as the previous circle. If the area of the bigger circle is 9 times the area of the smaller circle, then what must be the angle A ?
View Solution
Knowledge Check
AB is a straight line and O is a point on AB, if a line OC is drawn not coinciding with OA or OB, then ∠AOC and ∠BOC are
AequalBcomplementaryCsupplementaryDtogether equal to 100L M is a straight line and O is a point on LM .Line ON us drawn not coinciding with OL or OM .If ∠MON is three times ∠LON, then ∠MON is equal to :
A45∘B60∘C105∘D135∘AB is a straight line and O is a point lying on AB .A line OC is drawn from O such that ∠COA=36∘. OD is a line within ∠COA such that ∠DOA=13
∠COA . If OE is a line within the ∠BOC,∠BOE=14∠BOC , then ∠DOE must beA60∘B132∘C144∘D108∘
The line segments AB and CD intersect at O. OF is the internal bisector of obtuse angle BOC and OE is the internal bisector of acute angle AOC. If ∠BOC=130∘, what is the measure of ∠FOE?
View SolutionIn the given figure, AOB is a straight line and OC is a ray such that ∠AOC=(3x+20)∘ and ∠BOC=(2x−10)∘. Find the value of x and hence find (i) ∠AOC
(ii)∠BOC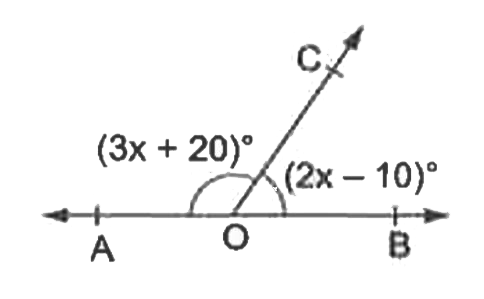
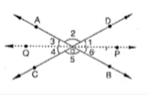
View SolutionIn figure, AB and CD are straight lines and OP and OQ are respectively the bisectors of angles ∠BOD and ∠AOC . Show that the rays OP and OQ are in the same line.
View SolutionIn the △OAB, M is the midpoint of AB, C is a point on OM, such that 2OC=CM. X is a point on the side OB such that OX = 2XB. The line XC is produced to meet OA in Y. Then OYYA=
View SolutionO is point on the line LM A line ON is drawn which is neither coincident with OL nor with OM if ∠MON is one third of ∠LON then ∠MON equal to
View Solution
